参考自：Dropout技术一览：可视化解释以及在DNN/CNN/RNN中的应用 (opens new window)

1. 动机

在深度机器学习中训练一个模型的主要挑战之一是协同适应。这意味着神经元是相互依赖的。他们对彼此的影响相当大，相对于他们的输入还不够独立。我们也经常发现一些神经元具有比其他神经元更重要的预测能力的情况。换句话说，我们会过度依赖于个别的神经元的输出。这些影响必须避免，权重必须具有一定的分布，以防止过拟合。某些神经元的协同适应和高预测能力可以通过不同的正则化方法进行调节。其中最常用的是 Dropout。然而，dropout 方法的全部功能很少被使用。取决于它是 DNN，一个 CNN 或一个 RNN，不同的 dropout 方法可以被应用。在实践中，我们只(或几乎)使用一个。我认为这是一个可怕的陷阱。所以在本文中，我们将从数学和可视化上深入到 dropouts 的世界中去理解：

• 标准的 Dropout 方法
• 标准 Dropout 的变体
• 用在 CNNs 上的 dropout 方法
• 用在 RNNs 上的 dropout 方法
• 其他的 dropout 应用(蒙特卡洛和压缩)

2. 符号

3. 各种各样的 Dropout

3.1 Standard dropout

最常用的 dropout 方法是 Hinton 等人在 2012 年推出的 Standard dropout。通常简单地称为 “Dropout”，在本文中我们将称之为 Standard dropout。

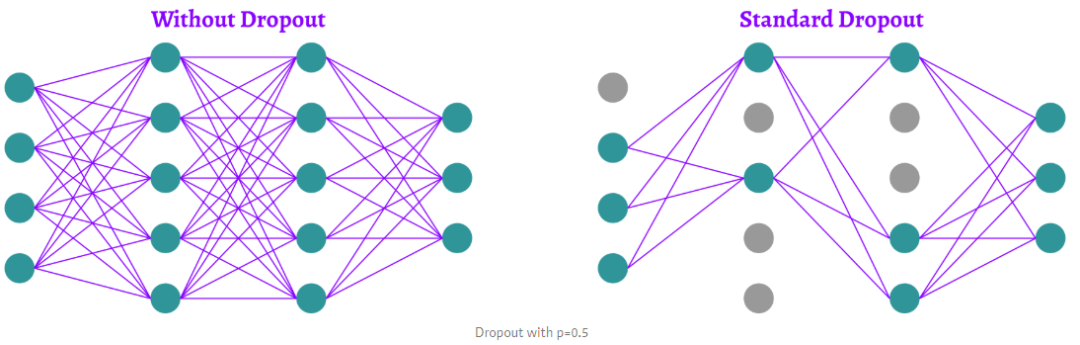
为了防止训练阶段的过拟合，随机去掉神经元。在一个密集的(或全连接的)网络中，对于每一层，我们给出了一个dropout的概率 p。在每次迭代中，每个神经元被去掉的概率为 p。Hinton等人的论文建议，输入层的dropout概率为“p=0.2”，隐藏层的dropout概率为“p=0.5”。显然，我们对输出层感兴趣，输出层是我们的预测结果。所以我们不会在输出层应用 dropout。

Dropout 具体使用的方法就是让被丢弃的值归 0，所以只需要创建一个元素值为 0 或 1 的 mask 与 feature vector 进行 element-wise product 即可。当某个 feature 归 0 后，与任何参数相乘都是 0，这也就相当于这部分网络不起作用了。

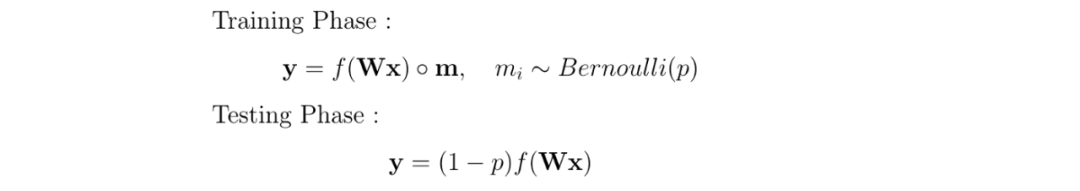
数学上，我们说每个神经元的丢弃概率遵循概率 p 的伯努利分布。因此，我们用一个 mask 对神经元向量(层)进行了一个元素级的操作，其中每个元素都是遵循伯努利分布的随机变量，取值 0 或 1。

在 testing 或 inference 阶段，没有 dropout，所有的神经元都是活跃的。为了补偿与训练阶段相比较的额外信息，我们用出现的概率来衡加权权重。所以神经元没有被忽略的概率，是“1 - p”。

一般我们会将dropout理解为“一种低成本的集成策略”，这是对的。具体过程大概可以这样理解。

经过上述置零操作后，我们可以认为 0 的那部分是被丢弃了，丢失了一部分信息。然而虽然信息丢失了，但生活还得继续呀，不对，是训练还得继续，所以就逼着模型用剩下的信息去拟合目标了。然而每次 dropout 是随机的，我们就不能侧重于某些节点了。所以总的来说就是——每次逼着模型用少量的特征学习，每次被学习的特征有不同，那么就是说，每个特征都应该对模型的预测有所贡献（而不是侧重部分特征，导致过拟合）。

最后预测的时候，就不 dropout 了，所以就等价于所有局部特征的平均（这次终于用上所有的信息了），理论上效果就变好了，过拟合也不严重了（因为风险平摊到了每个特征而不是部分特征上面）。

Standard Dropout 的实现伪代码如下：

def dropout(x, p):
    """
    x: feature vector
    p: 某个神经元被丢弃的概率，0 < p <=1
    """
    if 训练阶段:
        retain_prob = 1.0 - p
        sample = np.random.binomial(n=1, p=retain_prob, size=x.shape)  # 生成一个 0-1 分布的向量，形状与 x 一样
        x *= sample
        return x
    else:  # testing or inference 阶段
         x *= retain_prob
         return x

pytorch 使用 Dropout 的示例

import torch.nn as nn


input_size = 28 * 28   
hidden_size = 500   
num_classes = 10    


# 三层神经网络
class NeuralNet(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes):
        super(NeuralNet, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)  # 输入层到影藏层
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, num_classes)  # 影藏层到输出层
        self.dropout = nn.Dropout(p=0.5)  # dropout训练

    def forward(self, x):
        out = self.fc1(x)
        out = self.dropout(out)
        out = self.relu(out)
        out = self.fc2(out)
        return out
   

model = NeuralNet(input_size, hidden_size, num_classes)
model.train()
model.eval()

3.2 DropConnect

也许你已经熟悉标准的 Dropout 方法。但也有很多变化。要对密集网络的前向传递进行正则，可以在神经元上应用dropout。L. Wan等人介绍的 DropConnect 没有直接在神经元上应用 dropout，而是在连接这些神经元的权重和偏置上进行屏蔽与激活。

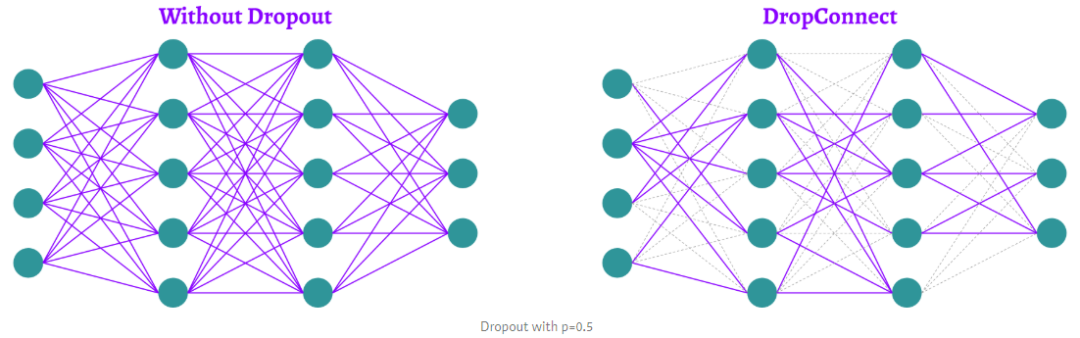
• Standard dropout 从特征的角度进行 drop，在反向传播时依然对所有权重都进行更新；
• DropConnect 对权重进行 drop，在反向传播过程中使用相应的 mask 屏蔽相应的权重，因此只对部分权重进行更新。

DropConnect 只能用于全连接层，原理如下：

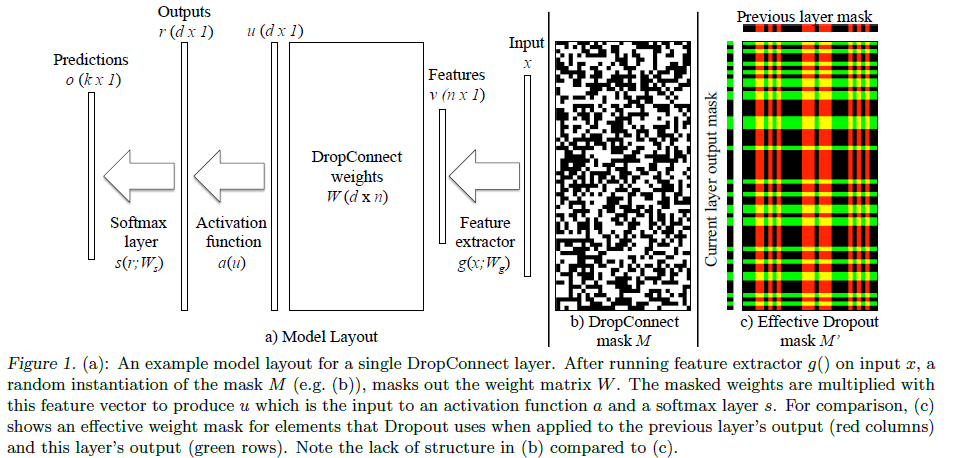
从上面的图中可以看到，一个含有 DropConnect 的 network 的运算过程如下：

• 输入 input
• 特征提取器从 input x 中提取 feature v
• 随机产生一个 0/1 的矩阵 mask，记为 M
• 使用 Mask 对权重 W 进行相乘得到 ，从而屏蔽掉某些权重
• 使用 与 feature v 进行矩阵相乘，得到 vector u，u 就是 activation function 的输入数据
• 经过 activation function 和 softmax 后得到预测值

加粗的步骤是 DropConnect 的特别之处，由此可见，DropConnect 就是在训练阶段通过对网络权重进行 mask 操作实现网络正则化。

DropConnect 的 inference 阶段中，需要对每个权重从一个 Gaussian 分布中进行 sample，算法如下（看不懂就算了）：

正是由于需要多次 sample，因此速度较慢，一般不会在产业中应用，这也是为何我们基本上没用过 DropConnect 的原因。

3.3 Standout

L. J. Ba 和 B. Frey 介绍的 Standout 旨在通过选择神经元来自适应地而不是随机地省略来改进标准的 dropout。 这是通过在控制神经网络结构的神经网络上叠加一个二元信念网络来实现的。 对于原始神经网络中的每个权重 ，Standout 在二元信念网络中添加一个相应的权重参数 ，并借助这个网络来生成一个 Bernoulli mask（我们将根据它们遵循的分布来命名这些 mask，这样会更简单）。在训练阶段，layer 的 output 由下式计算得出：

• 代表信念网络对该层的权重，g() 代表信念网络的激活函数。

虽然可以应用单独的学习算法来学习信念网络权重，但在实践中，作者发现这导致信念网络权重变得近似等于相应神经网络权重的仿射函数。 因此，确定信念网络权重的有效方法是将其设置为：

• 和 是常数

由此可以看到，权重 W 越大，神经元被丢弃的概率就越大。这有力地限制了某些神经元可能具有的高预测能力。

3.4 Gaussian Dropout