notebook
yubin
2022-12-21
目录

loss function

参考

# 1. loss function

损失函数（或称为代价函数）用来评估模型的预测值与真实值的差距，损失函数越小，模型的效果越好。损失函数是一个计算单个数值的函数，它指导模型学习，在学习过程将试图使其值最小化。

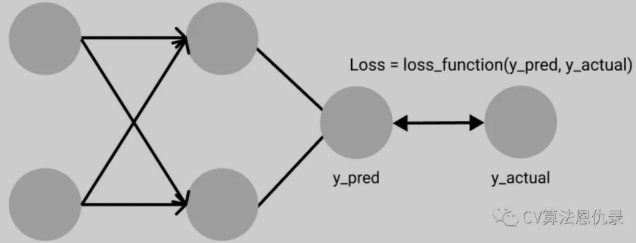
image-20221221141654184

常见的回归损失函数：L1 Loss、L2 Loss、Smooth L1 Loss

常见的分类损失函数：0-1 Loss、交叉熵、Negative Log-Likelihood Loss、Weighted Cross Entropy Loss 、Focal Loss

这些损失函数通过 torch.nn 库和 torch.nn.functional库导入。这两个库很类似，都涵盖了神经网络的各层操作，只是用法有点不同，nn 是类实现，nn.functional 是函数实现。nn.xxx 需要先实例化并传入参数，然后以函数调用的方式调用实例化的对象并传入输入数据。nn.functional.xxx 无需实例化，可直接使用。

# 2. 各种各样的 loss function

# 2.1 L1 Loss（Mean Absolute Error, MAE）

L1 损失函数计算预测张量中的每个值与真实值之间的平均绝对误差。它首先计算预测张量中的每个值与真实值之间的绝对差值，并计算所有绝对差值的总和。最后，它计算该和值的平均值以获得平均绝对误差（MAE）。L1 损失函数对于处理噪声非常鲁棒。

numpy 实现如下：

import numpy as np


y_pred = np.array([0.000, 0.100, 0.200])
y_true = np.array([0.000, 0.200, 0.250])
# Defining Mean Absolute Error loss function
def mae(pred, true):
    # Find absolute difference
    differences = pred - true
    absolute_differences = np.absolute(differences)
    # find the absoute mean
    mean_absolute_error = absolute_differences.mean()
    return mean_absolute_error
mae_value = mae(y_pred, y_true)
print ("MAE error is: " + str(mae_value))
# MAE error is: 0.049999999999999996
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

PyTorch 中的实现如下：

torch.nn.L1Loss：

import numpy as np
import torch
import torch.nn as nn


y_pred = np.array([0.000, 0.100, 0.200])
y_true = np.array([0.000, 0.200, 0.250])

MAE_Loss = nn.L1Loss() # 实例化
input = torch.tensor(y_pred)
target = torch.tensor(y_true)
output = MAE_Loss(input, target)
print(output)
1
2
3
4
5
6
7
8
9
10
11
12
13

torch.nn.functional.l1_loss：

import numpy as np
import torch
import torch.nn.functional as F

y_pred = np.array([0.000, 0.100, 0.200])
y_true = np.array([0.000, 0.200, 0.250])

input = torch.tensor(y_pred)
target = torch.tensor(y_true)
output = F.l1_loss(input, target)
print(output)
1
2
3
4
5
6
7
8
9
10
11

# 2.2 L2 Loss（Mean-Squared Error, MSE）

均方误差不是像平均绝对误差那样计算预测值和真实值之间的绝对差，而是计算平方差。这样做，相对较大的差异会受到更多的惩罚，而相对较小的差异则会受到更少的惩罚。然而，MSE 被认为在处理异常值和噪声方面不如 MAE 稳健。

PyTorch 中的 MSE 损失函数：

  • torch.nn.MSELoss
  • torch.nn.functional.mse_loss

# 2.3 Smooth L1 Loss

Smooth L1 损失函数通过结合了 MSE 和 MAE 的优点，来自 Fast R-CNN 论文。

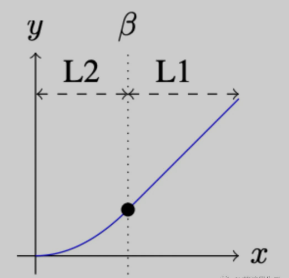
image-20221221145548969

当真实值和预测值之间的绝对差低于 时，使用 MSE 损失。MSE 损失曲线是一条连续曲线，这意味着每个损失值处的梯度都会变化，并且可以在任何地方可导。然而，对于非常大的损失值，梯度爆炸，使用 MAE，当绝对差变得大于 并且消除了潜在的梯度爆炸时，其梯度对于每个损失值几乎是恒定的。

PyTorch 使用示例：

  • torch.nn.SmoothL1Loss
  • torch.nn.functional.smooth_l1_loss
import torch


loss = torch.nn.SmoothL1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output1 = loss(input, target)
output2 = torch.nn.functional.smooth_l1_loss(input, target)

print('output1: ',output1)
print('output2: ',output2) 

# output1:  tensor(0.7812, grad_fn=<SmoothL1LossBackward0>)
# output2:  tensor(0.7812, grad_fn=<SmoothL1LossBackward0>)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 2.4 0-1 Loss

0-1 Loss 它直接比较预测值和真实值是否一致，不一致为 1，一致为 0。

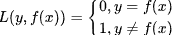
image-20221221150030008

其中，y 表示真实值，f(x) 表示预测值。0-1 Loss 本质是计算分类错误的个数，函数也不可导，在需要反向传播的学习任务中，无法被使用。

# 2.5 Cross-Entropy Loss

Cross-Entropy（交叉熵）是理解分类损失函数的基础，给定两个离散分布 y 和 f(x)，交叉熵的公式如下：

可以近似将交叉熵理解为衡量两个分布的距离，假设两个分布 y 表示真实值，f(x) 表示预测值，通过优化模型参数，降低 y 和 f(x) 之间的距离，当距离趋近 0，预测值也在逼近真实值。

通常，当使用交叉熵损失时，我们的网络的输出是 softmax 层，这确保了神经网络的输出为概率值（介于0-1之间的值）。

PyTorch 使用示例：

  • torch.nn.CrossEntropy
  • torch.nn.functional.cross_entropy
loss = torch.nn.CrossEntropyLoss()
inputs = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output1 = loss(inputs, target)
output2 = torch.nn.functional.cross_entropy(inputs, target)

print('output1: ',output1)
print('output2: ',output2) 
# output1:  tensor(1.4797, grad_fn=<NllLossBackward0>)
# output2:  tensor(1.4797, grad_fn=<NllLossBackward0>)
1
2
3
4
5
6
7
8
9
10

请注意，打印输出中的梯度函数 grad_fn=<NllLossBackward0> 是负对数似然损失（NLL）。这实际上揭示了交叉熵损失将负对数似然损失与 log-softmax 层相结合。

# 2.6 Negative Log-Likelihood Loss（NLL）

Negative Log-Likelihood (NLL) 损失函数的工作原理与交叉熵损失函数非常相似。表达式如下：

应用场景：多分类问题

注：NLL 要求网络最后一层使用 softmax 作为激活函数。通过 softmax 将输出值映射为每个类别的概率值。

  • NLL 使用负号，因为概率（或似然）在 0 和 1 之间变化，并且此范围内的值的对数为负。最后，损失值变为正值。
  • 在 NLL 中，最小化损失函数有助于获得更好的输出。从近似最大似然估计 (MLE) 中检索负对数似然。这意味着尝试最大化模型的对数似然，从而最小化 NLL。

如前面在交叉熵部分所述，交叉熵损失结合了 log-softmax 层和 NLL 损失，以获得交叉熵损失的值。这意味着NLL损失可以通过使神经网络的最后一层是 log-softmax 而不是正常的 softmax 获得交叉熵损失值。

PyTorch 示例：

  • torch.nn.NLLLoss
  • torch.nn.functional.nll_loss
import torch.nn as nn
import torch.nn.functional as F

m = nn.LogSoftmax(dim=1)
loss = nn.NLLLoss()

# input is of size N x C = 3 x 5
inputs = torch.randn(3, 5, requires_grad=True)

# each element in target has to have 0 <= value < C
target = torch.tensor([1, 0, 4])

output1 = loss(m(inputs), target)
output2 = F.nll_loss(m(inputs), target)
 
print('output1: ',output1)
print('output2: ',output2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 2.7 Weighted Cross Entropy Loss

加权交叉熵损失（Weighted Cross Entropy Loss ）是给较少的类别加权重。公式如下：

其中 与 表示类别的权重，不同类别的权重和它们的数量成比例，比如一个类别 a 的数据有 20 个，另一个类别 b 的数据有 80 个，那么 a 的权重是 ，b 的权重就是 。

# 2.8 Focal Loss

出自何凯明的《Focal Loss for Dense Object Detection》，Focal Loss 可以解决数据之间的样本不均衡和样本难易程度不一样。比如在病变图像的识别，一方面有病变的图片数量比较少，无病变的图片数量多；另一方面，有病变的图像中的病变区域占整张图片是比较小，特征难以学习，病变图片难以识别。

Focal Loss 在原始的 Cross Entropy Loss 上改进，先回顾一下 Cross Entropy Loss：

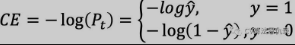
image-20221221153706627

为了解决数据不均衡，Focal Loss 添加权重 ，公式如下：

image-20221221153809528

Focal Loss 是对简单的数据添加一个小的权重，让损失函数更加关注困难的数据训练，即添加了 ，公式如下：

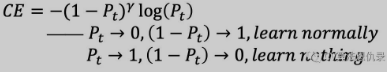
image-20221221154023030

这样二分类的 Focal Loss 表达式如下：

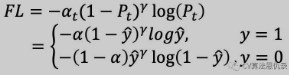
image-20221221154048809

多分类的 Focal Loss 表达式如下：

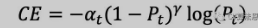
image-20221221154102199

  • 参数 和 分别用于控制正/负样本的比例，其取值范围为[0, 1]。 的取值一般可通过交叉验证来选择合适的值。
  • 参数 称为聚焦参数，其取值范围为 ，目的是通过减少易分类样本的权重，从而使模型在训练时更专注于困难样本。当 时，Focal Loss 就退化为交叉熵损失， 越大，对易分类样本的惩罚力度就越大。

PyTorch 自定义 Focal Loss 损失函数的示例如下：

import torch
import torch.nn as nn
import torch.nn.functional as F


class FocalLoss(nn.Module):
    def __init__(self, weight=None, gamma=2., reduction='none'):
        nn.Module.__init__(self)
        self.weight = weight
        self.gamma = gamma
        self.reduction = reduction
    
    def forward(self, input_tensor, target_tensor):
        log_prob = F.log_softmax(input_tensor, dim=-1)
        prob = torch.exp(log_prob)
        return F.nll_loss(
            ((1 - prob) ** self.gamma) * log_prob,
            target_tensor,
            weight=self.weight,
            reduction=self.reduction
        )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

使用自定义的损失函数：

weights = torch.ones(7)
loss = FocalLoss(gamma=2, weight=weights)
inputs = torch.randn(3, 7, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(7)
print('inputs:', inputs)
print('target:', target)
output = loss(inputs, target)
print('output:', output)
1
2
3
4
5
6
7
8

结果如下：

inputs: tensor([[ 0.5688, -1.1567,  1.8231, -0.2724, -1.2335,  0.9968,  0.9643],
        [-0.1824,  0.3010,  1.7070,  0.8743,  0.4528,  1.4306, -2.3726],
        [-2.5052, -0.3744,  0.3718, -1.5129, -2.0459,  1.0374, -0.5433]],
       requires_grad=True)
target: tensor([6, 5, 1])
output: tensor([1.1599, 0.7283, 1.6924], grad_fn=<NllLossBackward0>)
1
2
3
4
5
6

# 2.9 Hinge Embedding

表达式：

  • 其中 y 为 1 或 -1

应用场景：分类问题，特别是在确定两个输入是否不同或相似时。学习非线性嵌入或半监督学习任务。

示例：

input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)

hinge_loss = torch.nn.HingeEmbeddingLoss()
output = hinge_loss(input, target)
1
2
3
4
5

# 2.10 Margin Ranking Loss

Margin Ranking Loss 计算一个标准来预测输入之间的相对距离。这与其他损失函数（如 MSE 或交叉熵）不同，后者学习直接从给定的输入集进行预测。

表达式：

  • 标签张量 y（包含 1 或 -1）。当 y == 1 时，第一个输入将被假定为更大的值。它将排名高于第二个输入。如果 y == -1，则第二个输入将排名更高。

应用场景：排名问题，或者 KRL 中也有使用它

input_one = torch.randn(3, requires_grad=True)
input_two = torch.randn(3, requires_grad=True)
target = torch.randn(3).sign()

ranking_loss = torch.nn.MarginRankingLoss()
output = ranking_loss(input_one, input_two, target)
1
2
3
4
5
6

# 2.11 Triplet Margin Loss

计算一组 anchor（a）、positive-sample（p） 和 negative-sample（n） 的损失。

表达式：

应用场景：确定样本之间的相对相似性、用于基于内容的检索问题

示例：

anchor = torch.randn(100, 128, requires_grad=True)
positive = torch.randn(100, 128, requires_grad=True)
negative = torch.randn(100, 128, requires_grad=True)

triplet_margin_loss = torch.nn.TripletMarginLoss(margin=1.0, p=2)
output = triplet_margin_loss(anchor, positive, negative)
1
2
3
4
5
6

# 2.12 KL Divergence Loss

计算两个概率分布之间的差异。

表达式：

输出表示两个概率分布的接近程度。如果预测的概率分布与真实的概率分布相差很远，就会导致很大的损失。如果 KL Divergence 的值为零，则表示概率分布相同。

KL Divergence 与交叉熵损失的关键区别在于它们如何处理预测概率和实际概率。交叉熵根据预测的置信度惩罚模型，而 KL Divergence 则没有。KL Divergence 仅评估概率分布预测与 ground truth 分布的不同之处。

应用场景：逼近复杂函数多类分类任务确保预测的分布与训练数据的分布相似

示例：

input = torch.randn(2, 3, requires_grad=True)
target = torch.randn(2, 3)

kl_loss = torch.nn.KLDivLoss(reduction = 'batchmean')
output = kl_loss(input, target)
1
2
3
4
5
编辑 (opens new window)
上次更新: 2023/01/03, 05:28:25
学习率调度器
torch.nn 之 Module、ModuleList 和 Sequential

← torch.nn 之 Module、ModuleList 和 Sequential→

最近更新
01
Deep Reinforcement Learning
10-03
02
误删数据后怎么办
04-06
03
MySQL 一主多从
03-22
更多文章>
Theme by Vdoing | Copyright © 2021-2024 yubincloud | MIT License
×