1. Tensor

可参见官网，这里只介绍一些较不熟悉的部分。

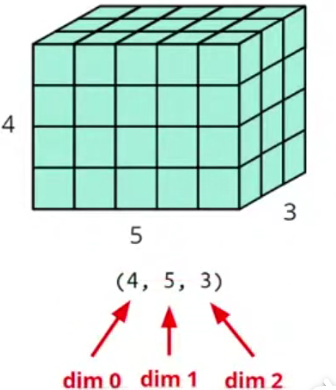
shape

dim in PyTorch == axis in NumPy

Operators

● Squeeze

Squeeze: remove the specified dimension with length = 1.

• 如果传给 squueeze 的 dim 在矩阵上 length ≠ 1，那么不会做任何改变。

● Unsqueeze

Unsqueeze: expand a new dimension.

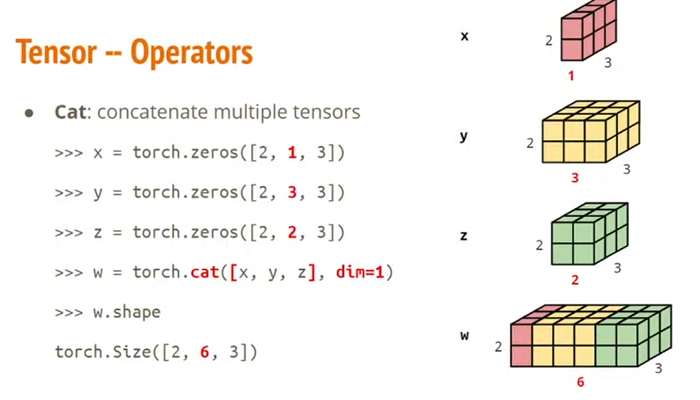
● Cat

Cat: concatenate multiple tensors.

2. Autograd

Autograd 中文是自动微分，是神经网络优化的核心。

2.1 微分示例

假设一个向量 作为输入，乘以 4 得到向量 ，最后求其长度得到标量 ，值为 5.6569，这个计算过程如下：

因此 关于 的微分是：

当输入和计算变得更为复杂时，PyTorch 的 Autograd 技术就可以帮助我们自动去求这些微分值。

2.2 基本原理

上面的计算过程中，、 和 都被当做节点，运行过程被抽象为信息流，复杂的计算也可以被抽象成一张计算图：

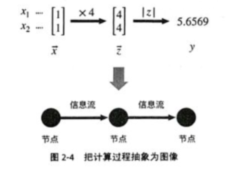
• 在计算图中，往往是节点代表运算（如加法或矩阵乘），箭头代表传输的值。

微分示例中， 是叶子节点， 是中间节点， 是输出节点，他们三者都是 Tensor。

计算图：绿色是叶子节点，橙色是中间节点，红色是输出节点，蓝色箭头表示信息流

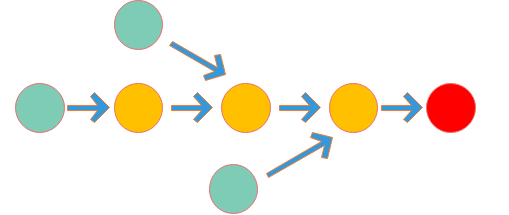
Tensor 在自动微分方面有三个重要属性：

• requires_grad：一个布尔值，默认 False，当其为 True 时表示该 Tensor 需要自动微分
• grad：用于存储 Tensor 的微分值
• grad_fn：用于存储 Tensor 的微分函数

当叶子节点的 requires_grad 为 True 时，信息流经过该节点时，所有中间节点的 requires_grad 属性都会变成 True，只要在输出节点调用反向传播函数 backward()，PyTorch 就会自动求出叶子节点的微分值并更新存储在叶子节点的 grad 属性。注意，只有叶子节点的 grad 属性能被更新。

2.3 前向传播

Autograd 技术可以帮助我们从叶子节点开始追踪信息流，记下整个过程使用的函数，知道输出节点，这个过程被称为前向传播。

首先初始化叶子节点 ：

x = torch.one(2)
x.requires_grad

打印出 False，因为默认情况下 Tensor 的 requires_grad 为 False。为了让 PyTorch 帮我们自动求微分，我们需要将其设为 True：

>>> X.requires_grad = True
>>> X
tensor([1., 1.], requires_grad=True)

此时 的 grad 和 grad_fn 属性为空。接下来我们计算 ：

>>> z = 4 * X
>>> z
tensor([4., 4.], grad_fn=<MulBackward0>)

这里面的 grad_fn 是微分函数，在此处是乘法的反向函数。最后我们用 norm() 函数求其长度得到 y：

>>> y = z.norm()
>>> y
tensor(5.6569, grad_fn=<CopyBackwards>)

2.4 反向传播

接下来，调用输出节点的 backward() 函数对整个图进行反向传播，求出微分值：

>>> y.backward()
>>> X.grad
tensor([2.8284, 2.8284])

运行后可以发现 的 grad 属性更新为 的微分值，这个结果与我们人工计算的结果一致。

再查看一下 和 的 grad 值，发现并没有改变，因为他们都不是叶子节点：

>>> z.grad
>>> y.grad

2.5 实例演示

假设我们要训练一个线性回归模型：，即输入是 ，输出是 ，真正的值是 ；

又令损失函数是 ，那么当输入一个 后，梯度的求法为：

求得损失值对于各参数的梯度后，便可以优化参数，设学习率为 ：

以上便模拟了一个深度学习的计算过程。

3. 线性回归

本节我们将实现一个线性回归（LR）模型。

3.1 理论分析

1）准备数据

import torch
import matplotlib.pyplot as plt

x = torch.Tensor([1.4, 5, 11, 16, 21])
y = torch.Tensor([14.4, 29.6, 62, 85, 113.4])

plt.scatter(x.numpy(), y.numpy())
plt.show()

得到图：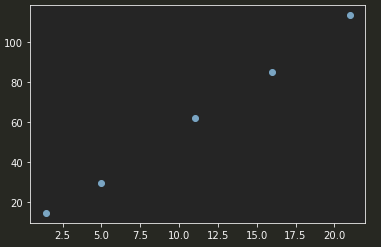

2）目标函数

因为我们假设用一条直线去拟合，所以可以假设该函数为：。我们的目标就是找到一组合适的 。

我们把上面 y 改写一下得到：，这样 是由样本中的 传入线性模型后计算得到的输出， 是我们真实样本值。因为测量会产生误差，我们用一个函数来衡量 和 之间的误差，这个函数就是损失函数。在这里，我们采用的损失函数是均方误差函数（Mean-Square Error，MSE）：

因此，我们的目标就是找一组合适的 使得损失函数的 L 值最小。

3）优化

为了让损失函数值 L 降到最小，我们就要开始调整参数 的值了！这个过程被称为优化。这里我们采用一种梯度下降的方法来寻找这个函数的最小值。

L 的梯度是：

这样优化的过程就是做这样的运算：，其中 是学习率。

4）批量输入

上面的表达式是一次一个样本的形式，在实际的优化中，我们是让多个样本同时在一个公式中出现，所有公式中的 和 都要增加一个维度， 升级为矩阵 ， 升级为 ，最终结果为：

损失函数 L 可以表示为：

5）训练

训练就是不断地通过前向传播和反向传播，对参数 进行调优，最终让损失函数的损失值 L 达到最小的过程：

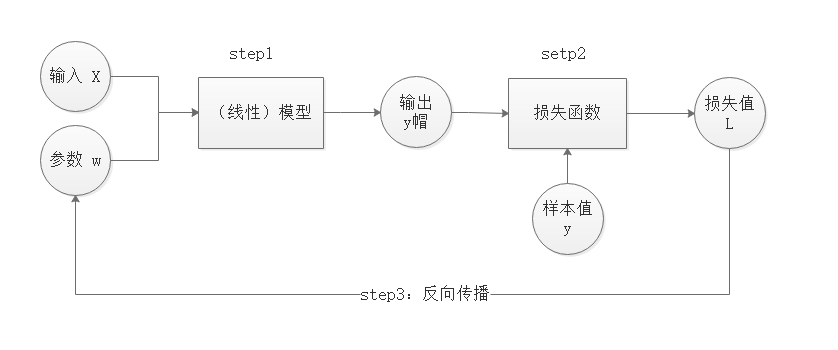
3.2 代码实现

1）准备数据

x，y 仍然使用我们之前的数据，我们首先对输入变量和各参数进行初始化：

import torch
import matplotlib.pyplot as plt

# 准备数据

# 生成矩阵X
def Produce_X(x):
	x0 = torch.ones(x.numpy().size) # 用ones产生初始值为1，大小与x相同的向量
	X = torch.stack((x,x0),dim=1)   # stack函数将两个向量拼合
	return X


x = torch.Tensor([1.4,5,11,16,21])
y = torch.Tensor([14.4,29.6,62,85.5,113.4])
X = Produce_X(x)

# 定义权重w的变量
w = torch.rand(2,requires_grad=True)

inputs = X 
target = y

• Produce_X 函数将 x 与一个与之相同形状的全 1 向量进行合并得到一个 X，它的实际数据如下：

  tensor([[ 1.4000,  1.0000],
          [ 5.0000,  1.0000],
          [11.0000,  1.0000],
          [16.0000,  1.0000],
          [21.0000,  1.0000]])
  

  这样 X 与 的乘积便相当于一个 。

• 用 rand() 函数来初始化参数向量 ，根据 Autograd 中所介绍的，参数 w 属于计算图的叶子节点，需要进行自动微分并利用梯度下降来更新，因此需要专门将 w 的 requires_grad 设置为 True。

2）训练

每一轮的训练分成两部分：前向传播和反向传播

#训练
def train(epochs=1,learning_rate=0.01):
	for epoch in range(epochs):

		#前向传播
		output = inputs.mv(w) #公式：y=Xw
		loss = (output - target).pow(2).sum() # 公式：L = ∑(y-y')^2

		#反向传播
		loss.backward() 
		w.data -= learning_rate * w.grad  # 更新权重w，公式：w_(t+1)= w_(t) - 𝜼*▽J
		
		w.grad.zero_() # 清空grad的值

		if epoch % 80 == 0:
			draw(output,loss)

	#plt.savefig('plot1.png', format='png')

	return w, loss

• 注意，我们更新完 w 后，必须清空 w 的 grad 的值，否则 grad 的值会持续累加。所以，这里使用 zero_() 函数来清空梯度值。

为了能够观察到训练的变化，我们可以让程序每进行 80 次循环就更新一次图像，于是定义一个 draw() 函数：

#绘图
def draw(output,loss):
	plt.cla() # 清空函数图像
	plt.scatter(x.numpy(), y.numpy()) # 绘制散点图
	
	plt.plot(x.numpy(), output.data.numpy(),'r-', lw=5) # 绘制出回归直线
	plt.text(0.5, 0,'Loss=%s' % (loss.item()),fontdict={'size':20,'color':'red'})
	#plt.text(3, 9,'Loss=%s' % (loss.item()),fontdict={'size':20,'color':'red'})
	#plt.axis([10, 160, 0, 0.03])

	plt.pause(0.005)

于是便可以训练了：

w, loss = train(10000,learning_rate = 1e-4)  #学习率设置为1x10^(-4)

训练完之后打印最终结果：

print("final loss:", loss.item())
print("weights:", w.data)

运行结果：

final loss: 8.2430419921875
weights: tensor([5.0840, 5.5849])

3.3 大规模数据集实例

之前训练时我们将 5 个数据样本同时输入程序，这种方式叫做批输入，这种方式是快速而有效的。

人们通过对神经元的研究，对其进行数学抽象得到了人工神经元模型：

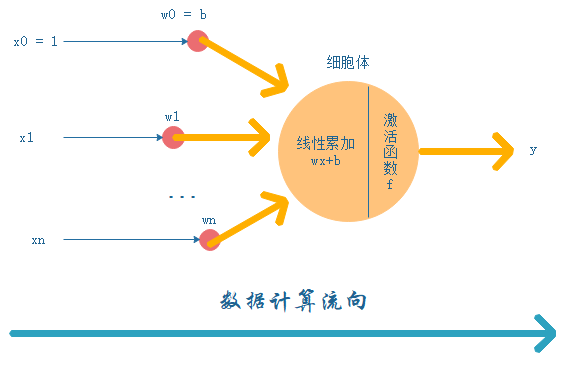
PyTorch 为我们预先编写好了损失函数和优化函数等，我们将代码再重新编写一次：

1）准备数据

import torch
import matplotlib.pyplot as plt
from torch import nn, optim
from time import perf_counter

# 用linspace产生（-3，3）区间内的100000个点，并使用unsqueeze函数增加一个维度
x = torch.unsqueeze(torch.linspace(-3,3,100000),dim=1)

# 假设真实函数是y=x，我们在上面增加一些误差，更加符合实际情况
y = x + 1.2 * torch.rand(x.size())

2）定义模型

定义一个线性回归的模型 LR，它继承自 nn.Module，并在其中使用 nn.Linear() 构造线性模型：

class LR(nn.Module):
    def __init__(self):
        super(LR,self).__init__()
        self.linear = nn.Linear(1,1)

    def forward(self,x):
        out = self.linear(x)
        return out

• nn.Linear() 的第一个参数代表输入数据的维度，第二个参数代表输出数据的维度。这里 x 和 y 都是一维的，因此设置为 nn.Linear(1, 1)。
• forward() 函数来构造神经网络前向传播的计算步骤。

3）实例化模型

如果平台支持 CUDA，实例化 LR 类后需要调用 cuda() 方法：

#如果支持CUDA，则采用CUDA加速
CUDA = torch.cuda.is_available()

if CUDA:
	LR_model = LR().cuda()
	inputs = x.cuda()
	target = y.cuda()
else:
	LR_model = LR()
	inputs = x
	target = y

4）损失函数

nn 模块中预设有均方误差函数：

criterion = nn.MSELoss()

5）优化器

下面采用“随机梯度下降”的方法来更新权重。随机梯度下降实际上就是梯度下降法的改良版，不采用梯度下降法中把全部数据拿来计算梯度的方法，而是每次随机挑选一个数据样本计算梯度值，并进行权值更新。这样做的好处是可以避免一次性加载全部数据导致的内存溢出问题，还可以防止优化的时候陷入局部最小值。这里我们使用 PyTorch 预设的随机梯度下降函数 SGD() 进行更新：

optimizer = optim.SGD(LR_model.parameters(), lr=1e-4)

• SGD() 函数的第一个参数是需要优化的神经网络模型的参数，第二个参数是学习率。

6）训练

开始编写 train() 函数，其参数依次是被训练的神经网络模型、损失函数、优化器和训练轮数：

def draw(output,loss):
    """可视化"""
    if CUDA:
        output = output.cpu()
    plt.cla()
    plt.scatter(x.numpy(), y.numpy())
    plt.plot(x.numpy(), output.data.numpy(),'r-', lw=5)
    plt.text(0.5,0,'Loss=%s' % (loss.item()),fontdict={'size':20,'color':'red'})
    plt.pause(0.005)

def train(model, criterion, optimizer, epochs):
    global loss
    for epoch in range(epochs):
        # forward
        output = model(inputs)
        loss = criterion(output,target)

        # backward
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()


        if epoch % 80 == 0:
            draw(output,loss)

    return model, loss

• 如果采用了 CUDA 加速，draw 函数的 output 需要还原成 CPU 的数据类型才能进行绘图
• 在前向传播阶段，我们将 inputs 输入神经网络模型 model 得到 output，接下来用定义的损失函数 criterion 来计算损失值。
• 在反向传播阶段，先用 optimizer.zero_grad() 清空权值的 grad 值，随后用 backward() 计算梯度，并用优化器 optimizer.stip() 函数进行权值更新。

接下来我们定义初试时间 start，并传入模型、损失函数、优化器以及训练轮数（10 000 次）：

start = perf_counter()
LR_model,loss = train(LR_model,criterion,optimizer,10000)
finish = perf_counter()
time = finish - start

print("计算时间:%s" % time)
print("final loss:",loss.item())
print("weights:",list(LR_model.parameters()))

代码的训练结果如下：

计算时间:164.62969759999942
final loss: 0.12093639373779297
weights: [Parameter containing:
tensor([[0.9995]], device='cuda:0', requires_grad=True), Parameter containing:
tensor([0.5632], device='cuda:0', requires_grad=True)]

4. 非线性回归

非线性就是说我们的拟合函数并非直线或者平面，而是更加复杂的曲线或曲面。

4.1 激活函数

在人工神经元图中的后半段还有一个激活函数 f，但我们之前讨论的线性回归忽略了它。在没有激活函数的情况下，多个神经元的堆叠相当于多个线性模型的叠加，从总体上看，其神经网络本质上还是个线性模型。激活函数的出现就是为了让神经网络可以拟合复杂的非线性函数。激活函数 f 实际上是一个非常简单的非线性函数，但只要多个带有激活函数的神经元组合在一起，就具有拟合复杂非线性函数的强大能力。

各类激活函数可以百度，这里我们一般使用 ReLU 函数。

ReLU 函数：（）

因此整个神经元的计算过程如下：

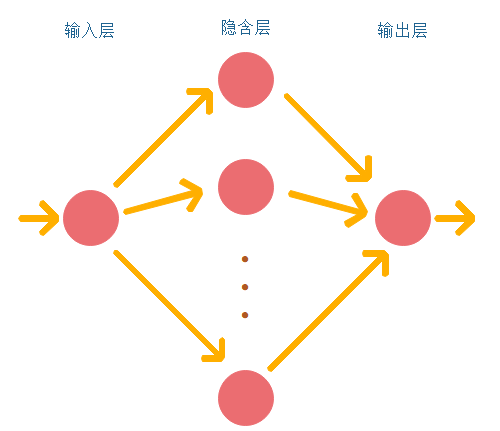
4.2 人工神经网络

为方便，我们可以将网络分成三层：输入层、隐含层（可以有多层）和输出层。隐含层的层数大于等于 2 的神经网络称之为深度神经网络。

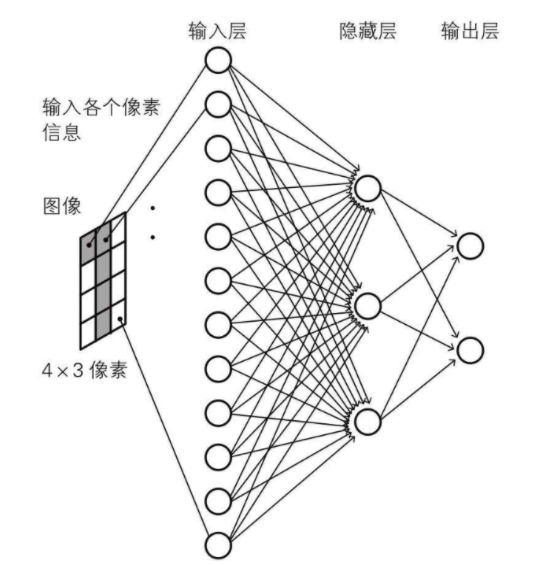
• 在这种示意图中，往往是用圆圈 ○ 表示神经元，用箭头表示它们的连接。此时，在箭头上有权重，这个权重和对应的神经元的值分别相乘，其和（严格来说，是经过激活函数变换后的值）作为下一个神经元的输入。

1）准备数据

我们根据一元三次方程自动生成一批数据样本，随后使用他们来演示神经网络的非线性回归：

import torch
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-3,3,10000),dim=1)
y = x.pow(3)+1.3*torch.rand(x.size())

plt.scatter(x.numpy(), y.numpy(),s=0.01)
plt.show()

2）建立模型

我们使用仅含有一层隐含层的神经网络来处理上面的数据：

from torch import nn,optim
import torch.nn.functional as F

class Net(nn.Module):  # 继承 torch.nn 的 Module
    def __init__(self, input_feature, num_hidden, outputs):
        super(Net, self).__init__()     # 继承 __init__ 
        # 定义每层神经元的结构与数目
        self.hidden = nn.Linear(input_feature, num_hidden)   # 线性隐含层
        self.out = nn.Linear(num_hidden, outputs)   # 输出层
 
    def forward(self, x):  
        # 前向传播输入值
        x = F.relu(self.hidden(x))      # 激励函数ReLU处理隐含层的输出
        x = self.out(x)             # 最终输出值
        return x

• 激活函数的使用直接调用 torch.nn.functional.F.relu 即可。

实例化 Net，设置输入为 1 维，隐含层节点数为 20，输出为 1 维：

CUDA = torch.cuda.is_available()

if CUDA:
	#初始化输入神经元数目为1，隐含层数目为20，输出神经元数目为1的神经网络模型
	net = Net(input_feature=1, num_hidden=20, outputs=1).cuda()
	inputs = x.cuda()
	target = y.cuda()
else:
	net = Net(input_feature=1, num_hidden=20, outputs=1)
	inputs = x
	target = y

与线性回归一样，优化器选择随机梯度下降，损失函数为均方误差：

optimizer = optim.SGD(net.parameters(), lr=0.01)  # 传入 net 的所有参数, 学习率
criterion = nn.MSELoss()      # 预测值和真实值的误差计算公式 (均方差)

3）训练

训练函数 train() 与之前类似，也是分成前向传播和反向传播两个步骤：

def draw(output,loss):
	if CUDA:
		output = output.cpu()
	plt.cla()
	plt.scatter(x.numpy(), y.numpy())
	plt.plot(x.numpy(), output.data.numpy(),'r-', lw=5)
	plt.text(-2,-20,'Loss=%s' % (loss.item()),fontdict={'size':20,'color':'red'})
	plt.pause(0.005)


def train(model,criterion,optimizer,epochs):
	for epoch in range(epochs):
		# forward
		output = model(inputs)
		loss = criterion(output,target)

		# backward
		optimizer.zero_grad()
		loss.backward()
		optimizer.step()
		
		if epoch % 80 == 0:
			draw(output,loss)

	return model,loss

我们训练 10000 次，并打印最终结果：

net,loss = train(net,criterion,optimizer,10000)

print("final loss:", loss.item())

5. 逻辑回归

线性回归和非线性回归的输出都是连续的，而逻辑回归的输出是二元离散的，即输出 y 只有两种结果，因此，逻辑回归也常常被当作二元分类问题。

5.1 sigmoid 函数

非线性 sigmoid 函数（常简写为 sigm）：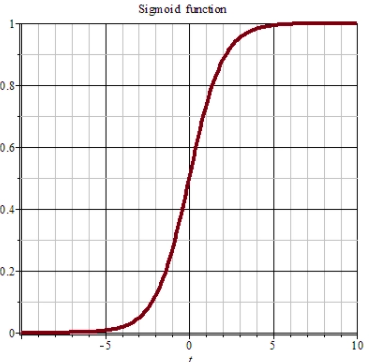

二元分类的模型结构如下：

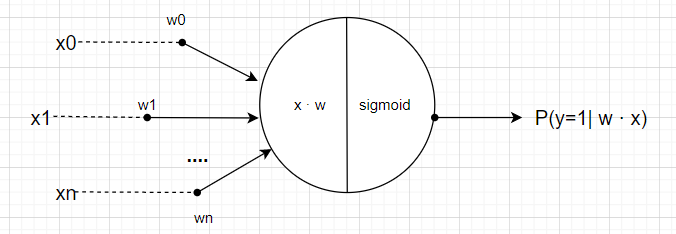
这样将输入 经过网络后，通过 映射为集合 （0， 1） 中的一个实数，我们可以将这个最终输出当作 y=1 的概率 。

sigmoid 已预置在 PyTorch 的 torch.sigmoid() 中，该函数可以将输入的 Tensor 输出成（0,1）之间的数，且和为 1：

>>> a = torch.randn(2)
>>> a
tensor([-0.2128,  0.5412])
>>> torch.sigmoid(a)
tensor([0.4470, 0.6321])

5.2 交叉熵损失函数

交叉熵损失函数是分类问题中常用的损失函数。在 PyTorch 中已经预置在 nn.CrossEntropyLoss() 中了。

为什么用交叉熵函数？我们可以将二元分类问题抽象成数学中的伯努利模型，然后对其使用最大似然法得到似然度的计算公式，通过对其进行转化，可以将求似然度的最大值转化为求一个损失函数的最小值，这里的损失函数便是交叉熵函数。

5.3 逻辑回归示例

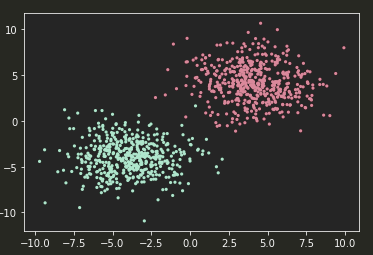
1）准备数据

import torch
import matplotlib.pyplot as plt
from torch import nn,optim

means = torch.ones(500, 2) #ones函数生成500x2的数据
data0 = torch.normal(4 * means, 2) #构造一个均值为4，标准差为2的数据簇
data1 = torch.normal(-4 * means, 2) #构造一个均值为-4，标准差为2的数据簇
label0 = torch.zeros(500) #500个标签0
label1 = torch.ones(500) #500个标签1

x = torch.cat((data0, data1), ).type(torch.FloatTensor) 
y = torch.cat((label0, label1), ).type(torch.LongTensor)

plt.scatter(x.numpy()[:,0], x.numpy()[:, 1], c=y.numpy(), s=10, lw=0, cmap='RdYlGn')
plt.show()

2）建立模型

class Net(nn.Module):     # 继承 torch 的 Module
    def __init__(self):
        super(Net, self).__init__()     # 继承 __init__ 功能
        self.linear = nn.Linear(2,2)

    def forward(self, x):
        x = self.linear(x)
        x = torch.sigmoid(x)
        return x

CUDA = torch.cuda.is_available()

if CUDA:
    net = Net().cuda()
    inputs = x.cuda()
    target = y.cuda()
else:
    net = Net()
    inputs = x
    target = y

• nn.Linear(2, 2) 的输入包括两个特征 ，分别代表横轴和纵轴；输出的是两个类“得分”情况，我们假设哪一类分数高，就属于哪一类。可以使用 sigmoid 函数来生成两个类的概率。

我们仍然使用随机梯度下降来优化，损失函数使用交叉熵函数：

optimizer = optim.SGD(net.parameters(), lr=0.02)
criterion = nn.CrossEntropyLoss()

3）训练

def draw(output):
    if CUDA:
        output=output.cpu()
    plt.cla()
    output = torch.max((output), 1)[1] 
    pred_y = output.data.numpy().squeeze()
    target_y = y.numpy()
    plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=pred_y, s=10, lw=0, cmap='RdYlGn')
    accuracy = sum(pred_y == target_y)/1000.0  
    plt.text(1.5, -4, 'Accuracy=%s' % (accuracy), fontdict={'size': 20, 'color':  'red'})
    plt.pause(0.1)


def train(model,criterion,optimizer,epochs):
    for epoch in range(epochs):
        #forward
        output = model(inputs)
        loss = criterion(output, target)

        #backward
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        if epoch % 40 == 0:
            draw(output)


train(net,criterion,optimizer,1000)

• 第 5 行的 torch.max() 会返回 output 中概率最大的一组数值与该类别的标签。

torch.max()

torch.max() 会返回选定维度中的最大值和序列号，例如 torch.max(b, 1) 会返回第一维的最大值和序列号：

>>> b = torch.randn(5, 2)
>>> b
tensor([[ 0.4022, -0.7402],
        [ 1.4084,  0.0899],
        [-1.5336,  0.8580],
        [ 0.7828, -0.5670],
        [-0.1495,  0.0716]])
>>> torch.max(b, 1)
torch.return_types.max(
values=tensor([0.4022, 1.4084, 0.8580, 0.7828, 0.0716]),
indices=tensor([0, 0, 1, 0, 1]))

6. 多元分类

逻辑回归是二元分类，属于多元分类的特殊情况。

6.1 softmax 函数

多元分类与二元分类类似，区别在于用 softmax 代替 sigmoid。多元分类的神经网络要求输出层的神经元数目与所需分类的类别数保持一致。softmax 能将所有分类的分数值 转化为概率 ，且各概率和为 1。

多元分类模型的结构：

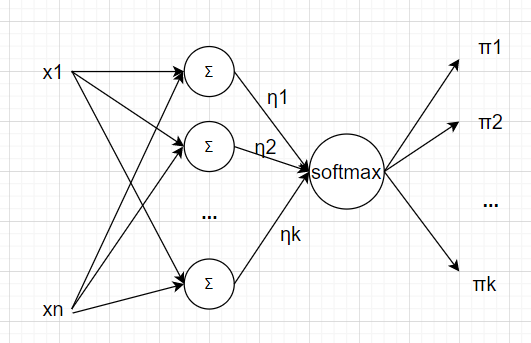
softmax 函数：

softmax 巧妙地将多个分类的分数转化为（0,1）的值并且和为 1：

6.2 多元分类示例

1）准备数据

import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F
from torch import nn,optim
 
# 生成数据
means = torch.ones(500, 2) 
data0 = torch.normal(4*means, 2)      
data1 = torch.normal(-4*means, 1)    
data2 = torch.normal(-8*means, 1)     
label0 = torch.zeros(500)
label1 = torch.ones(500)                
label2 = label1*2  #500个标签2
 
x = torch.cat((data0, data1, data2), ).type(torch.FloatTensor)  
y = torch.cat((label0, label1, label2), ).type(torch.LongTensor)    
 
plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=y.numpy(), s=10, lw=0, cmap='RdYlGn')
plt.show()

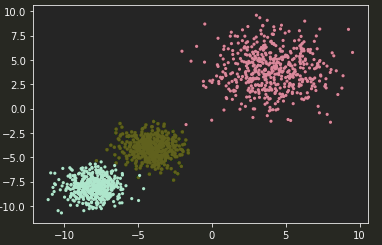
2）建立模型

class Net(nn.Module):    
    def __init__(self, input_feature, num_hidden,outputs):
        super(Net, self).__init__()     
        self.hidden = nn.Linear(input_feature, num_hidden)   # 线性隐含层
        self.out = nn.Linear(num_hidden, outputs)       # 输出层

    def forward(self, x):
        x = F.relu(self.hidden(x))      # 激励函数ReLU处理隐含层的输出
        x = self.out(x)
        x = F.softmax(x)     #使用softmax将输出层的数据转换成概率值           
        return x

CUDA = torch.cuda.is_available()

if CUDA:
    net = Net(input_feature=2, num_hidden=20,outputs=3).cuda()
    inputs = x.cuda()
    target = y.cuda()
else:
    net = Net(input_feature=2, num_hidden=20,outputs=3)
    inputs = x
    target = y

optimizer = optim.SGD(net.parameters(), lr=0.02)
criterion = nn.CrossEntropyLoss()

3）训练

ef draw(output):
    if CUDA:
        output=output.cpu()
    plt.cla()
    output = torch.max((output), 1)[1] 
    pred_y = output.data.numpy().squeeze()
    target_y = y.numpy()
    plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=pred_y, s=10, lw=0, cmap='RdYlGn')
    accuracy = sum(pred_y == target_y)/1500.0  
    plt.text(1.5, -4, 'Accuracy=%s' % (accuracy), fontdict={'size': 20, 'color':  'red'})
    plt.pause(0.1)

def train(model,criterion,optimizer,epochs):
    for epoch in range(epochs):
        #forward
        output = model(inputs)
        
        loss = criterion(output,target)

        #backward
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        if epoch % 40 == 0:
            draw(output)

train(net,criterion,optimizer,10000)

7. 卷积神经网络

7.1 引入卷积

经过对猫的脑皮层研究发现，视觉系统的信息处理是分级的。卷积神经网络模仿人脑的视觉处理机制，采用分级提取特征的原理，每一级的特征均由网络学习提取。

在前面介绍的神经网络中，输入层被描述为一列神经元。而在卷积神经网络里，我们把输入层看做二维的神经元，如果输入的是像素大小为 28 * 28 的图片，则可以看做 28 * 28 的二维神经元，它的每一个节点对应图片在这个像素点的灰度值。

在传统神经网络中，我们会把输入层的节点与隐含层的节点采用全连接，而在 CNN 中，我们采用“局部感知”的方法，即不再把输入层的每个节点都连接到隐含层的每一个神经元节点上，而是用一个局部感知域（过滤器）不断移动进行卷积：

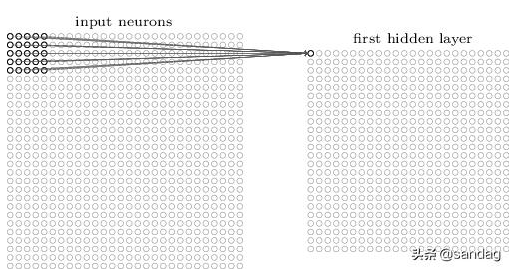
在卷积神经网络中，这种隐含层也被称为特征图。

为什么卷积？

在传统全连接的神经网络中，如果要对一张图片进行分类，连接方式如下图所示。我们把一张大小为 100×100 的图片的每个像素点都连接到每一个隐含层的节点上，如果隐含层的节点数为 10000，那么连接的权重总数则为 个。当图片像素更大，隐含层的节点数目更多时，则需要更加庞大的权重数目。

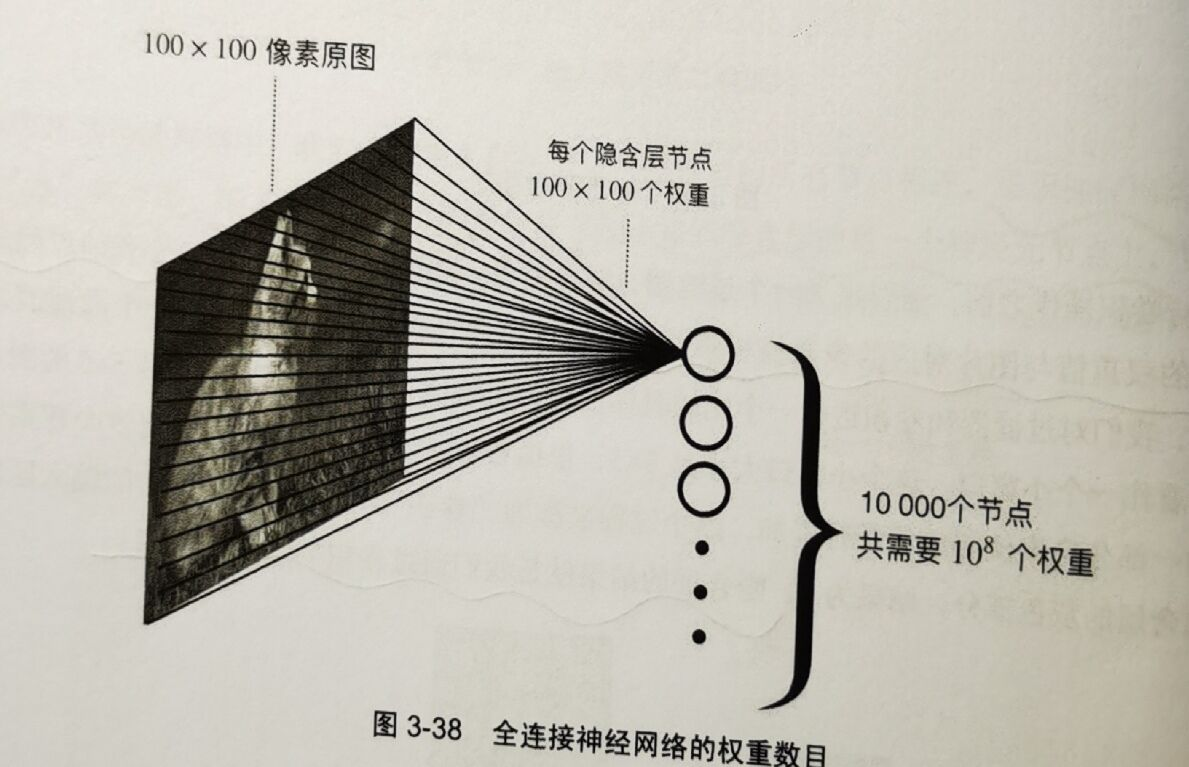
在卷积神经网络中，我们不再需要如此庞大的权重数目。，在利用 10×10 的过滤器对 100×100 的原图进行卷积时，该过滤器在不断滑动的过程中对应生成一张特征图，即一个过滤器(100个权重值)可对应一张特征图。如果我们有 100 张特征图，则一共只需要 104 个权重值。如此一来，在一个隐含层的情况下，卷积神经网络的权重数目可以减小至全连接神经网络权重数目的一万分之一，大大减少计算量，提高计算效率。

另外一个原因：想象一下，假设你想从一张图片中找到某个物体。 合理的假设是：无论哪种方法找到这个物体，都应该和物体的位置无关。 理想情况下，我们的系统应该能够利用常识：猪通常不在天上飞，飞机通常不在水里游泳。 但是，如果一只猪出现在图片顶部，我们还是应该认出它。 我们可以从儿童游戏”沃尔多在哪里”中得到灵感： 在这个游戏中包含了许多充斥着活动的混乱场景，而沃尔多通常潜伏在一些不太可能的位置，读者的目标就是找出他。 尽管沃尔多的装扮很有特点，但是在眼花缭乱的场景中找到他也如大海捞针。 然而沃尔多的样子并不取决于他潜藏的地方，因此我们可以使用一个“沃尔多检测器”扫描图像。 该检测器将图像分割成多个区域，并为每个区域包含沃尔多的可能性打分。 卷积神经网络正是将空间不变性（spatial invariance）的这一概念系统化，从而基于这个模型使用较少的参数来学习有用的表示。

现在，我们将上述想法总结一下，从而帮助我们设计适合于计算机视觉的神经网络架构：

1. 平移不变性（translation invariance）：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。
2. 局部性（locality）：神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。

进行卷积操作之前需要定义一个过滤器，其中每一格都有一个权重值。卷积的过程就是将格子中的权重值与图片对应的像素值相乘并累加。得到的隐含层的结果就是我们通过卷积生成的特征图：

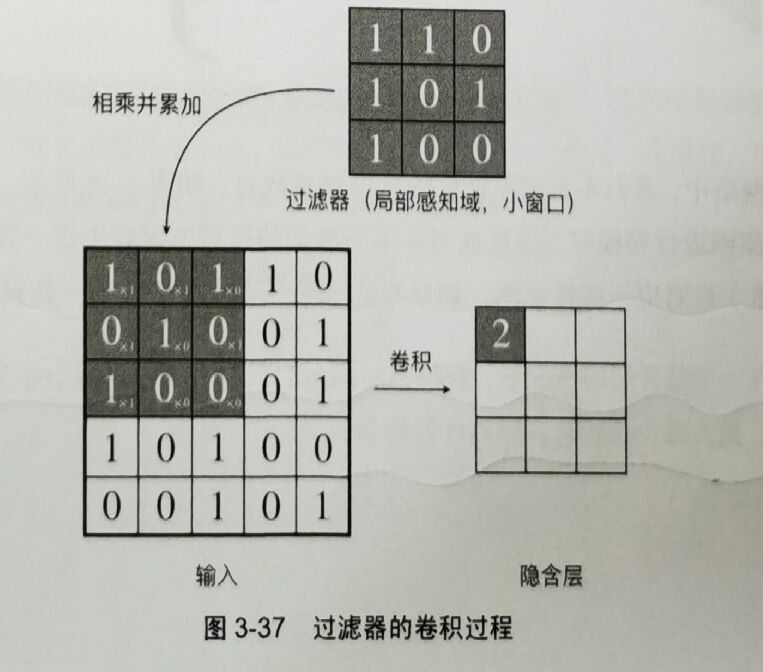
重要术语：卷积计算、过滤器（卷积核）、步长（stride）、填充（padding）

7.2 池化

池化的目的是降低数据的维度，过程实际上就是下采样：

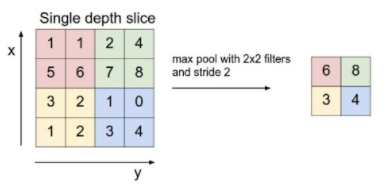
图示为最大池化，实际应用中生成池化特征的方式一般有两种：

• 最大值池化（Max-Pooling）：将池化窗口内的最大值作为池化结果的特征值
• 平均值池化（Mean-Pooling）：将池化窗口内的所有值的平均值作为池化结果的特征值