notebook
yubin
2021-10-24
目录

信息的处理与表示

# （一） 信息存储

# 1.1. 十六进制数

位权 16i

“十六进制 <=> 十进制” 的窍门： A-10 C-12 F-15

# 1.2. 进制转换

# 1.2.1. 二进制 <-> 十六进制

# 1.2.2. 十进制 <-> K 进制

# 整数的情况：

  1. 整数部分不断除以基数 K，并记下余数，直至商为 0 为止。
  2. 从最后一个余数起，逆向取各个余数，则为转换后的 K 进制数。

# 小数的情况：

乘以基数 K，记录整数部分，直至小数部分为 0 为止。

小数转换若无法乘到为 0，则选取一定精度（位数）。

# 1.2.3. K进制 <-> 十进制

按权展开

# 1.3. 编码

# 1.3.1. 编码长度

  • 字长 -> 指针的标称长度 -> 虚拟地址空间的最大大小

  • C 语言的 type size

# 1.3.2. 寻址与字节序

对于跨越多字节的 object，必须建立两个规律：① 这个 obj 的地址是什么？② 在内存中如何排列这些字节？

寻址：对象的地址为所使用字节中最小的地址

字节序：大端序与小端序

字节序变得重要的三个情况：

  1. 网络传输
  2. 阅读字节序列
  3. 当编写规避正常的类型系统程序时

# （二）位的运算

# 2.1. 布尔代数

  • & AND 与
  • | OR 或
  • ~ NOT 非
  • ^ XOR 异或

布尔环：长度为 w 的位向量上的 ^ & ~ 运算

布尔环中“加法”是 ^，其加法逆元是其本身，如 a ^ a = 0

应用于集合：|、& 对应于集合的并、交，~ 对应于补

# 2.2. C 语言的位级运算

& | ~ ^

# 2.2.1. 巧用异或

void inplace_swap(int* x, int* y) {
    *y = *x ^ *y;
    *x = *x ^ *y;
    *y = *x ^ *y;
}
1
2
3
4
5

注意

但该程序隐含是 x、y 不是同一个地址，否则 *x ^ *y 后直接全 0

# 2.2.2. 掩码运算

技巧：表达式 ~0 生成一个全1的掩码

# 2.3. 对比 C 语言的逻辑运算

&& || !

  • 运算结果为 0 或 1，大小为一个 byte
  • 具有短路求值（"提前终止"）的特性

# 2.4. C 语言的移位运算

# 左移

逻辑左移 x << k

# 右移

  • 逻辑右移：左边填 0
  • 算术右移：左边补 MST 的值

提示

C 语言未明确定义采用哪种

# （三）整数表示

# 3.1. 无符号数的编码

  • 编码具有唯一性

# 3.2. 补码编码

  • MST 的 称为符号位，权重
  • 取值范围：[, ]
  • 补码编码也具有唯一性
  • 两个值得注意的数学特性：
    1. 非对称：
    2. 最大值与无符号数的关系：

C 语言的常量声明：#include <limits.h>

# 3.3. 无符号数与有符号数之间的转换

强制类型转换的结果保持位值不变，只是改变了解释这些位的方式。

# （1）补码 -> 无符号数

  • 其实就是把符号位的权重由 逆转为

# （2）无符号数 -> 补码

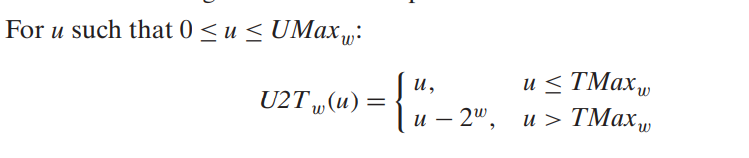
  • 其实就是将符号位的权重由 逆转为

# （3）C 语言类型转换产生的奇怪行为

expr 中有 signed 和 unsigned 混用时，有符号隐式地转换为无符号，包括比较运算符 < > == <= >=。

例如，-1 < 0U <=> 4294967295U < 0U => False

# （4）无符号与有符号转换的基本原则：

  1. 位模式不变
  2. 重新解读
  3. 会有意外的数值变化：被
  4. 表达式中混用时的隐式转换

# 3.4 扩展

扩展：不同字长之间的转换，同时又保持数值不变

  • 零扩展 -> 无符号数：前面填 0

  • 符号扩展 -> 有符号数：前面填 MSB 位（符号位）

当执行强制类型转换既涉及大小变化又涉及符号变化时，应该先改变大小再转变符号。 eg：short -> int -> unsigned int

# 3.5 截断

截断：减少表示一个数字的位数（如 int -> short）

基本原则：

  1. 无论是有符号数/无符号数，多出的位均被截断
  2. 结果重新解读

# （1）截断无符号数

w 位的 --截断--> k 位的

= mod , 其中 ,

# （2）截断有符号数

w 位的 --截断--> k 位的

, 其中 ,

提示

上面的过程就是按照 unsigned 解读位模式，截断至 k 位，即原 unsigned 值 mod

# 3.6 无符号数与有符号数的使用

隐式转换产生了很多 bug，除非已经知道隐含的转换规则，否则不要使用。

使用 unsigned 的两种情况：

  1. 进行模运算和多精度运算时（此时数字由字的数组表示）
  2. 用二进制位表示集合时

# （四）整数运算

# 4.1 无符号加法 UAdd

两个 w 位 unsigned 相加 -> 真实和需要 w+1 位 -> 丢弃进位，得到 w 位

模数加法：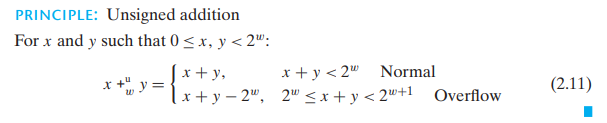

检测溢出：，当且仅当 （或） 时溢出。

# 4.2 补码加法 TAdd

TAdd 与 UAdd 有着完全相同的位级表现。

功能：

  1. 真实和需要 w+1 位
  2. 丢弃 MSB 位
  3. 将剩余位视为补码整数

补码加法：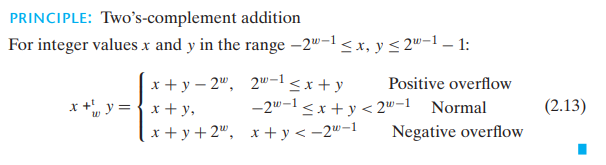

检测溢出：s = x + y，若 x > 0, y > 0 但 s <= 0，则正溢出；若 x < 0, y < 0 但 s >= 0，则负溢出。

# 4.3 阿贝尔群 Abelian Group

模数加法形成了阿贝尔群，表示为 <, +>.

特性：封闭性、交换性、结合性、单位元 0、有加法逆元（ 与 ）

TAdd 与带 UAdd 加法的无符号数是同构群（因为有着相同的位模式）

补码加法也构成一个群：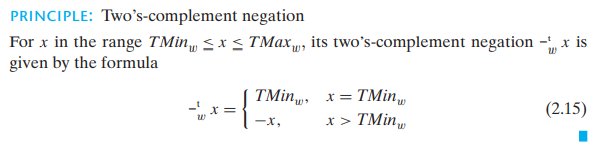

# 4.4 无符号数求反

w 位的 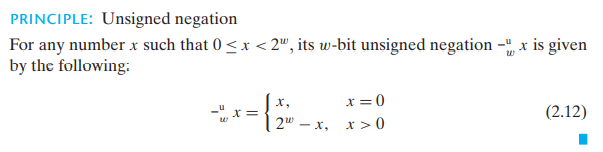其无符号逆元：

# 4.5 有符号数补码取非

w 位的 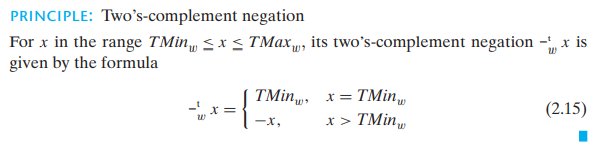其补码取非：

  • signed 和 unsigned 的非产生的位模式是相同的，都是各位取反再加1。

# 4.6 无符号数乘法

两个 w 位的 unsigned 相乘 --> 真实结果需要 位 --> 丢弃高 w 位，保留低 w 位

# 4.7 补码乘法

  • unsigned 和 signed 乘法具有位级等价性（完整的乘积位级可能不同，但截断后的位级相同）

# 4.8 乘以常数

编译器经常试着用移位和加法运算的组合来代替乘以常数的乘法

u << k 等价于 （无论 u 是 unsigned 还是 signed）。

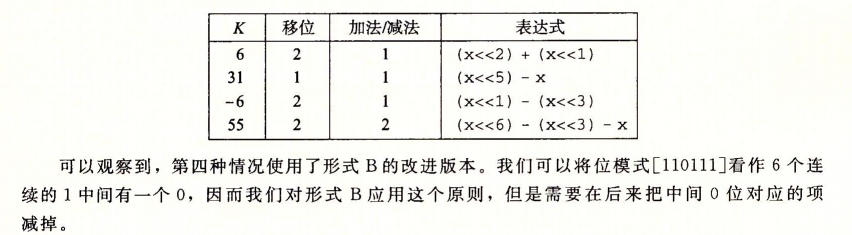
考虑一个任务，对于某个常数 K 的表达式 生成代码，编码器会将 K 的二进制表示表达为一组 0、1 交替序列：[(0...0)(1...1)(0...0)...(1...1)]，例如 14 可以写成[(0...0)(111)(0)]。考虑一组从位位置 n 到 m 的连续的 1（n >= m，对于14来说，n=3， m=1），我们可以用下面两种不同的形式来计算这些位对成绩的影响：

  • 形式 A：
  • 形式 B：

把这样连续的 1 的结果加起来，不用做任何乘法，我们就能计算出 。

Example

对于下面的每个 K，找出只用指定数量的运算表达 的方法：

# 4.9 除以 2 的幂

除以 2 的幂可以使用逻辑右移（unsigned）或者算术右移（signed）来达到目的。

# （1）无符号除法

产生

# （2）补码乘法

产生 （向下舍入）

问题：右移导致的是向下舍入，当我们希望向零舍入时，负数的右移会产生舍入方向的错误

解决：引入"偏置bias"来修正舍入： 产生 （向上舍入）

综上两种舍入方式，C 表达式 (x < 0 ? x + (1 << k) - 1 : x) >> k 会计算

提示

该表达式表示大于0时向下舍入，小于0时加上 bias 向上舍入

不幸的是，这种方法不能推广到除以任意常数。

# 4.10 代码安全问题

# （1）getpername 函数漏洞



 



int copy_from_kernel(void* dst, int maxLen) {
  int len = KSIZE < maxLen ? KSIZE : maxLen;
  memcpy(dst, kbuf, len);
  return len;
}
1
2
3
4
5

Bug：line4 将一个 int 传入了 size_t，若为 maxLen 传入负数会导致获取到内核额外的数据

# （2）XDR 安全漏洞


 




void copy_elements(void* src[], int cnt, size_t size) {
  void* ret = malloc(cnt * size);
  ... // 将 src 拷入 ret
  return;
}
1
2
3
4
5

Bug：此处乘法结果在赋值 size_t 类型时可能会产生溢出，导致少分配了空间

# （五）浮点数

# 5.1 二进制小数

小数点左移一位 <=> 被2除；右移一位 <=> 乘2

缺点：很多数无法精确表示

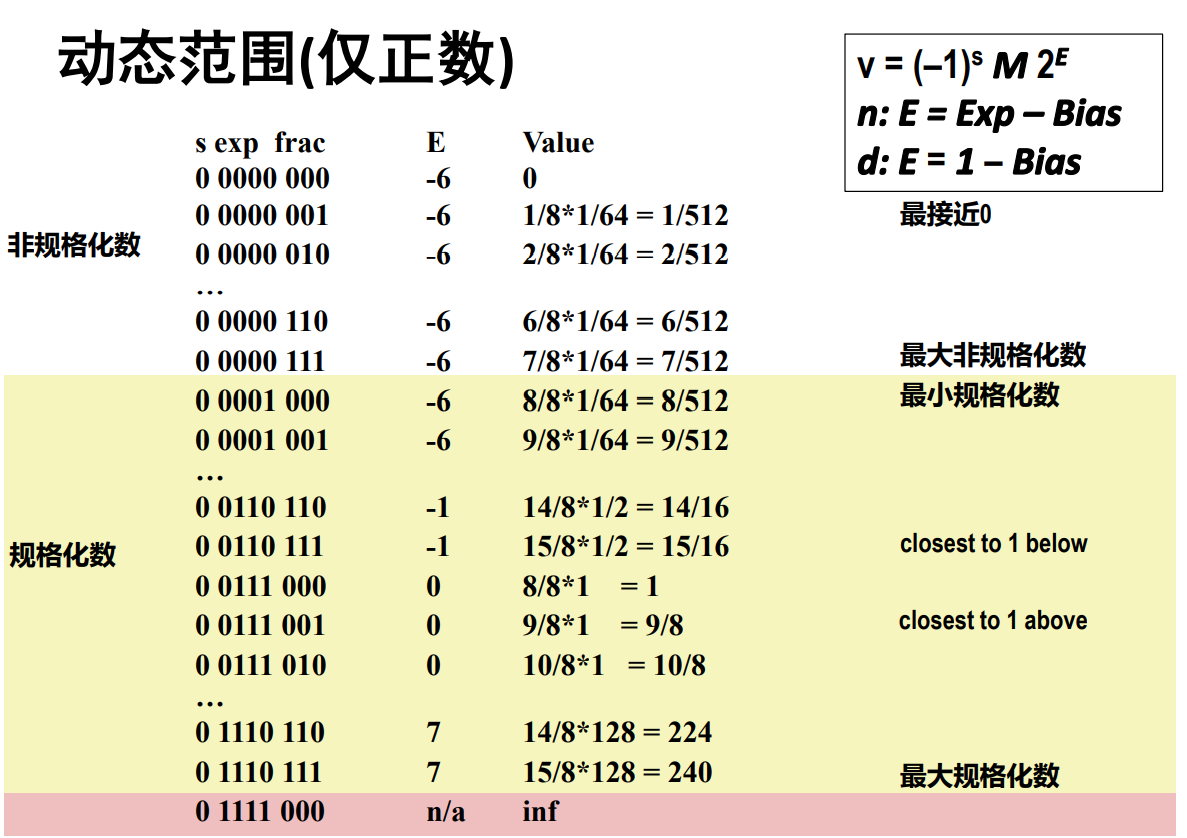
# 5.2 IEEE 浮点表示

  • 符号：正数 s=0，负数 s=1
  • 尾数：M 是一个二进制小数，范围：规格化时是 ，非规格化时是
  • 阶码：E 对浮点数加权，权重是 2 的 E 次方幂

浮点数的位被划分成三个部分：

  • 单独的符号位
  • k 位的阶码字段，编码为 E
  • n 位的小数字段，编码为 M

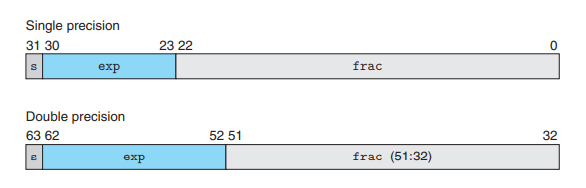
阶码的值决定了数的类型：

  1. 规格化的值：exp 位模式不全为0，也不全为1

    E = e - Bias, 其中

    M = 1 + f, 其中

    M = 1 + f 是因为有隐含的 1 开头

  2. 非规格化的值：exp 位模式全0

    E = 1 - Bias, M = f

    E 中的 "1-" 是为了平滑过渡用来补偿从中缺失的1，M 中没有隐含的 1.

  3. 特殊值：exp 位模式全1

  • ：frac 位模式全0时 s = 0时正无穷，s=-1时负无穷。可以用来表示溢出
  • ：frac 位模式非全0时 表示根号-1、无穷减无穷等

# 5.3 浮点数举例

它们并非均匀分布，而是越靠近原点则越稠密

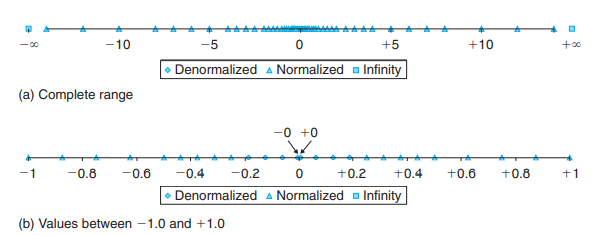
浮点数分布规律以及特殊值见 CSAPP P80，P82

当用8位表示浮点数时：

# 5.4 浮点数舍入

舍入模式：

  • 向0舍入
  • 向下舍入
  • 向上舍入
  • 向偶数舍入（default，“四舍六入五凑俩”）

向偶数舍入：试图找到一个最接近的匹配值，若原数是两个可能结果的中间数，则他将向上或向下舍入，使得结果最低有效数字是偶数

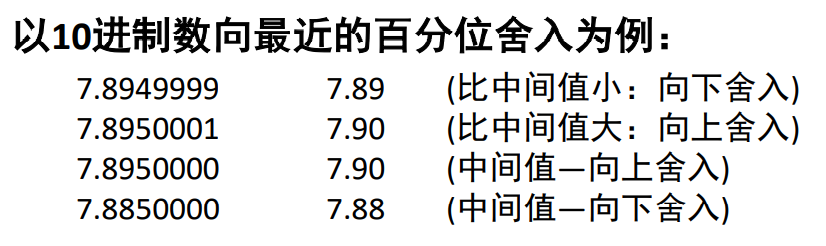
提示

“中间数”的呈现形式是所保留的位后面紧跟"1000...",即只有一个1，剩下全是0。

如10.010 -> 10.0; 10.110 -> 11.0

向偶数舍入可以避免很多统计误差

# 5.5 浮点运算

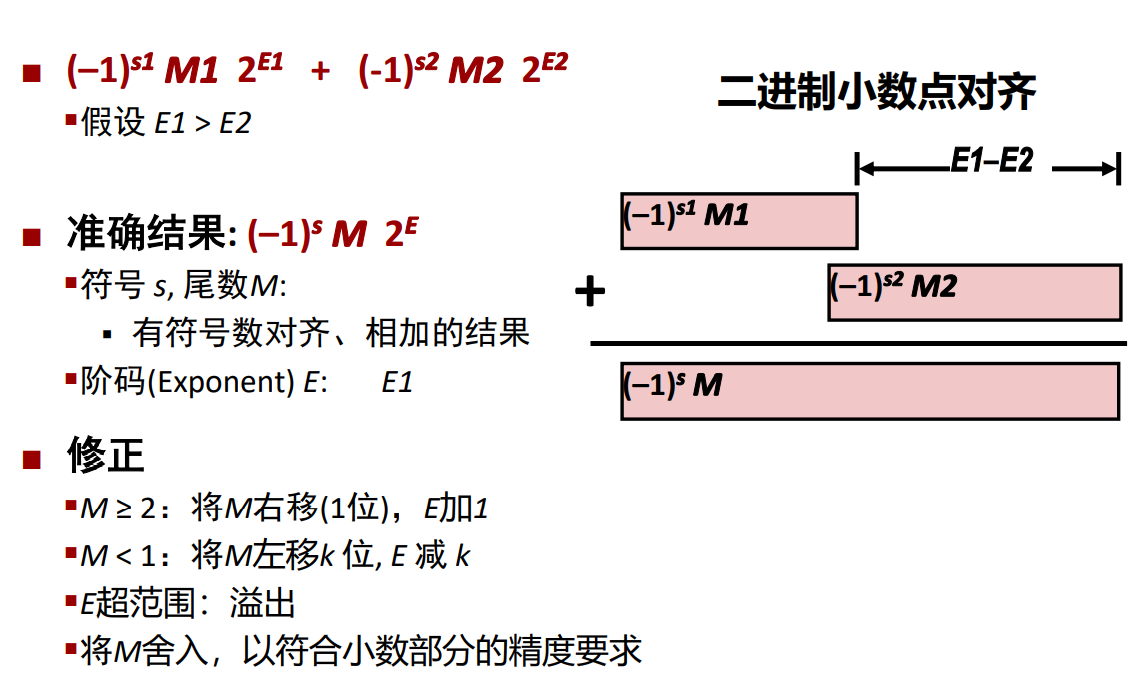
x + y = Round(x + y), 基本思想：

  • 首先，计算精确结果
  • 然后，变换到指定格式（E太大可能溢出，小数部分可能需要舍入）

计算精确结果 -> 修正（规格化）

# 浮点乘法

数学特性：

  • 不再满足结合性（因为不同的结合可能会产生不同的舍入）
  • 满足了单调性: 若 a >= b, 那对任何 a b x （除了NaN），都有 x + a >= x + b。

# 浮点数加法

数学特性：

  • 不再具有可结合性
  • 浮点乘法在加法上不具备分配性
  • 满足单调属性
  • 可保证只要 a != NaN, 就有 a * a >= 0.

# 5.6 C 语言的浮点数

在支持 IEEE 浮点格式的机器上，float、double 就对应于单精度和双精度浮点。 不幸的是，由于 C 语言标准不要求机器具有 IEEE 浮点，所有没有标准的方法来改变舍入方式或者得到 -0、、、NaN 之类的特殊值

int、float、double 之间的类型转换：
  • int -> float 不会溢出，但可能被舍入
  • float/double -> int 时，值会向 0 舍入，此时不再是位模式的重新解读
编辑 (opens new window)
#csapp
上次更新: 2021/12/07, 04:58:57
汇编基础

汇编基础→

最近更新
01
Deep Reinforcement Learning
10-03
02
误删数据后怎么办
04-06
03
MySQL 一主多从
03-22
更多文章>
Theme by Vdoing | Copyright © 2021-2024 yubincloud | MIT License
×