1. 二叉树的定义

1.1 相关概念

相关概念：父节点、子节点、兄弟节点、根节点、叶子节点

高度、深度、层：

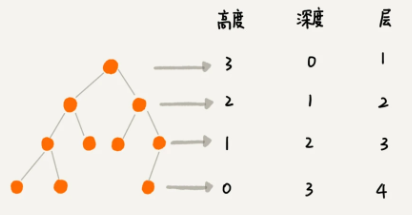
• 高度：就像我们说第几层楼时，说一楼、二楼是从最底下说的，这个高度也是。
• 深度：就像说海有多深一样，是从海平面开始算起的，这里也是，tree 是从根节点开始算起的。
• 层：跟深度的计算类似，不过，计数起点是 1，也就是说根节点位于第 1 层。

有一些特殊的二叉树：

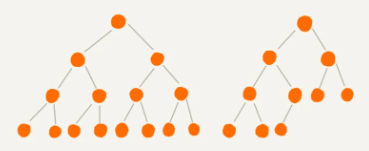
• 满二叉树：叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点（如下图左）
• 完全二叉树：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大（如下图右）

1.2 存储方式

两种存储方式：

1. 链式存储法

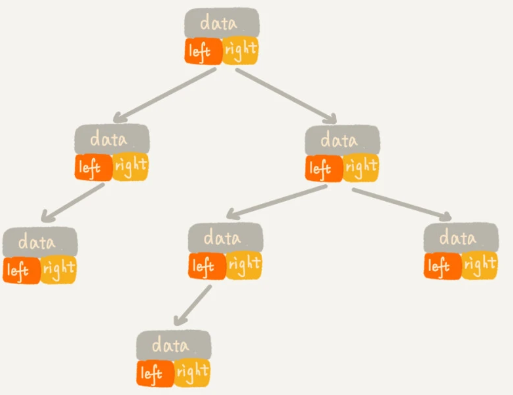
2. 顺序存储法

1.3 二叉树的遍历

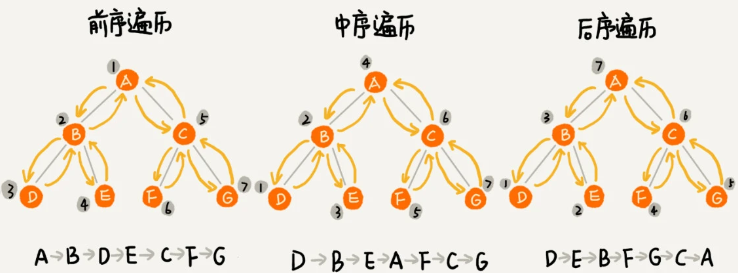
• 前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
• 中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
• 后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

相关代码：

void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印root节点
  preOrder(root->left);
  preOrder(root->right);
}

void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印root节点
  inOrder(root->right);
}

void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印root节点
}

从前、中、后序遍历的顺序图，可以看出来，每个节点最多会被访问两次，所以遍历操作的时间复杂度，跟节点的个数 n 成正比，也就是说二叉树遍历的时间复杂度是 O(n)。

2. 二叉查找树