1. 图的基本概念

2. 图的存储

3. 图的遍历

图的遍历是指从图中的某一顶点出发，按照某种搜索方法沿着图中的边对图中的所有顶点访问一次且仅访问一次。

3.1 广度优先搜索（BFS）

3.1.1 算法介绍

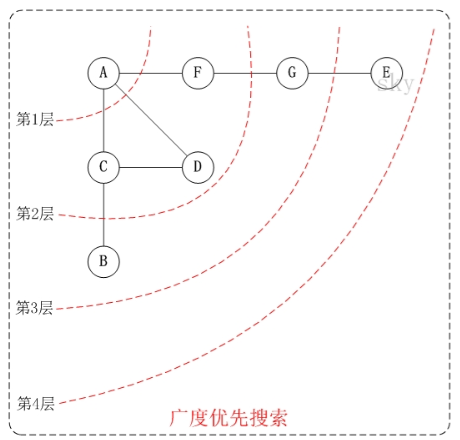
BFS 的核心思想应该不难理解的，就是把一些问题抽象成图，从一个点开始，向四周开始扩散。一般来说，我们写 BFS 算法都是用「队列」这种数据结构，每次将一个节点周围的所有节点加入队列。

广度优先搜索的伪代码（用邻接矩阵来实现）：

bool visited[MAX_VEXTEX_NUM];

void BFSTraverse(Graph G) {
    Queue Q;
    for (i = 0; i < G.vexNum; i++) {
        visited[i] = false;
    }
    for (i = 0; i < G.vexNum; i++) {
        if (!visited[i])
            BFS(G, i);
    }
}

void BFS(Graph G, int v) {
    visit(v);
    visited[v] = true;
    Q.offer(v);
    
    while (!Q.isEmpty()) {
        v = Q.poll();
        for (int x: v的所有邻居) {
            if (visited[x])
                continue;
            visit(x);
            visited[x] = true;
            Q.offer(x);
        }
    }
}

• 队列 Q 存储当前已经访问但还没有访问其邻居的节点，其中记忆的顶点要被用来访问其下一层顶点。
• visited 的主要作用是防止走回头路，大部分时候都是必须的，但是像一般的二叉树结构，没有子节点到父节点的指针，不会走回头路就不需要 visited。这里 visited 也可以用 Set 来实现。

3.1.2 BFS 性能分析

空间复杂度：需要借助队列 Q，n 个顶点均需要入队一次，在最坏的情况下，空间复杂度为 。

时间复杂度：

• 邻接表存储：每个顶点均需要搜索一次（入队一次），复杂度为 ，在搜索任一顶点的邻接点时，每条边至少访问一次，复杂度为 ，故算法总的时间复杂度为 。
• 邻接矩阵存储：查找每个顶点的邻接点所需的时间为 ，故算法总的时间复杂度为 。

3.1.3 BFS 求解单源最短路径问题

广度优先搜索总是按照距离由近到远来遍历图中每个顶点，因此 BFS 可以用来求非带权图中某一顶点到其余顶点的最短距离。

BFS 求解单源最短路径问题的算法如下：

void BFSMinDistance(Graph G, Node start) {
    Queue Q;
    // 初始化 d 和 path
    for (i = 0; i < G.vexNum; i++) {
        d[i] = ∞;  // d[i]表示从u到i的最短路径
        path[i] = -1;    // path[i]记录i在这个最短路径上的直接前驱
    }
    // 从 start 开始
    visited[start] = true;
    d[start] = 0;
    Q.offer(start);
    int step = 0;
    // 开始逐层对图进行遍历
    while (!Q.isEmpty()) {
        int sz = Q.size();
        for (i = 0; i < sz; i++) {  // 遍历当前这一层的所有节点
            Node cur = Q.poll();
            for (Node x: cur的所有邻居) {
                if (visited[x])
                    continue;
                visited[x] = true;
                d[x] = step;
                Q.offer(x);
            }
        }
        step++;  // 进入下一层，step+1
    }
}

3.1.4 广度优先生成树

...

3.2 深度优先搜索（DFS）

DFS 类似于树的先序遍历，尽可能“深”地搜索一个图。

递归实现

bool visited[MAX_VERTEX_NUM];

/**
 * 对图 G 进行深度优先遍历
**/
void DFSTraverse(Graph G) {
    for (int i = 0; i < G.vexNum; i++)
        visited[i] = false;
    for (int i = 0; i < G.vexNum; i++)
        if (!visited[i])
            DFS(G, i);
}

/**
 * 从顶点 v 出发，深度优先遍历 G
**/
void DFS(Graph G, int v) {
    visit(v);
    visited[v] = true;
    for (int x: v的所有邻居) {
        if (!visited[x]) {
            DFS(G, x);
        }
    }
}

• 图的邻接矩阵表示是唯一的，但对于邻接表来说，若输入的次序不同，生成的邻接表也不同，因此，对于同样一个图，基于邻接矩阵的遍历所得到的 DFS 序列和 BFS 序列是唯一的，基于邻接表的遍历所得到的 DFS 序列和 BFS 序列是不唯一的。

性能分析

空间复杂度：需要借助递归工作栈，故空间复杂度为 。

时间复杂度：

• 邻接表存储：查找所有顶点的邻接点所需的时间为 ，访问顶点所需的时间为 ，故算法总的时间复杂度为 。
• 邻接矩阵存储：查找每个顶点的邻接点所需的时间为 ，故算法总的时间复杂度为 。

最终的结论是与 BFS 一样的。

3.3 图的遍历与图的连通性

图的遍历算法可以用来判断图的连通性。

• 对于无向图，调用 BFS/DFS 函数的次数等于连通分量；
• 对于有向图，连通的有向图又分为强连通和非强连通，非强连通分量的一次调用 BFS/DFS 无法访问到该连通分量的所有节点。

4. 图的应用

4.1 最小生成树（最小支撑树）

连通图的生成树是包含图中所有节点的一个极小连通子图（n 个节点，n-1 条边）。

所有生成树中边的权值之和最小的是树是最小生成树。

最小生成树性质：

1. 不唯一；
2. 权值之和唯一；
3. ；
4. 最小生成树总是会采用联接每一割的最短跨越边。

用来得到最小生成树的算法有两个基于贪心策略的算法： Prim 算法和 Kruskal 算法，普加点，克连边。

Prim 算法

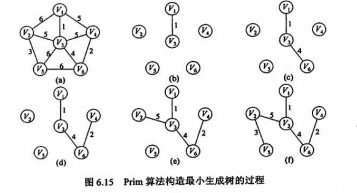
Kruskal 算法

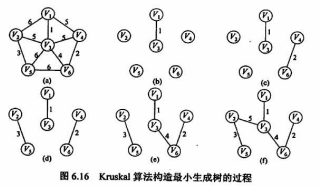
• Prim 算法的时间复杂度为 ，适合边稠密的图；
• Kruskal 算法的时间复杂度为 ，适合边稀疏而点较多的图。

4.2 最短路径算法

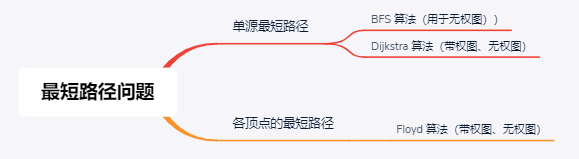
Dijkstra 算法

口语化表述：计算 u 到各顶点之间的最短距离，首先初始化 u 到自己的距离为 0，初始 dist[] 是图中本来的与 u 直观的距离（直接相连则为边的权值，不相连就是无穷）；然后从 dist[] 中选出距离最小的点加入结果集中，再计算其余的点到结果集的最短距离（通过比较原来到 u 的距离和经由新加入的点再到 u 的距离来判断是否更短了，如果更短的话就更新距离并记录该点的路径前驱是新加入的点），从中再选出距离最短的点加入结果集，之后重复上述过程直到所有点都加入了结果集。

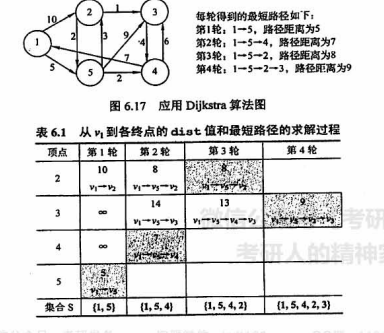
• Dijkstra 也基于贪心策略；
• Dijkstra 算法不适用带负权值的情况。

Floyd 算法

基本思想：通过递推产生一系列的 n 阶距离方阵 、、、，其中 表示从顶点 与 之间的最短路径和最短路径长度。

口语化表述：首先初始化 为图中直观的两两顶点距离（相连则为边的权值，不相连则为无穷），然后开始递推：先加入 作为中间节点，算一下两两节点之间若经由该中间节点是否更短，如果更短则更新，如果没有更短就不变，遍历完后得到 。不断如此直到获得 作为结果。

Floyd 核心代码（三 for 算法）：

// ... 先做初始化工作

for (int k = 0; k < n; k++) {  // 考虑以 v_k 作为中转点
    for (int i = 0; i < n; i++) {  // 两个 for 用 i、j 遍历整个矩阵
        for (int j = 0; j < n; j++) {
            if (A[i][j] > A[i][k] + A[k][j]) {  // 若以v_k为中转点的距离更短
                A[i][j] = A[i][k] + A[k][j];
                path[i][j] = k;  // 记录中转点
            }
         }
    }
}

4.3 拓扑排序（AOV 网）

AOV 网（Activity On Vertex），用顶点表示活动，有向边 表示活动 必须先于 。

拓扑排序：① 每个顶点只出现一次 ② 满足有向边定义的先后顺序。

提示

拓扑排序就是找到做事的先后顺序。

一个常用的拓扑排序算法：

1. 从 AOV 网中选一个没有前驱（入度为0）的节点并输出；
2. 从网中删除该节点和所有以它为起点的边；
3. 重复上述过程直至 AOV 网为空或当前网中不存在无前驱的节点，后一种情况说明该有向图存在环。

算法实现：

/**
 * 拓扑排序
 **/
bool topologicalSort(Graph G) {
    Stack S;  // 保存入度为 0 的点，用队列也可
    for (int i = 0; i < G.vexNum; i++) {
        if (indegree[i] == 0)
            S.push(i);   // 将所有入度为 0 的顶点入栈
    }
    int count = 0;       // 记录已输出的顶点个数
    while (!S.empty()) {
        int cur = S.pop();
        print(cur);  // 输出该顶点
        count++;
        for(int x: 以cur为起点的边所指向的所有顶点) {
            // 将所有 x 的入度 -1，若减为 0 则入栈
            indegree[x]--;
            if (indegree[x] == 0) {
                S.push(x);
            }
        }
    }//while
    return  true? count < G.vexNum: false;  // 指明是否排序成功，失败说明有环路
}

• indegree记录每个顶点的入度；
• stack保存入度为 0 的顶点（也可以用队列实现）

拓扑排序的注意点：

• 若存在一个顶点有多个直接后继，则拓扑排序结果通常不唯一；
• 邻接矩阵为三角阵的图，必存在拓扑序列。
• 复杂度：由于输出每个顶点时还要删除以它为起点的边，因此时间复杂度为：
  • 邻接表存储：
  • 邻接矩阵存储：

4.4 关键路径（AOE 网）

AOE 网（Activity On Edge），用边表示活动，顶点表示事件，边上的权值表示完成该活动的开销。

AOV网 vs. AOE网

相同点：都是有向无环图；

不同点：AOE 网的边有权值；AOV 网的边无权值，仅表示顶点之间的先后次序。

AOE 网的性质：

1. 只有在某顶点事件发生后，以它为起点的活动才能开始；
2. 只有当某顶点前面的所有活动都结束后，该顶点事件才能发生；
3. 活动可以并行进行。

AOE 网中仅有一个入度为0的点，称为源点（开始顶点）；仅有一个出度为0的点，称为汇点（结束顶点）。

从源点到汇点中，具有最大路径长度的路径称为关键路径，该路径上的活动称为关键活动。

完成工程的最短时间就是关键路径的长度，若关键活动不能按时完成，则整个工程将会延期。因此，只要找到了关键活动，就找到了关键路径，也就能够得出最短完成时间。

4.4.1 寻找关键活动时用到的几个参量

1. 事件 的最早发生时间 ：从源点 到顶点 的最长路径长度。该参量决定了从 开始的活动能够开工的最早时间。

ve 值的计算

• 源点；
• ，是的任意后继。

从前往后的顺序计算。程序实现时可以在拓扑排序的基础上计算：初始时所有节点的 ve = 0；每当输出一个入度为 0 的节点时，计算它所有直接后继节点的最早发生时间，若比之前更晚则更新（助记：前面还有别人，你得再等一会）。

2. 事件 的最迟发生时间 ：指在不推迟整个工程完成的前提下，即保证它的后继事件 在其最迟发生时间 能够发生时，该事件最迟必须发生的时间。

vl 值的计算

• 汇点汇点；// 该初始化保证了工程不延期
• ，是的任意前驱。

从后往前的顺序计算。程序实现时可以在逆拓扑排序的基础上计算：初始时所有节点的 vl = ve(汇点)；每当输出一个出度为 0 的节点时，计算其所有直接前驱的最迟发生时间，若比之前提早了则更新（助记：ddl提前了，再晚干活就延期了）。

3. 活动 的最早开始时间 ：指边所表示的活动的最早发生时间。若边表示活动，则有。

4. 活动 的最迟开始时间 ：指边所表示的活动的最晚开始时间，它的值等于终点事件的最迟发生时间与活动所需时间之差。若边表示活动，则有 。

5. 活动的最迟发生时间 和最早开始时间 的差额【摸鱼时间】 ：指在不使工程延期的情况下，活动可以拖延（摸鱼）的时间。若一个活动的时间余量为0，则说明该活动不得拖延，即为关键活动。

4.4.2 求关键路径的算法

算法步骤：

1. 求点最早开始时间 ve：从前往后求 ve，其中 ve(源) = 0；
2. 求点最晚开始时间 vl：从后往前求 vl，其中 vl(汇) = ve(汇)；
3. 求弧最早开始时间 e：e 等于弧起点的 ve；
4. 求弧最晚开始时间 l：l 等于弧终点的 vl 减去活动时间；
5. 不能摸鱼的是关键活动：l = e 的是关键活动。

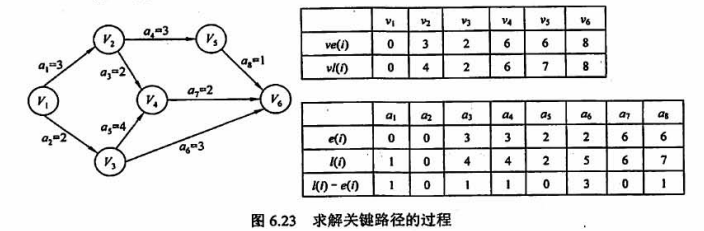
注意点：

• 关键路径上的活动是关键活动，可以缩短其时间来缩短工期，但不能无限缩短，到了一定的度，该活动就可能变成非关键活动了。
• 网的关键路径不唯一。只有加快那些包括在所有关键路径上的关键活动才能缩短工期。