动态规划基本技巧

# 1. 算法讲解

本部分参考自动态规划详解 (opens new window)

动态规划问题的一般形式就是求最值。动态规划其实是运筹学的一种最优化方法，只不过在计算机问题上应用比较多，比如求最长递增子序列呀，最小编辑距离等。求解动态规划的核心问题是穷举。因为想求最值，肯定要把所有可行的答案穷举出来，然后在其中找最值呗。

但既然核心问题是穷举，为什么会感觉到难呢？

首先，动态规划的穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。
而且，动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。
另外，虽然核心思想是穷举求最值，但是问题可以千变万化，穷举所有可行解并不是一件容易的事，只有列出正确的「状态转移方程」 才能正确地穷举。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。在实际的算法问题中，写出状态转移方程是最困难的，这里提供一个思维框架来作为辅助：

明确「状态」 -> 定义 dp 数组/函数的含义 -> 明确「选择」-> 明确 base case。

下面通过斐波那契数列问题和凑零钱问题来详解动态规划的基本原理。前者主要是让你明白什么是重叠子问题（斐波那契数列严格来说不是动态规划问题），后者主要集中于如何列出状态转移方程。只有简单的例子才能让你把精力充分集中在算法背后的通用思想和技巧上，而不会被那些隐晦的细节问题搞的莫名其妙。

# 示例 1：斐波那契数列

# （1）暴力递归

斐波那契数列写成代码是：

int fib(int N) {
    if (N==1 || N==2)
        return 1
    return fib(N-1) + fib(N-2);
}

1
2
3
4
5

这样写代码虽然简洁易懂，但是十分低效，低效在哪里？假设 n = 20，画出递归树如下：

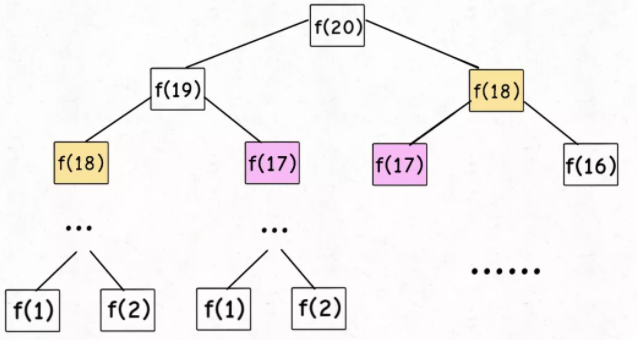
PS：但凡遇到需要递归的问题，最好都画出递归树，这对你分析算法的复杂度，寻找算法低效的原因都有巨大帮助。

从递归树中可以看出，想要计算原问题f(20)，我就得先计算出子问题f(19)和f(18)，然后要计算f(19)，我就要先算出子问题f(18)和f(17)，以此类推。最后遇到f(1)或者f(2)的时候，结果已知，就能直接返回结果，递归树不再向下生长了。

递归算法的时间复杂度怎么计算？子问题个数乘以解决一个子问题需要的时间。子问题个数，即递归树中节点的总数，而显然二叉树节点总数为指数级别，所以子问题个数为。解决一个子问题的时间，在本算法中，没有循环，只有 f(n-1) + f(n-2) 一个加法操作，时间为。所以时间复杂度为，指数级别，爆炸。

观察递归树，很明显发现了算法低效的原因：存在大量重复计算，比如f(18)被计算了两次，而且你可以看到，以f(18)为根的这个递归树体量巨大，多算一遍，会耗费巨大的时间。更何况，还不止f(18)这一个节点被重复计算，所以这个算法及其低效。

这就是动态规划问题的第一个性质：重叠子问题。下面，我们想办法解决这个问题。

# （2）带备忘录的递归解法

既然耗时的原因是重复计算，那么我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到备忘录里再返回；每次遇到一个子问题先去备忘录里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。可以使用数组或哈希表来充当这个备忘录。

int fib(int N) {
    if (N < 1) return 0;
    // 备忘录全初始化为 0
    vector<int> memo(N + 1, 0);
    // 初始化最简情况
    return helper(memo, N);
}

int helper(vector<int>& memo, int n) {
    // base case 
    if (n == 1 || n == 2) return 1;
    // 已经计算过
    if (memo[n] != 0) return memo[n];
    memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
    return memo[n];
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

现在画出递归树可以看到，借助备忘录，我们把一棵存在巨量冗余的递归树通过剪枝改造成了一幅不存在计算冗余的递归图，从而极大减少了子问题的个数。

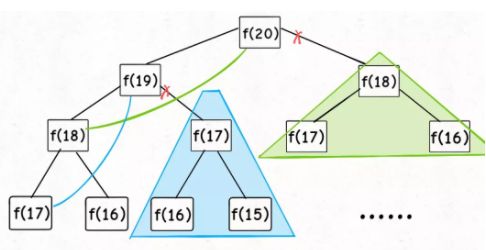
于是现在子问题只剩下了 f(1),f(2),f(3)…f(20)，数量和输入规模 n = 20 成正比，所以子问题个数是。解决子问题时没有循环，时间复杂度仍然是。所以本算法的时间复杂度是，比起暴力算法有了质的提升。

至此，带备忘录的递归解法的效率已经和迭代的动态规划一样了。实际上，这种解法和迭代的动态规划思想已经差不多，只不过这种方法叫做「自顶向下」，动态规划叫做「自底向上」。

什么叫自顶向下？注意我们刚才画的递归树（或者说图），是从上向下延伸，都是从一个规模较大的原问题比如说f(20)，向下逐渐分解规模，直到f(1)和f(2)触底，然后逐层返回答案，这就叫「自顶向下」。
什么叫自底向上？反过来，我们直接从最底下，最简单，问题规模最小的f(1)和f(2)开始往上推，直到推到我们想要的答案f(20)，这就是动态规划的思路，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。

# （3）dp 数组的迭代解法

有了上一步备忘录的启发，我们可以把这个备忘录独立出来成为一张表，就叫做 DP table 吧，在这张表上完成「自底向上」的推算岂不美哉！

int fib(int N) {
    vector<int> dp(N + 1, 0);
    dp[1] = dp[2] = 1;  // base case
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];
}

1
2
3
4
5
6
7

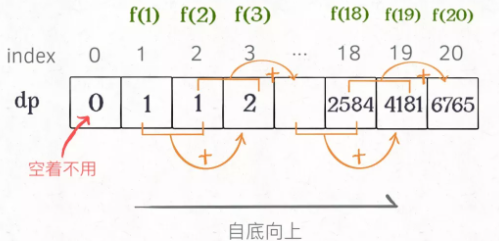
画出这个图就可以发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已。实际上，带备忘录的递归解法中的「备忘录」，最终完成后就是这个 DP table，所以说这两种解法其实是差不多的，大部分情况下，效率也基本相同。

这里引出 「状态转移方程」 这个名词，实际上就是描述问题结构的数学形式：

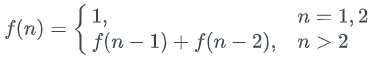
为啥叫「状态转移方程」？你把 f(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来，这就叫状态转移，仅此而已。你会发现，上面的几种解法中的所有操作，例如 return f(n - 1) + f(n - 2)，dp[i] = dp[i - 1] + dp[i - 2]，以及对备忘录或 DP table 的初始化操作，都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性，它是解决问题的核心。很容易发现，其实状态转移方程直接代表着暴力解法。所以千万不要看不起暴力解，动态规划问题最困难的就是写出状态转移方程，即这个暴力解。优化方法无非是用备忘录或者 DP table，再无奥妙可言。

这个例子的最后，讲一个细节优化。根据斐波那契数列的状态转移方程，当前状态只和之前的两个状态有关，所以并不需要那么长的一个 DP table 来存储所有的状态，只要想办法存储之前的两个状态就行了。因此可以进一步优化，把空间复杂度降为 O(1)：

int fib(int n) {
    if (n == 2 || n == 1) 
        return 1;
    int prev = 1, curr = 1;
    for (int i = 3; i <= n; i++) {
        int sum = prev + curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

1
2
3
4
5
6
7
8
9
10
11

斐波那契数列的例子并未涉及最优子结构，严格来说，这个例子不算动态规划，因为没有涉及求最值，以上旨在演示算法设计螺旋上升的过程。下面看第二个例子，凑零钱问题。

# 示例 2：凑零钱问题

题目：有 k 种面值的硬币，面值分别为，每种硬币的数量无限，再给一个总金额 amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。算法的函数签名如下：

// coins 中是可选硬币面值，amount 是目标金额
int coinChange(int[] coins, int amount);

1
2

比如说 k = 3，面值分别为 1，2，5，总金额 amount = 11。那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

你认为计算机应该如何解决这个问题？显然，就是把所有肯能的凑硬币方法都穷举出来，然后找找看最少需要多少枚硬币。

# （1）暴力递归

这个问题是动态规划问题，因为它具有「最优子结构」。要符合「最优子结构」，子问题间必须互相独立。

什么是相互独立？

什么叫相互独立？你肯定不想看数学证明，现在用一个直观的例子来讲解。

比如说，你的原问题是考出最高的总成绩，那么你的子问题就是要把语文考到最高，数学考到最高…… 为了每门课考到最高，你要把每门课相应的选择题分数拿到最高，填空题分数拿到最高…… 当然，最终就是你每门课都是满分，这就是最高的总成绩。得到了正确的结果：最高的总成绩就是总分。因为这个过程符合最优子结构，“每门科目考到最高”这些子问题是互相独立，互不干扰的。

但是，如果加一个条件：你的语文成绩和数学成绩会互相制约，此消彼长。这样的话，显然你能考到的最高总成绩就达不到总分了，按刚才那个思路就会得到错误的结果。因为子问题并不独立，语文数学成绩无法同时最优，所以最优子结构被破坏。

回到凑零钱问题，为什么说它符合最优子结构呢？比如你想求 amount = 11 时的最少硬币数（原问题），如果你知道凑出 amount = 10 的最少硬币数（子问题），你只需要把子问题的答案加 1（再选一枚面值为 1 的硬币）就是原问题的答案，因为硬币的数量是没有限制的，子问题之间没有相互制约，是互相独立的。

那么，既然知道了这是个动态规划问题，就要思考如何列出正确的状态转移方程：

先确定「状态」，也就是原问题和子问题中变化的变量。由于硬币数量无限，所以唯一的状态就是目标金额amount。
然后确定dp函数的定义：函数 dp(n) 表示当前的目标金额是n，至少需要dp(n)个硬币凑出该金额。

然后确定「选择」并择优，也就是对于每个状态，可以做出什么选择改变当前状态。具体到这个问题，无论当的目标金额是多少，选择就是从面额列表coins中选择一个硬币，然后目标金额就会减少：

# 伪码框架
def coinChange(coins: List[int], amount: int):
    # 定义：要凑出金额 n，至少要 dp(n) 个硬币
    def dp(n):
        # 做选择，需要硬币最少的那个结果就是答案
        for coin in coins:
            res = min(res, 1 + dp(n - coin))
        return res
    # 我们要求目标金额是 amount
    return dp(amount)

1
2
3
4
5
6
7
8
9
10

最后明确 base case，显然目标金额为 0 时，所需硬币数量为 0；当目标金额小于 0 时，无解，返回 -1：

def coinChange(coins: List[int], amount: int):

    def dp(n):
        # base case
        if n == 0: return 0
        if n < 0: return -1
        # 求最小值，所以初始化为正无穷
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            # 子问题无解，跳过
            if subproblem == -1: continue
            res = min(res, 1 + subproblem)

        return res if res != float('INF') else -1

    return dp(amount)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

至此，状态转移方程其实已经完成了，以上算法已经是暴力解法了，以上代码的数学形式就是状态转移方程：

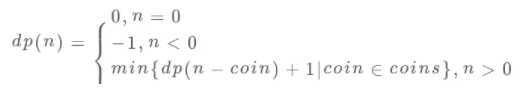
至此，这个问题其实就解决了，只不过需要消除一下重叠子问题，比如amount = 11, coins = {1,2,5}时画出递归树看看：

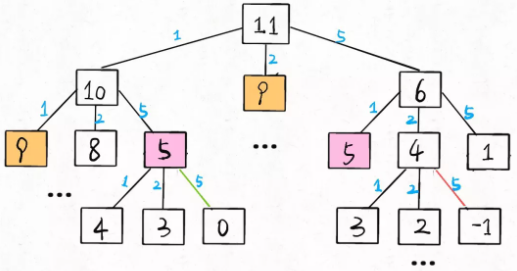
时间复杂度分析：子问题总数为递归树节点个数，这个比较难看出来，是，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为。所以总时间复杂度为，指数级别。

# （2）带备忘录的递归

只需要稍加修改，就可以通过备忘录消除子问题：

def coinChange(coins: List[int], amount: int):
    # 备忘录
    memo = dict()
    def dp(n):
        # 查备忘录，避免重复计算
        if n in memo: return memo[n]
        # base case
        if n == 0: return 0
        if n < 0: return -1
        # 求最小值，所以初始化为正无穷
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            if subproblem == -1: continue  # 子问题无解，跳过
            res = min(res, 1 + subproblem)

        # 记入备忘录
        memo[n] = res if res != float('INF') else -1
        return memo[n]

    return dp(amount)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

很显然「备忘录」大大减小了子问题数目，完全消除了子问题的冗余，所以子问题总数不会超过金额数 n，即子问题数目为 O(n)。处理一个子问题的时间不变，仍是 O(k)，所以总的时间复杂度是。

# （3）dp 数组的迭代解法 ⭐️

当然，我们也可以自底向上使用 dp table 来消除重叠子问题，dp数组的定义和刚才dp函数类似，定义也是一样的：dp[i] = x表示，当目标金额为i时，至少需要x枚硬币。

int coinChange(vector<int>& coins, int amount) {
    // 数组大小为 amount + 1，初始值也为 amount + 1
    vector<int> dp(amount + 1, amount + 1);
    // base case
    dp[0] = 0;
    for (int i = 0; i < dp.size(); i++) {
        // 内层 for 在求所有子问题 + 1 的最小值
        for (int coin : coins) {
            // 子问题无解，跳过
            if (i - coin < 0) continue;
            dp[i] = min(dp[i], 1 + dp[i - coin]);
        }
    }
    return (dp[amount] == amount + 1) ? -1 : dp[amount];
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

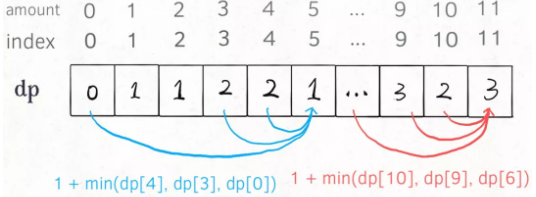
# 总结

第一个斐波那契数列的问题，解释了如何通过「备忘录」或者「dp table」的方法来优化递归树，并且明确了这两种方法本质上是一样的，只是自顶向下和自底向上的不同而已。

第二个凑零钱的问题，展示了如何流程化确定「状态转移方程」，只要通过状态转移方程写出暴力递归解，剩下的也就是优化递归树，消除重叠子问题而已。

计算机解决问题其实没有任何奇技淫巧，它唯一的解决办法就是穷举，穷举所有可能性。算法设计无非就是先思考“如何穷举”，然后再追求“如何聪明地穷举”。备忘录、DP table 就是在追求“如何聪明地穷举”。用空间换时间的思路，是降低时间复杂度的不二法门。

# 2. 动态规划的设计

本部分参考从最长递增子序列学会如何推状态转移方程 (opens new window)

我们借助经典的最长递增子序列问题（Longest Increasing Subsequence，LIS）来讲一讲设计动态规划的通用技巧：数学归纳思想，从而学会如何推出状态转移方程。

题目（来自 LeetCode 第 300 题）

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

注意子序列和子串的区别：子串一定是连续的，而子序列不一定是连续的。
示例：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4。

1
2
3

函数签名：

class Solution {
    public int lengthOfLIS(int[] nums) {
		...
    }
}

1
2
3
4
5

本题有动态规划解法和二分查找解法，这里只讲动态规划解法。

# 2.1 解法：动态规划

动态规划的核心设计思想是数学归纳法。在动态规划算法中有一个 dp 数组，我们可以假设 dp[0...i-1] 都已经被算出来了，然后问自己：怎么通过这些结果算出 dp[i]？这首先要定义清楚 dp 数组的含义，即 dp[i] 的值到底代表了什么。

这里我们的定义是：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。

PS：多做几道动态规划的题目后，会发现 dp 数组的定义方法也就那么几种。

根据这个定义，我们就可以推出 base case：dp[i] 初始值为 1，因为以 nums[i] 结尾的最长递增子序列起码要包含它自己。还可以得知最终结果（子序列的最大长度）就是 dp 数组中的最大值。

要思考如何设计算法逻辑进行状态转移，才能正确运行呢？这里就可以使用数学归纳的思想：假设我们已经知道了 dp[0..4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢？

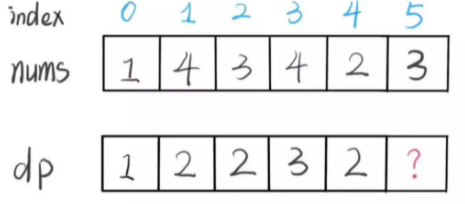
按照对 dp 的定义，现在想求 dp[5] 的值，也就是想求以 nums[5] 为结尾的最长递增子序列。nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成一个新的递增子序列，而且这个新的子序列长度加 1。显然，可能形成很多种新的子序列，但是我们只选择最长的那一个，把最长子序列的长度作为 dp[5] 的值即可：

for (int j = 0; j < i; j++) {
    if (nums[i] > nums[j]) 
        dp[i] = Math.max(dp[i], dp[j] + 1);
}

1
2
3
4

当 i = 5 时，这段代码的逻辑就可以算出 dp[5]。其实到这里，这道算法题我们就基本做完了。不过这只是算了 dp[5]，类似数学归纳法，其他的也都很容易计算了：

for (int i = 0; i < nums.length; i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) 
            dp[i] = Math.max(dp[i], dp[j] + 1);
    }
}

1
2
3
4
5
6

结合 base case，完整代码如下：

public int lengthOfLIS(int[] nums) {
    int[] dp = new int[nums.length];
    // base case：dp 数组全都初始化为 1
    Arrays.fill(dp, 1);
    for (int i = 0; i < nums.length; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) 
                dp[i] = Math.max(dp[i], dp[j] + 1);
        }
    }
	// 找出 dp 数组中的最大值
    int res = 0;
    for (int i = 0; i < dp.length; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

至此，这道题就解决了，时间复杂度为。

总结一下如何找到动态规划的状态转移关系：

明确 dp 数组所存数据的含义。这一步对于任何动态规划问题都很重要，如果不得当或者不够清晰，会阻碍之后的步骤。
根据 dp 数组的定义，运用数学归纳法的思想，假设 dp[0...i-1] 都已知，想办法求出 dp[i]，一旦这一步完成，整个题目基本就解决了。

但如果无法完成第二步，很可能就是 dp 数组的定义不够恰当，需要重新定义 dp 数组的含义；或者可能是 dp 数组存储的信息还不够，不足以推出下一步的答案，需要把 dp 数组扩大成二维数组甚至三维数组。

# 3. 最优子结构

到底什么才叫「最优子结构」，和动态规划什么关系？

「最优子结构」是某些问题的一种特定性质，很多问题其实都具有最优子结构，只是其中大部分不具有重叠子问题，所以我们不把它们归为动态规划系列问题而已。

比如这个场景：全校有 10 个班，已知每个班的最高分，求全校的最高分。这个问题就符合最优子结构，因为可以从每个班的最高分这个子问题算出全校最高分这个规模更大的问题的答案。

再比如这个场景：全校有 10 个班，已知每个班的最大分数差，求全校的最大分数差，这个问题就不符合最优子结构，因为无法从子问题中算更大规模的问题。那么遇到这种最优子结构失效情况，怎么办？策略是：改造问题。我们可以把这个问题等价转化：最大分数差，不就等价于最高分数和最低分数的差么，那不就是要求最高和最低分数么？于是便可以转化成具有最优子结构的问题并求其最值。

这两个例子旨在说明，最优子结构并不是动态规划独有的一种性质，能求最值的问题大部分都具有这个性质；但反过来，最优子结构性质作为动态规划问题的必要条件，一定是让你求最值的，以后碰到那种恶心人的最值题，思路往动态规划想就对了，这就是套路。动态规划不就是从最简单的 base case 往后推导吗，可以想象成一个链式反应，不断以小博大。但只有符合最优子结构的问题，才有发生这种链式反应的性质。

找最优子结构的过程，其实就是证明状态转移方程正确性的过程，方程符合最优子结构就可以写暴力解了，写出暴力解就可以看出有没有重叠子问题了，有则优化，无则 OK。这也是套路，经常刷题的朋友应该能体会。

# 4. dp 数组的遍历方向

二维的 dp 数组有正向遍历、反向遍历甚至是斜向遍历，如何选择呢？我们只要把住两点就行了：

遍历的过程中，所需的状态必须是已经计算出来的。
遍历的终点必须是存储结果的那个位置。

主要就是看 base case 和最终结果的存储位置，保证遍历过程中使用的数据都是计算完毕的就行，有时候确实存在多种方法可以得到正确答案，可根据个人口味自行选择。

编辑

上次更新: 2022/02/12, 16:11:00

← 图子序列类型问题→

动态规划基本技巧

# 1. 算法讲解

# 示例 1：斐波那契数列

# （1） 暴力递归

# （2）带备忘录的递归解法

# （3）dp 数组的迭代解法

# 示例 2：凑零钱问题

# （1）暴力递归

# （2）带备忘录的递归

# （3）dp 数组的迭代解法 ⭐️

# 总结

# 2. 动态规划的设计

# 2.1 解法：动态规划

# 3. 最优子结构

# 4. dp 数组的遍历方向

# （1）暴力递归