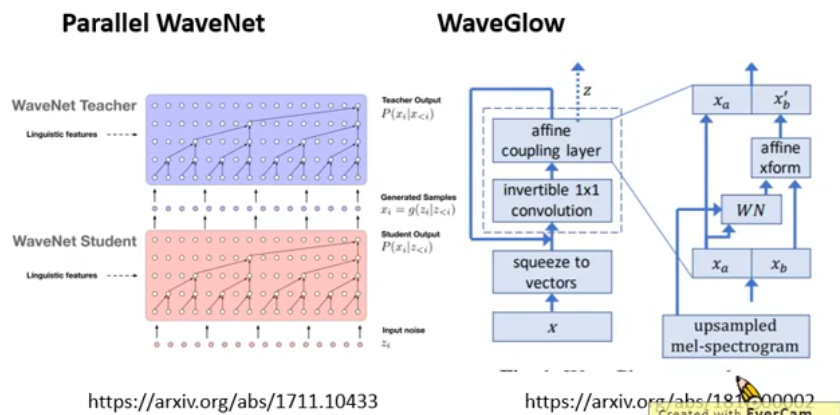
Flow-based Generative Model
Flow-based Generative Model
之前已经讲了三类 Generative Models:
- Component-by-component(Autoregressive model)
- 变分 Auto-Encoder
- GAN
但他们各自有各自的问题:
- Component-by-component(Autoregressive model)
- What is the best order for the components?
- Slow generation
- Variational Auto-encoder
- Optimizing a lower bound
- Generative Adversarial Network
- Unstable training
# 1. Generator
A generator G is a network. The network defines a probability distribution
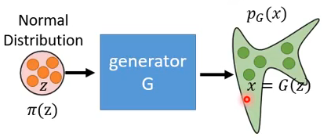
那对我们而言,什么样的 generator G 是我们想要找出来的呢?我们会希望 distribution
怎样让两者越接近越好呢?常见的做法是我们在训练 G 的时候,让他的训练目标是 maximize likelihood,也就是说我们从 distribution
为什么 maximize likelihood 就可以了呢?因为这个过程就等同于 minimize 两个 distribution 之间的 KL divergence:
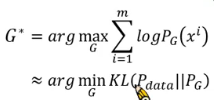
所以 maximize likelihood 就等同于让
而 Flow-based model 的好处就是:Flow-based model directly optimizes the objective function.(也就是可以直接 maximize likelihood)。
# 2. Math Background
要想理解 Flow-based model,你需要理解三样东西:Jacobian, Determinant, Change of Variable Theorem.
# 2.1 Jacobian Matrix
我们假设有如下的符号:
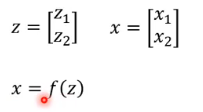
- z 和 x 都是多维 vector,而且两者的维度可以不一样,这里为了方便,举例的时候就假设都是 2 dim。
- 有一个 function f:x = f(z),你可以想象 f 就是你的 generator,z 就是你的 input,x 就是你 generate 出来的东西。
f 的 Jacobian 就是把 input component 和 output component 两两去做偏微分,然后全部收集起来得到一个 matrix:

如果写成
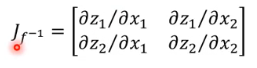
这两个 Jacobian 是有关系的,两个 matrix 的相乘等于 identity matrix。 所以说,如果函数就有 inverse 的关系,那他们的 Jacobian 也具有 inverse 的关系。
# 2.2 Determinant(行列式)
Determinant 就是给你一个 square matrix,有一个 operation,你把这个 matrix 代进去算一算,得到一个 scalar,这个 scalar 就是 determinant。
The determinant of a square matrix is a scalar that provides information aboput the matrix.
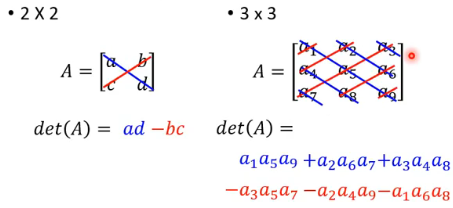
有几个结论要用:
一个 matrix 做 transpose 不会改变它的 determinant
determinant 有什么含义呢?determinant 指的是一个高维空间中“体积”的概念:
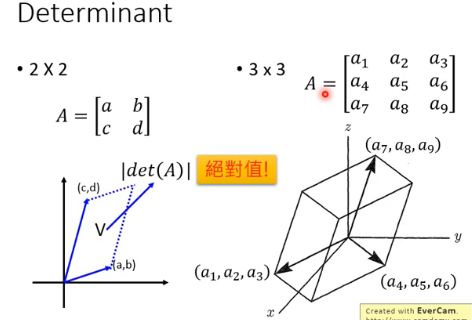
# 2.3 Change of Variable Theorem
我们有一个 distribution
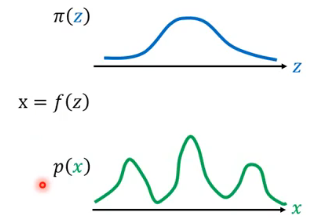
我们现在想知道
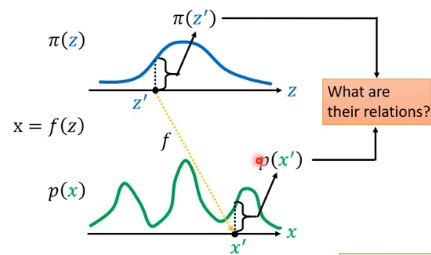
现在先举一个例子来说明我们问的问题到底是什么,下面是一个很简单的例子,其中
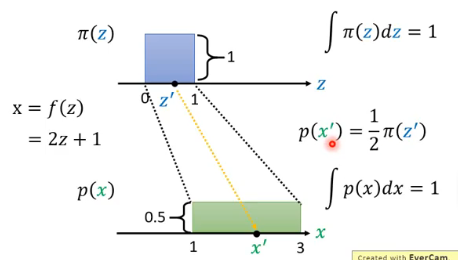
接下来考虑更加 general 的 case,我们不知道
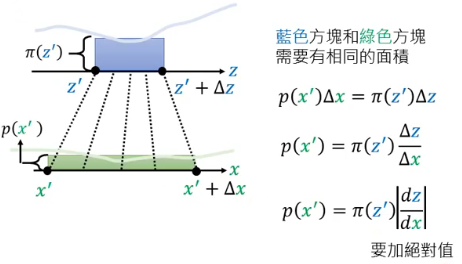
为什么要加绝对值呢?因为 z 和 x 的变化情况有下面两种可能:
刚刚的例子都是 z 和 x 是一维的,现在举一个 z 和 x 都是二维的情况:
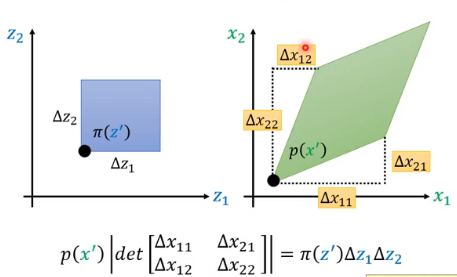
- 左边蓝色部分经过 f 变成了右边绿色部分
如果这一步没有问题的话,那接下来就只是对这个关系式进行一番整理就结束了:

- 可以得知,
- 重点是你要记住橙色标注的部分,这就是 Change of Variable Theorem。
# 3. Flow-based Model
之前我们要寻找的是
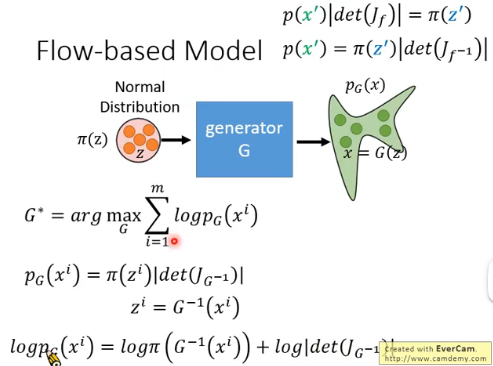
由上图可以看出,我们只需要 maximize
- 你需要能够计算
- 你需要能够知道
以上就是 G 的两个 limitation。
这个 G 是一个 network,正是由于 G 的 limitation,那一个 G 的能力可能有限,这时可以想到可以有多个 G,多个 G 连起来,能力可能就非常可观了,多个 G 就像一个 flow,所以称它为 flow-based model:
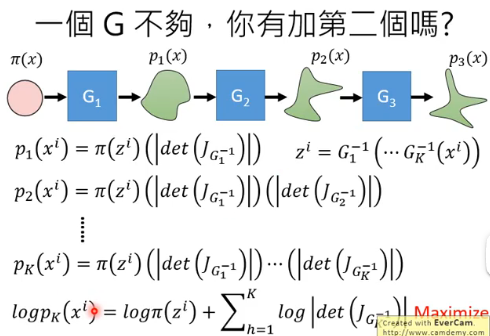
接下里就是 maximize 这个
那实际上,你是怎样 train 这个 Flow-based Model 的呢?我们先考虑只有一个 generator 的 case:
你会发现在
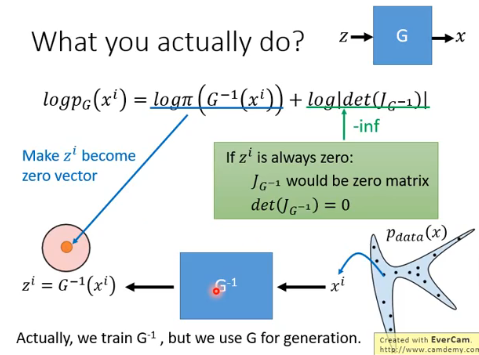
我们从真实的
但这会导致第二部分
# 4. Coupling Layer
# 4.1 Coupling Layer 是什么
一种 G 叫做 Coupling Layer,它的计算过程如下:
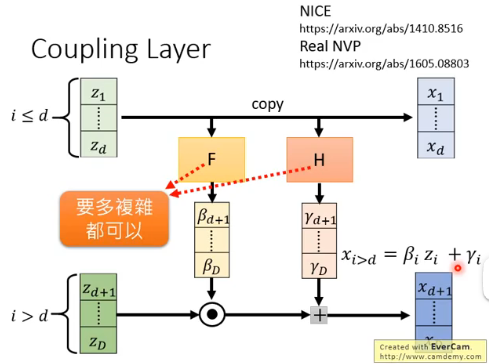
- z 被拆成了两个部分:1~d 和 d+1~D
- F 和 H 是一个任意的 network,要多复杂都可以
# 4.2 Couping Layer 的 inverse
现在就要来求 G 的 inverse:
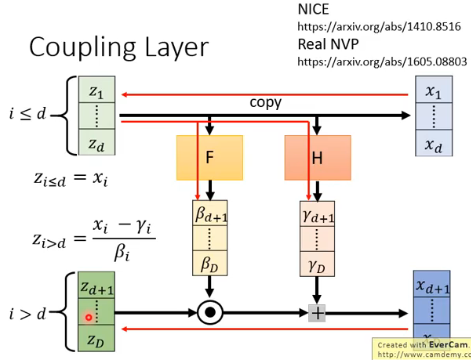
- 前 d 维只需要 copy 回去就好
- 后面这部分维度,因为
# 4.3 Coupling Layer 的 Jacobian
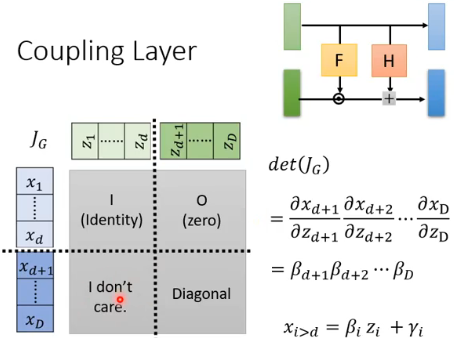
由于 x 和 z 都被分成了两部分,那 Jacobian
- 左上角部分:由于 x 是直接从 z copy 过去的,因此求微分就得到了 Identity;
- 右上角部分:由于 1~d 的 x 与 d+1~D 的 z 没有关系,因此这部分求微分得到 zero;
- 左下角部分:因为我们最终是想就 Jacobian 的 det,而右上角部分为 zero,所以这部分是啥已经无所谓了,所以 I don’t care.
- 右下角部分:根据 x 与 z 的关系:
对这个 Jacobian 求 det,可以看出结果就是右下角的 Diagonal 的 det,所以
# 4.4 Coupling Layer - Stacking
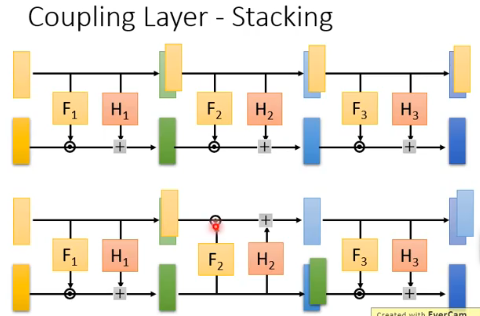
当我们把这种 Coupling Layer 叠起来,就得到了一个完整的 generator:
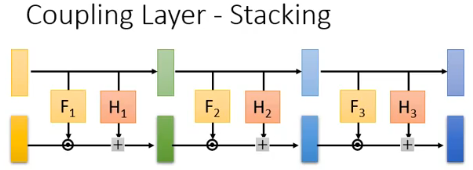
但当你把 Coupling Layer 叠起来的时候,会出现一个莫名其妙的问题。因为在 layer 的前后,vector 的前半段都是直接 copy 过去,那堆叠之后都是直接 copy,那最后上半段的 vector 就是什么都没有做。如果你今天用来 generate 一个 image,那么你会发现你 generate 的 image 的前半段都是输入进来的 Gaussian noise,这显然不是你期望的。
所以你在堆叠 Coupling Layer 的时候,需要做一点手脚,一种做法是在堆叠的时候故意让 copy 的位置产生交替:第一个 layer 是 copy 前半段,第二个 layer 是 copy 后半段…. 这样就避免了你把 Gaussian noise 带到最后 generate 的结果中,这个做法如下图的下面部分所示:
# 4.5 一个具体的例子
现在我们用一个 generate image 的具体例子来说一下是怎么做的。这时有两种做手脚的方法:
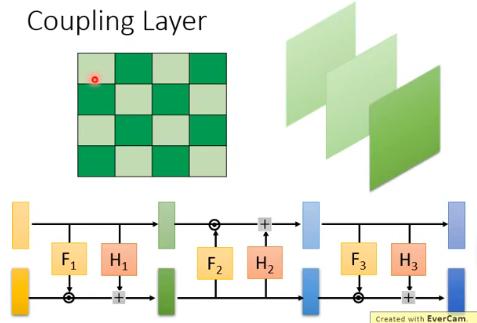
- 一种方法是,在一张 image 里面做手脚,一个 image 的 matrix 的每个元素有横纵坐标,那我们可以规定在第一个 layer 中,横纵坐标之和为奇数的做 copy,和为偶数的做 transform,然后在第二个 layer 中,横纵坐标之和为偶数的做 copy,和为奇数的做 transform。
- 另一种方法是,一个 image 可以分成 3 个 channel,那可以在第一个 layer 里面某个 channel 做 copy,另一部分 channel 做 transform。然后在第二个 layer 中再交替。
- 以上两种的 case 甚至可以交替使用。
# 5. GLOW
# 5.1 1 × 1 Convolution
1 × 1 Convolution 如下图所示,把第一个 pixel 的 3 个 value 组成的 vector,经过 3 * 3 的 W 得到输出的 3 个 value 组成的 vector,把它放到 output 的第一个 pixel 的位置:
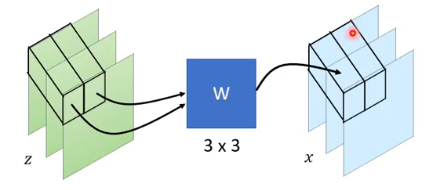
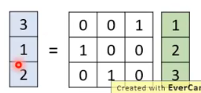
这个 W 是 learn 出来的,但这个 W 有什么含义呢?这个 W 有可能学会 shuffle the channels,比如:
If W is invertible, it is easy to compute
它的 Jacobian 呢?在一个 pixel 处:
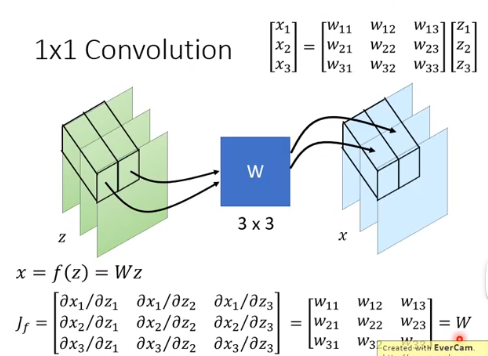
这一步很神奇。然后就可以得到:
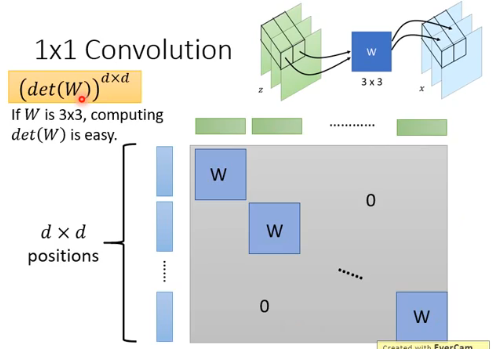
这个 d × d 的 Jacobian 中,横纵轴上的蓝绿色 vector 就是 image 中某个 position 的所有 channel 组成的 vector,不同 position 处没有关系,因此求微分是 zero,同一 position 的 pixel 处求微分就是 matrix
这个矩阵的 determinant 是很好算的,就等于
# 5.2 Demo
OpenAI 有一个关于 GLAW 的 demo:
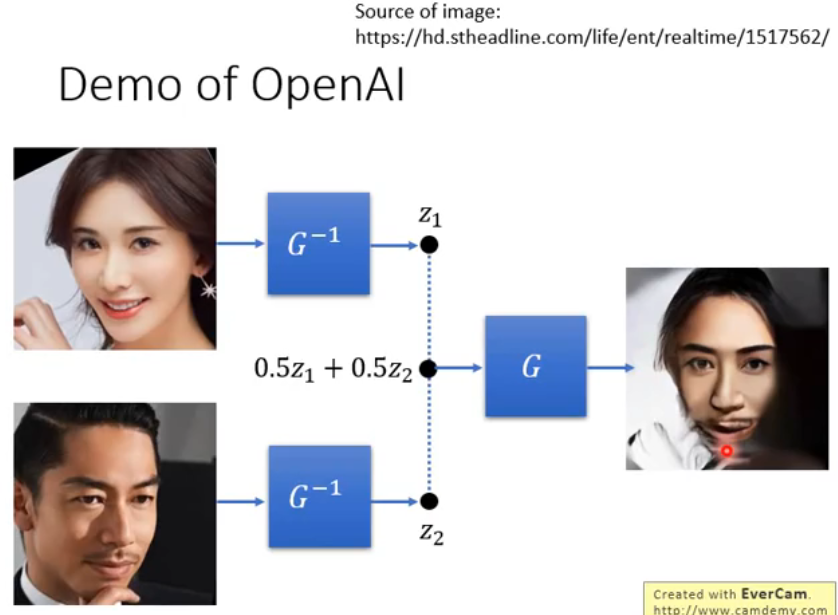
它还可以让人给笑起来。给他一堆 labeled 的笑与不笑的图片,它可以让人笑起来:
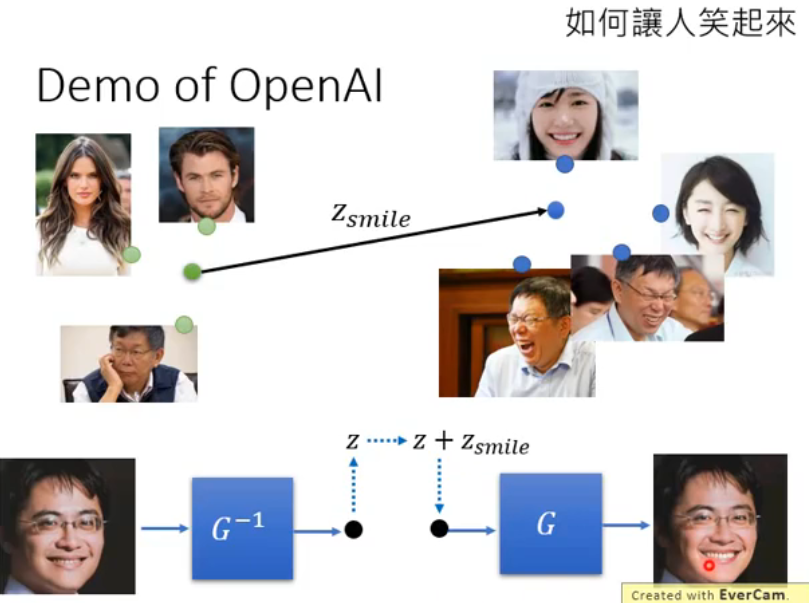
# 5.3 To Learn More …
GLOW 有很多应用,尤其是在语音合成上,因为不知道为什么,GAN 做语音合成的效果很差,下面是一些应用: