notebook
yubin
2022-04-10
目录

图神经网络

一篇发表在 distill 上的介绍 GNN 的博客也值得学习：A Gentle Introduction to Graph Neural Networks (opens new window)

# 1. Introduction

# 1.1 Graphs and where to find them

# 1）Images as graphs

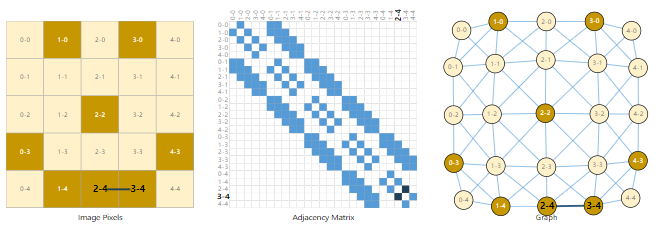
可以将 image 看成一个 graph，每一个 pixel 是一个 node，pixel 之间通过 edge 连接。这样每一个节点用 RGB 表示方式可以表示为一个 3 维 vector。

如果用一个 adjacency matrix 来表示 image 的话，一个 image 可以表示成一个 的 matrix。

image-20220410092941805

# 2）Text as graphs

可以将一段 text 视为一个 directed graph：

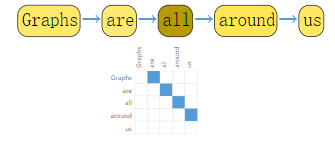
image-20220410093055576

当然 image 和 text 通常不会这样被编码，因为他们本身就有非常规整的结构，将其视为 graph 的话会产生冗余。

# 3）Graph-valued data in the wild

分子可以视为一个 graph，社交网络可以视为一个 graph，文章的引用也可以视为一个 graph …

# 1.2 What types of problems have graph structured data?

What tasks do we want to perform on graph data?

Level Goal Example
graph-level task predict the property of an entire graph 将分子视为一个 graph，预测其味道或者能否治疗某种疾病。也就是给整个 image 加一个 label。
node-level predicting the identity or role of each node within a graph 将一个社交网络中的人分成两个团体的人。比如一个武道馆，根据人与人之间的联系，将学生划分忠诚于两个老师的团体。
edge-level given nodes that represent the objects in the image, we wish to predict which of these nodes share an edge or what the value of that edge is. 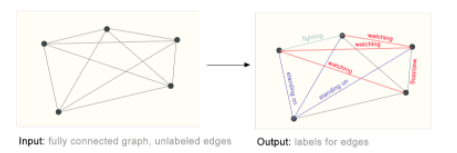image-20220410094602320

# 1.3 GNN: How?

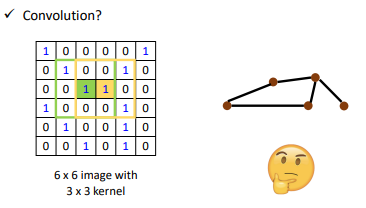
image-20220410094749334

How to embed node into a feature space using convolution?

  • Solution 1: Generalize the concept of convolution (corelation) to graph >> Spatial-based convolution
  • Solution 2: Back to the definition of convolution in signal processing >> Spectral-based convolution

# 1.4 Roadmap

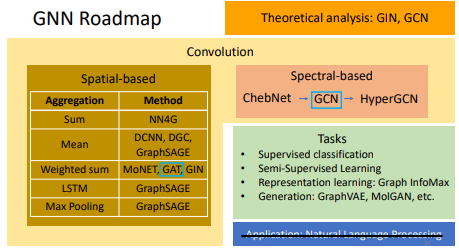
image-20220410094944372
  • 常用的还是 GAT 和 GCN 的 model
  • GNN 或许和 NLP 听上去像八竿子打不着的东西，但就是有办法把他们扯在一起

# 2. Spatial-based GNN

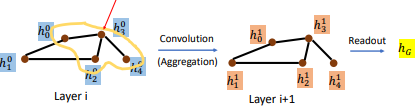
Terminology：

  • Aggregate：用 neighbor feature 来 update 下一个 hidden state
  • Readout：把所有 nodes 的 feature 集合起来代表整个 graph
image-20220410100744568
  • 比如用 、、 和 做一个 aggregate 便得到 。
  • 得到 之后就可以用来做整个 graph label 的 classification 或 prediction。

看一个人的偏好，通过观察与之有关系的人的偏好，可以从中进行预测，所以 aggregate 这种行为是比较符合实际的。

在 GNN 中，核心就是 ，不同的 就产生了不同的 GNN 架构。其中 H 是每一层的特征。

# 2.1 NN4G

NN4G（Neural Networks for Graph）

假设我们将一个分子视为一个图，原子是它的节点，将 graph 作为输入：

input layer：image-20220410101652634

此处每个 node 有一个 node feature，首先要经过一个 Embedding Layer 做一个 embedding，这里直接用一个 Embedding Matrix 来得到它的 feature：

image-20220410102221519

重点是接下来如何做 aggregation：

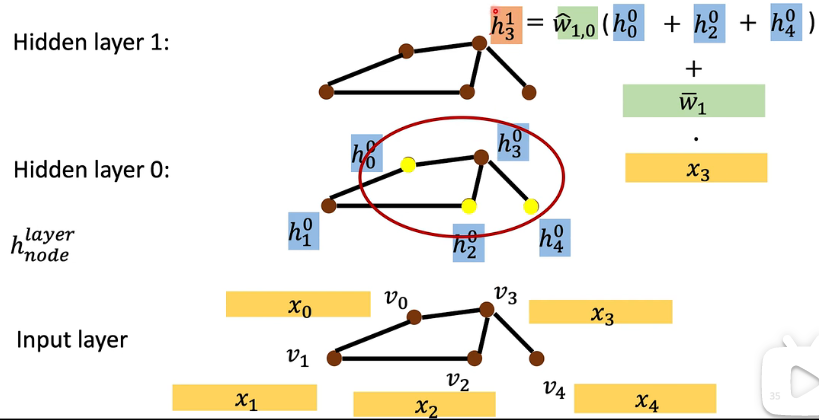
image-20220410102740576
  • 要计算 ，需要将上一层的 的邻居节点找出来做一个 sum，之后再加上原本的 input feature。具体计算过程可见上图。

将上述过程重复叠了多层之后（假如叠了 3 层），就要最后做一个 Readout：

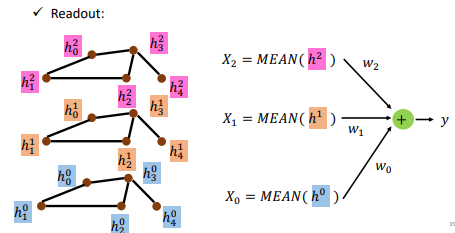
image-20220410103027587
  • 我们将每一个层的 node feature 各自全部加起来，然后经过一个 transform，再加起来变成一个 feature ，代表整个 graph 的 feature。

为什么用相加？其实也可以用其他方式，但多数用相加，可能是因为如果不相加的话会很难处理每个节点的邻居数量不同的这件事情。

# 2.2 DCNN

DCNN（Diffusion-Convolution Neural Network）

有了 input 之后，它做 update 的方式是这样子的：

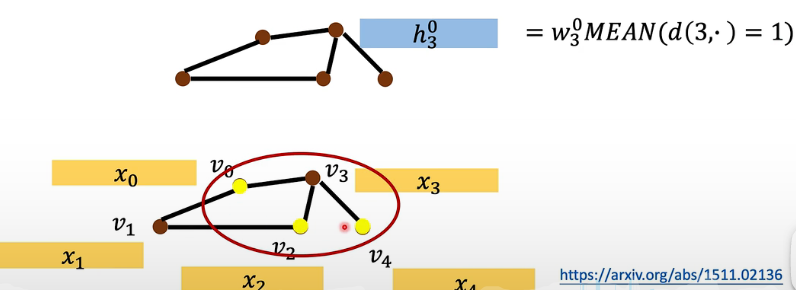
image-20220410103802957
  • 表示将与 3 这个节点距离为 1 的所有节点加起来再取个平均。
  • 取了平均之后再做一个 weight transform。其余的节点都做一样的事情。

再到第二层时与之前也有点区别：

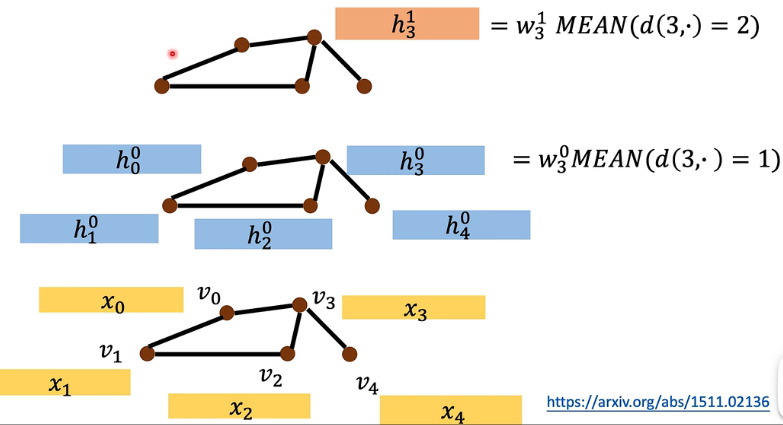
image-20220410104356790
  • 计算第 2 层的 hidden state 时，将与其距离为 2 的全部节点的 feature 都加起来再取平均，这里加的 feature 是 input layer 中的 input feature。
  • 这种情况下，假设我叠 k 层，那我就可以看到一个节点的 k neighborhood 里面得东西

最后计算一个节点的 feature 的方法是：

image-20220410104747709
  • 这样就可以得到 1 号这个节点的 output feature ，其余节点也类似。

# 2.3 DGC

DGC（Diffusion Graph Convolution），原论文 (opens new window)。它与上面的 DCNN 很像，就是在最后把所有 加在了一起：

image-20220410105429461

# 2.4 MoNET

MoNET（Mixture Model Networks），原文 (opens new window)。

之前做 aggregate 是把 neighbor feature 直接相加，但可能每个邻居的重要性不一样，所以这个网络就是用 weighted sum 替代了 simply summing up：

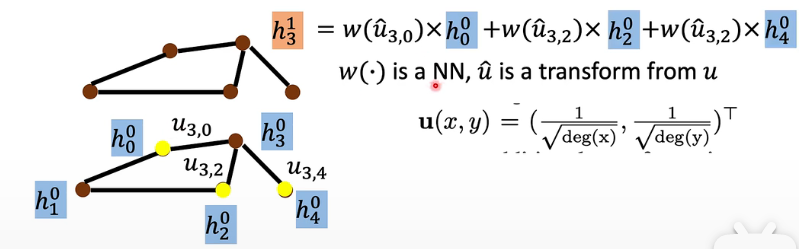
image-20220410110043556
  • 这里的 就代表了“距离”这一个概念，这里的距离是用 degree 定义的，但你也可以用其他方式来定义。

这里距离的定义是一开始就给出的，之后有的模型会让 model 自己学习这个距离的定义。

# 2.5 GraphSAGE

GraphSAGE， SAmple and aggreGatE。

它的 aggregation 方式：mean, max-pooling, or LSTM

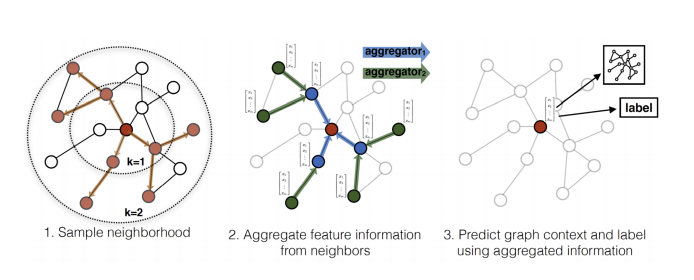
image-20220410110622938

有一种 aggregation 方式是 LSTM，它是把邻居的 feature 喂到 LSTM 中，然后把最后的 hidden state 当做他最后的一个 output，然后拿这个东西来做 update。但 LSTM 是 sequential 的，而邻居不应该有顺序啊，所以这里的做法是每次输入时都乱 sample 出一个顺序，每次 update 的时候都是 sample 出不同的顺序。所以最后可以学到说去忽略这个顺序的影响。

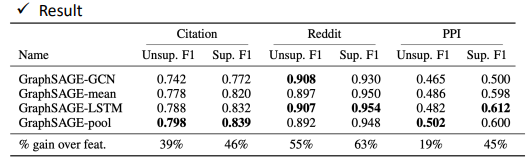
一个实验结果的对比：

image-20220410111026491

# 2.6 GAT

GAT，Graph Attention Networks，原论文 (opens new window)。

GAT 的重点是我不只做 weighted sum，这里的 weight 要让它自己去学，因此这样它做的方法就是我对邻居做 attention，方法是这样：

image-20220410111430197
  • 这里 得到的这个 energy 表示了对于 而言， 有多重要。其余的 energy 也是如此。

大家最喜欢用的 GNN 中，其中一个就是它。

# 2.7 GIN

GIN，Graph Isomorphism Network，原论文 (opens new window)。之前的 Network 我们是直接用，并没有关心它为什么会 work，但这个 GIN 直接告诉了我们有些方法会 work，但有些方法是不会 work 的，因此它还提供了一些理论证明，这里我们直接说结论。

结论告诉我们，在 update 的时候，我们最好使用下面这种方式来 update：

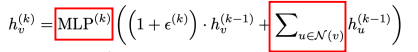
image-20220410122439413
  • 表示节点 v 在第 k 层的 hidden representation
  • 先把全部邻居的上一层的 先全部加起来，再加上 乘以自身上一层的 hidden representation。这里 可以自己学，但取 0 也是没问题的
  • MLP 是多层感知机，用 MLP 而不是 1 layer
  • 重点是用 部分应该用 sum 而不是 mean 或 max pooling

我们看一下 Sum instead of mean or max 的原因，先看一下的图：

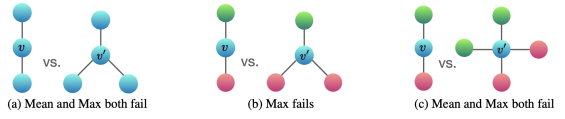
image-20220410123150332
  • 在 (a) 图中，如果采用 mean pooling，那么左右两个图得到的结果是一样的，此时无法区分这两个图是不同的图。另外的两个图类似。

# 3. Math of GCN ⚠️

参考 图卷积神经网络（GCN）的数学原理详解——谱图理论和傅立叶变换初探 (opens new window)

# 3.1 basic of GCN

Def：

  • ：adjacency matrix
  • ：degree matrix
  • ：单位阵
  • ：
  • ：

和 相当于给 A 和 D 加了一个自环，即单位阵。

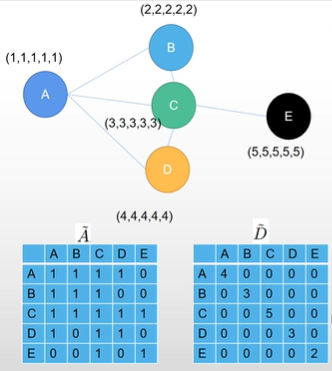
Example image-20220410160542342
  • 是对角线元素均为 1 的单位阵
  • 表示 i 号节点的 degree
  • 表示 i 和 j 节点之间有一条边

GNN 的核心公式：

GCN 的核心公式：

  • 由于 是一个对角阵，其 次方相当于对每个对角元素取 次方
  • 是一个可训练的参数，它对输入的 feature 做一个线性变换
  • 是一个非线性的激活函数

GCN 是处理 undirected simple graph 的

# 3.2 Spectral Graph Theory 谱图理论

谱图理论其实就是将线性代数研究矩阵的性质限定在了与图的邻接矩阵相关的一些矩阵上，所以它是线性代数的一个子领域。

# 3.2.1 线性代数相关知识复习

如果 且 为非零向量，那么说 是 A 的一个 eigen vector（特征向量）， 是 A 的一个 eigen value（特征值）。

实对称阵 A 一定有 n 个特征值，且对应着 n 个不相正交的特征向量。此时 A 可以分解成如下：

  • 为
  • 是正交阵，有

positive semi-definite matrix（半正定矩阵）指 n 个特征值都大于等于 0。

quadratic form（二次型）是说， 就是 对于矩阵 A 的二次型。

Rayleigh quotient（瑞丽熵）

这里可以证明，如果 是 A 的一个特征向量，那么其瑞丽熵就是对应的特征值。

# 3.2.2 常见的拉普拉斯矩阵

image-20220410173942405

这两个矩阵都是实对称阵，都有 n 个特征值和 n 个特征向量。他们都是半正定的。

这可以通过证明对于所有 ，其瑞丽熵都大于等于 0 即可。

进一步探索，可以证明一个更加严格的性质： 的特征值 range from [0,2]。

具体证明过程可参考视频。

# 3.3 fourier transformation 傅里叶变换

fourier transformation 只是同一个事物在不同域里面不同的视角而已，而对这个事物本身并没有发生什么改变。

做傅里叶变换就是为了计算上的可操作性，比如声波在不同的域上有不同的表现，此时我们有一段时域上的音频，而已知男生的声音在频率上低一些，女生则高一些，就可以将这段声音放在频域上，于是就可以将男声和女声分开，再将女声 mute 掉，就可以实现只有男声了。

Fourier for Graph：由于 image 在空间域上具有规则的拓扑结构，因此我们可以做一个特定形状的 kernel 作为卷积核，但是 graph 具有任意复杂的拓扑结构，每个点具有不同数量的 neighbor，所以我们无法在空间域给他一个特定形状的 kernel。借助 fourier 的想法，我们把它变换到另一个域里面，在这个域里面，卷积是一个很容易的操作，做完卷积后再通过一个 fourier 逆变换变回到空间域中：

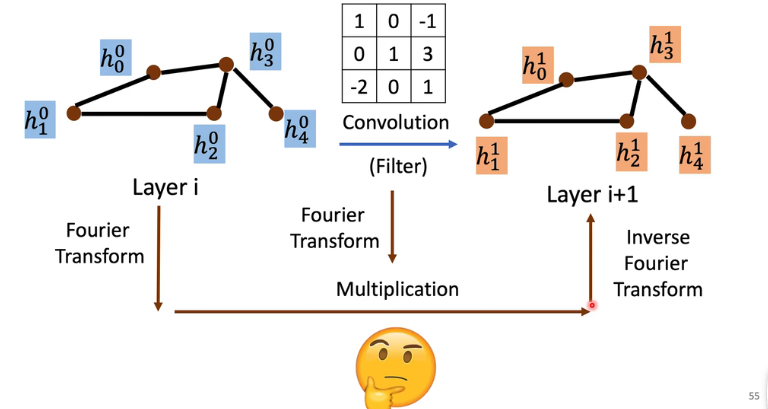
image-20220410172715982

如何在 graph 上做变换呢？我们来看一下 到底做了什么，这里拉普拉斯矩阵 在上一节讲过， 是 feature vector：

  • 运算结果是个 n × 1 的矩阵，观察这个结果，可以看出来，将 乘以 后，相当于对 feature 做了一个聚合邻居的操作。原来的 变成了 与它的邻居去做一些交互，这种邻居的聚合其实就是卷积的本质。这可以类比图像，图像的卷积就是与他的邻居做一个聚合。

而它与 fourier 变换有什么关系呢？由于 L 是实对称阵，所以可以写成：

  • 这一步，U 是正交阵，因此相当于 空间系基底的变换
  • 再乘 就是对每一个维度做一个放缩
  • 最后再乘 做一个逆变换，变回原来的基底

因此我们定义的在图上的 fourier 变换，就是乘一个 ，逆变换就是再乘一个 。在新的域中，我们对每个维度进行一个放缩操作，就起到了聚合邻居的效果。

这看起来很好，但在实际中求拉普拉斯矩阵 再做特征值分解是一个较为复杂的计算，在 graph 很大时会产生无法承受的开销。而 GCN 所做的就是对这种带特征值分解的傅里叶变换做了一些限制，从而推导出了一种不需要做特征值分解的、复杂度与边的数量呈线性关系的方法。

# 3.4 GCN 公式的推导

我们先要定义图上的卷积操作是什么样的。假定我们有一个函数 ，它的输入是图的邻接矩阵，而输出是图的性质比较好的矩阵，比如 或 ，这样的实对称阵性质是比较好的，这样我们可以设 分解为：，图上的卷积操作就可以定义为

  • 先经过一个 fourier 变换来换域，再在这个域里做一些操作，这个操作就是我们要学习的函数 。然后再变回原来的空间域。

可能你会看到这里还是有特征值分解，复杂度还没有降下来，因此我们可以对 做一个限制，限制它为 的多项式函数：

有了这个限制，便可以得到：

但实际操作中，我们的 不是用系数的形式去拟合多项式，因为随着 n 的变大，会有梯度消失或梯度爆炸的问题，实际情况中我们用的是切比雪夫多项式（递归定义）。其定义是：

之所以他不会发生梯度消失或梯度爆炸，是因为他有一个很好地性质，即 ，即不管 n 多大，它在数值上都会有一个稳定的摆动趋势，但缺点是对自变量有一个限制：其值位于 [-1,1] 之间。在这里也就是要求我们的 矩阵的特征值在 [-1, 1] 之间。之前我们证明过 的特征值在 [0,2] 之间，为了满足限制，只需要让 减去一个单位阵就可以了。所以我们最后使用的矩阵是：

F(A) 的结果是一个特征值位于 [-1,1] 的实对称阵，这样最后卷积的定义就可以写作：

化简后可以得到：

但这样需要计算矩阵的 k 次方，复杂度依然较高，所以我们做了一个近似，就只让 k 保留 0、1，2 阶以上就不再考虑了。所以可以得到：

而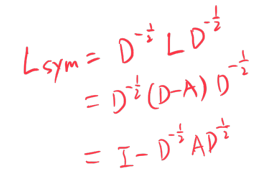：image-20220410194606444

所以就可以得到：。这已经很接近 GCN 的公式了。

再加一个 trick。为了让 与 共享参数，令 ，从而得到 ，这样 就没有必要存在了。

再加一个 renomolization 的 trick，将上面的 直接加到 里面去，从而得到 GCN 的公式：

这样就可以写出 GCN 核心公式：

加这些 trick 也只是因为这样做效果更好。

# 4. GCN 图卷积神经网络

PS：上面的数学推导要能看懂，但使用时候只需要知道下面这个过程就可以了。

GCN 核心公式：

但这个式子看起来也不太友善，可以被 rewritten 为：

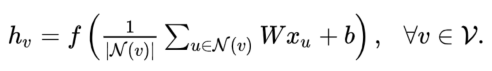
image-20220410200400327
  • 它表示，如果你要 update 某一个 v 的 feature map 的话，要做的事情就是把他所有的 neighbor（包括它自己）的 feature 经过一个 transform 后全部加起来，再加一个 bias，最后经过一个非线性激活函数后，就可以得到它在下一层的 feature representation。
GCN 解决了什么问题

GCN 之前的思想都是平均法：“你朋友的工资的平均值等于你的工资”。但是这有一些问题。

像下面这个社交网络，假如 B 是马云，A 是一个普通人，但他只认识马云，如果按照 GCN 之前的 network，他会把 B 的特征直接聚合过来，而这时不符合 A 的特征，毕竟 AB 之间差距比较大。而 GCN 就是解决了这个问题。

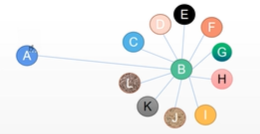
image-20220410200938599

看一下 GCN 公式的详细展开结果：

image-20220410201311620

只看最后一行，假如 i、j 表示 A、B，这时在更新 A 时会同时用到 A 和 B 的梯度，而 B 的社交关系比较多，不像 A 那么单一，因此 B 在发散自己的信息的时候会由于其 degree 较大而分摊开一部分，这样 B 聚合到 A 的信息较少了（因为公式最后一行的分母部分变大了），这样的话就避免了 B 把信息过多给了 A 而对 A 影响太大了。它解决的问题其实就是社交中有一些人，他们广交朋友，他认识到人多了，理所应当他分给每个人的信息也应当少一些，否则这对于整个社交网络的影响也太大了。GCN 其实就是在平均法的基础上对这个 “degree” 做了一个对称归一化。

# 5. Comparison between the above GNNs

# 5.1 Benchmark tasks

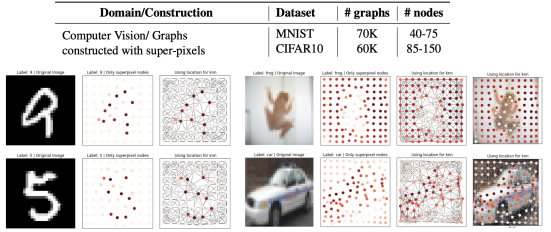
  1. Graph Classification: SuperPixel MNIST and CIFAR10
image-20220411142418056
  1. Regression: ZINC molecule graphs dataset
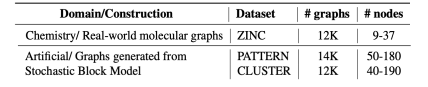
image-20220411142536011
  • 给一个 graph，透过这个分子来预测它的溶解度是多少
  1. Node classification:Stochastic Block Model dataset
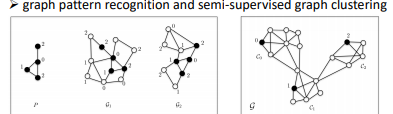
image-20220411142735332
  • 左图中，是说给一个 pattern ，然后要去 中，给出一个点，要识别它是否属于是 pattern 中的某一个点
  • 每一个 graph 有很多不同的 community 或 cluster，要做的事情就是去 identify 这些不同的 node 分别属于哪些 cluster
  1. Edge classification: Traveling Salesman Problem
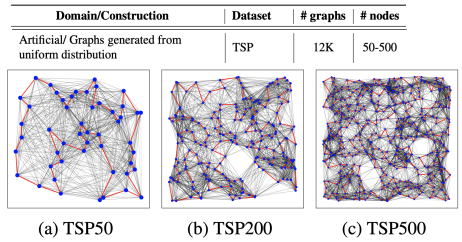
image-20220411144756299
  • 旅行商问题（Travel Salesman Problem，TSP），目标是 classify 某个 edge 是不是属于你的 TSP 最后的最佳路径的一个 edge

# 5.2 不同 model 的表现

# 1）SuperPixel

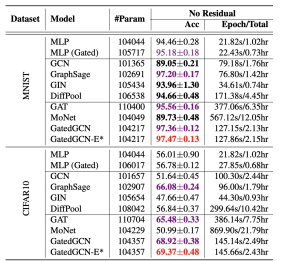
image-20220411145111669
  • 可以看到原生的 GCN 效果并不一定很好，因为 MLP 都可以打爆 GCN
  • 里面的 GatedGCN 是 GCN 的一个变种，可以把它理解成 GAT + GCN

# 2）Regression

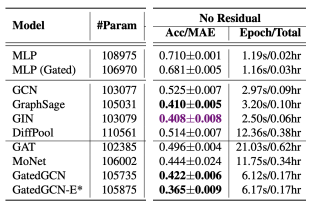
image-20220411145328862
  • 可以看到 GCN 是除了 MLP 里最惨的一个，GatedGCN 还是最强的

# 3）SBM

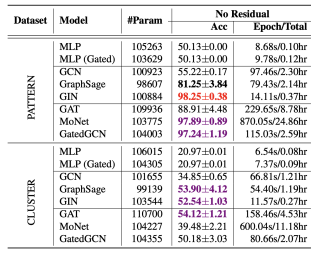
image-20220411145610949
  • GCN 还是很差的
  • 可以发现，有做 node weighted sum 的 model 大部分情况下比直接相加的好

# 4）TSP

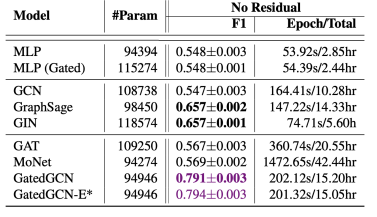
image-20220411145752921
  • 依然是 GCN 很惨，最好的是 GatedGCN
  • 这里的指标是 F1 score，就是 precision 和 report 加起来算的

我们再来看一下叠不同数量的 layer 有啥区别：

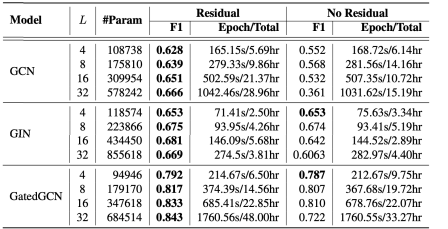
image-20220411152142837
  • 并不是说 layer 叠月多层越好，比如 No Residual 的 GCN。

当叠的层很多的时候，GCN 会出现 expressive power 或 exponentially decay，就是 node feature 经过很深的 GCN 之后，同样的 subgrade 里面很多东西会收敛到同样的地方。解决方法很简单：drop edge。

# 5.3 Drop Edge

之前 GCN update 时会对所有 neighbor 取平均，而 drop edge 是说在取平均的时候随便 drop 掉一些 neighbor，这样就可以避免刚刚的问题。但实际应用之后也只是提高了一些效果，仍然不是质的提高。

Summary

  • GAT 和 GCN 是我们常用的 GNN
  • 尽管 GCN 有一套完整的数学理论，但我们通常不会关系他们
  • GNN（or GCN）suffers from information lose while getting deeper。但目前还不清楚原因。
  • 很多人把其他 deep learning 的东西放到 graph 上做，出现了 GraphTransformer、GraphBert 等，但目前效果并没有说很好。
  • GNN can be applied to a varity of tasks.
编辑 (opens new window)
上次更新: 2022/10/03, 13:55:17
Pointer Network
Transformer

← Transformer→

最近更新
01
Deep Reinforcement Learning
10-03
02
误删数据后怎么办
04-06
03
MySQL 一主多从
03-22
更多文章>
Theme by Vdoing | Copyright © 2021-2024 yubincloud | MIT License
×