 神经网络压缩
神经网络压缩
为什么需要 smaller model 呢?因为有时候我们需要把 ML model 部署到 resource-constrained 的环境下,如智能手表、无人机等 loT device、edge device 上。为什么不在云端运算呢?这可能涉及到 lower latency、privacy 等理由。
我们这章只将在 soft-ware 上的 solution,而不涉及 hard-ware 上的 solution。
# 1. Network Pruning
# 1.1 What is Network Pruning
“树大必有枯枝”。Networks are typically over-parameterized (there is significant redundant weights or neurons),所以往往可以 prune them。
Network Pruning 是怎样进行的呢?大概如下图所示:
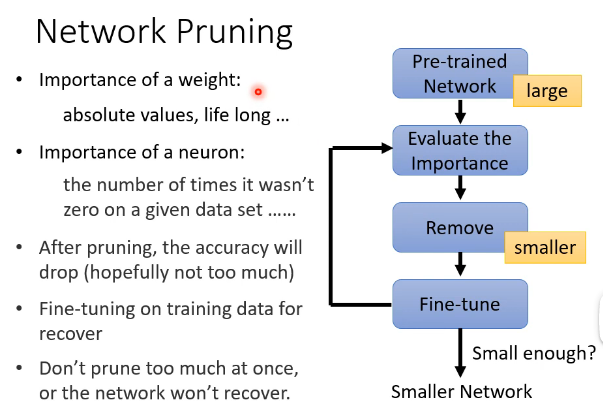
- 先 pretrain 一个很大的 model,然后评估里面 weight / neuron 的重要性,将一些不重要的 remove 掉,这样 accuracy 会掉一点,这时再 fine-tune 一下使 network 得到恢复,然后继续循环这个过程。
prune 的单位可以以 weight parameter 为单位,也可以以 neuron 为单位,那以这两者当作单位在实践中有什么不同呢?
# 1.2 Practical Issue
# 1.2.1 Weight pruning
假如我们是评估某一个 parameter 重不重要而决定能不能去掉,那我们把不重要的 parameter 去掉之后,得到的 Network 的形状可能会是不规则的:
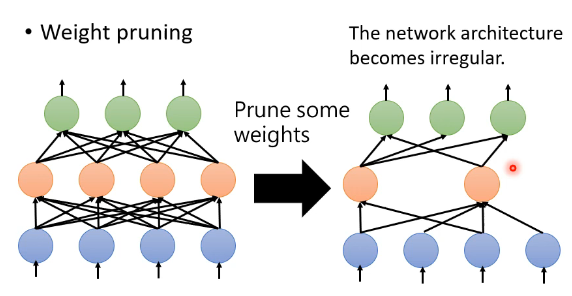
这种不规则带来的结果就是难以去实现,同时也不容易用矩阵的乘法、用 GPU 去 speed-up。
一篇 paper 探讨了 weight pruning 的效果:
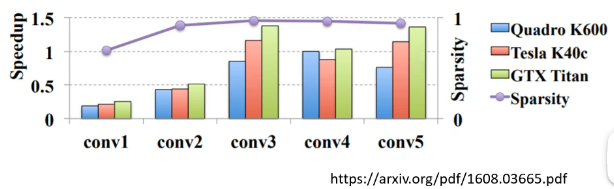
- 紫色的线对应“Sparsity”,后面接近 1 表示接近 95% 的 parameter 都被 prune 掉了,同时 accuracy 没有掉太多,但看 speed 的话,不同颜色的矩形表示在不同的 device 上运行,speed-up 大于 1 才会有加速,可以看到大部分的都是并没有起到加速的效果,反而还变慢了
说明把很多 parameter 给 prune 掉,使得 Network 变得不规则,反而使得在 GPU 资源上并没有起到期望的加速效果。因此,weight pruning 不见得是一个好的方法。
# 1.2.2 Neuron pruning
Neuron pruning 相对来说就是一个好一点的方法了:
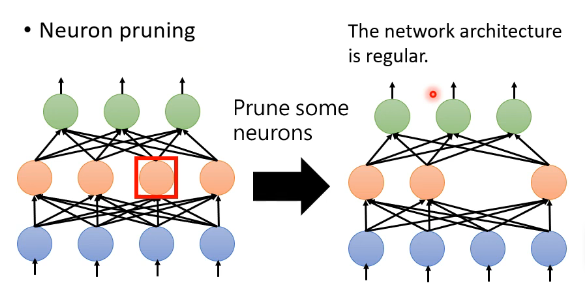
它比较容易用 pytorch 来实现,也比较好用 GPU 来加速。
# 1.3 Why Pruning - Lottery Ticket Hypothesis
# 1.3.1 Lottery Ticket Hypothesis
为什么是先 train 一个 large model 再让他变小,而不是直接 train 一个 smaller model 呢?
一个普遍的答案是大的 network 比较好 train。你会发现,你直接 train 一个小的 network 往往没有办法得到跟大的 network 做 pruning 完后的一样的正确率。
为什么 larger network 比较好 train 可以参考以前的李老师的录影。
还有一个解释是大乐透假说(Lottery Ticket Hypothesis)。我们知道 train 一个 network 是比较看人品的,抽到一组比较好的初始参数,结果可能就会比较好。那我们可以把 large network 视为多个小的 sub-network,train 一个 large network 就可以视为 train 多个 sub-network,每一个小的 sub-network 不一定能够成功被训练出来,但在众多的 sub-network 里面,只要其中一个人成功,就可以“一人得道,鸡犬升天”,这就好像玩大乐透的时候买很多彩票就会中奖率变高一样:
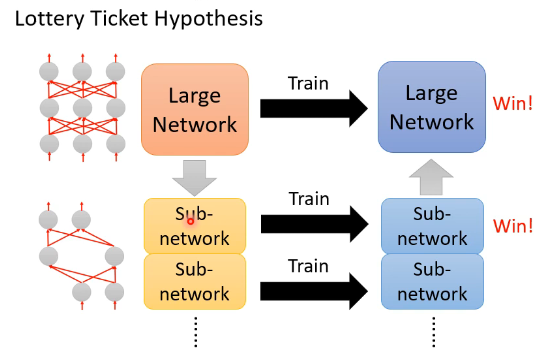
这个 Lottery Ticket Hypothesis 是怎样在实验中被证实的呢?如下图所示:
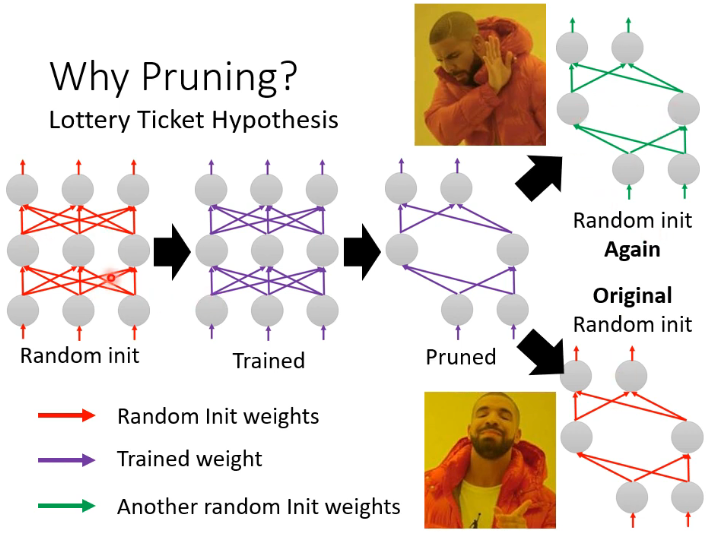
- 我们先 random init 一个 large network,然后 train 好后再进行 pruning 得到一个 small network。这时如果把这个 small network 重新 random init 一遍,会发现 train 不起来,但如果这个 small network 的参数与原始 large network 的初始参数相同,就可以 train 起来了。
# 1.3.2 Deconstructing Lottery Tickets
Lottery Ticket Hypothesis 是一个很著名的 hypothesis,后来有一篇 paper 是 Deconstructing Lottery Tickets: Zeros, Signs, and the Supermask (opens new window) 得出了很多有趣的结论,这里只讲它的结论。
# 1)Different pruning strategy
他做了很多实验尝试了不同的 pruning strategy,发现了某两个 strategy 是最有效的:
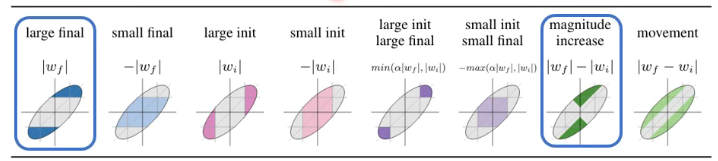
- 他发现训练前和训练后的绝对值差异越大,那 prune 掉那些 network 后得到的结果是越有效的。
# 2)“sign-ificance” of initial weights: Keeping the sign is critical
一组好的 initial weights 到底好在哪里呢? 研究发现说,如果 prune 完后的 small model 重新初始化时只要不改变原初始参数的正负号,就可以 train 起来。

这个实验说明,初始参数的正负号是这个 model 能不能 train 起来的一个关键因素。
# 3)Pruning weights from a network with random weights
就好像米开朗琪罗雕刻出大卫的过程被自己说是“不过是从一个大的石头里把大卫释放出来”一样,有没有可能从一个随机初始化的 large network 里面的一个小子集组成的 network 在不需要 train 时就已经可以做分类等任务了呢?实验发现答案是“是”,而且这样得到的效果还不错。
# 1.3.3 Rethinking the Value of Network Pruning
Lottery Ticket Hypothesis 就一定是对的嘛?不一定,有一篇 paper (opens new window) 做了一些实验打脸了 Lottery Ticket Hypothesis:
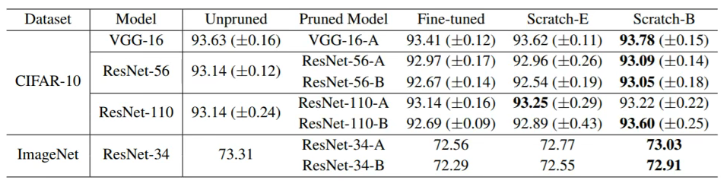
有一些 model,然后列出了 unpruned 的情况下的 performance,然后对 model 进行 prune 得到 small model,再进行 fine-tune,会发现 performance 与 unpruned 的差不多;然后 scratch-E 指的是真的重新对 small model 进行随机初始化参数(不是 original random init,即不是从原来 large model 的 init weights 中借过来的),这些 scratch-E 的 model 的 performance 果然如人们预期般不如原来 unpruned 的效果好,但是,实验发现再多 train 几个 epoch,结果就是 scratch-B 这一列,可以看到 performance 就达到了与原来的同一水平了。所以说,也许“小的 network 不如大的好 train”只是一个幻觉,只不过需要多 train 几个 epoch。
同时 paper 还指出,Lottery Ticket Hypothesis 是在某些情况下才能观察到,它只在 small learning rate、unstructured(指以 weight 作为单位来 pruning)的情况下才能观察到 Lottery Ticket Hypothesis 现象。
所以,Lottery Ticket Hypothesis 是真是假,还有待未来的研究来证实。
# 2. Knowledge Distillation
# 2.1 Knowledge Distillation 的基本概念
其实 Knowledge Distillation 的精神与 Network Pruning 有一些类似的地方。
Knowledge Distillation 的概念是这样,先 train 一个大的 network,叫做 Teacher Network,你要 train 的、真正想要的那个小的 network 叫做 Student Network。在 Knowledge Distillation 里面,student network 是要根据 teacher network 来学习得到。
student 怎么从 teacher 那里学习呢?以手写数字分类为例:

- 先把训练资料全丢给 teacher,然后 teacher 产生 output,这里是 output 一个 distribution。接下来,给 student 一模一样的 input,但是 student 不是看正确答案来学习,而是看 teacher 的 output 来学习。
- 也许你会问,teacher 的 output 是错的怎么办?不用管它,teacher 是错的,student 就按错的去学。
为什么不直接用正确答案来 train 一个小的 network 呢?因为往往直接训练小的 network 不如让它根据大的 network 来学习得到的效果好。就像上面例子中,输入的图片是手写的“1”,但让 small model 学它可能比较难,现在让它跟着 teacher 学,现在 teacher 也说他也分不太清这是不是 1,只是说 0.7 的概率是 1,但也有可能是 7,7 跟 1 还是有点像的。这样学出来的 student 反而比直接从正确答案学出来的效果好。
Knowledge Distillation 首先是在 paper (opens new window) 上提出的。
# 2.2 Knowledge Distillation 在 Ensemble 上的应用
Teacher Network 不一定是单一一个巨大的 network,它甚至可以是多个 Network 的 Ensemble。如下图所示:
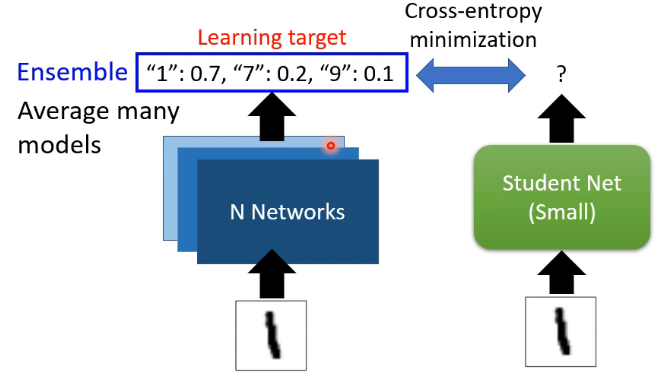
Ensemble 指训练多个 model,最终的结果由多个 model 进行投票来决定,或 average many models。
在实际应用中,Ensemble 多个 model 会导致计算量过大,那么我们就可以通过 Knowledge Distillation 来 train 一个 student network,从而让 student network 来逼近 Ensemble 多个 model 的 performance。
# 2.3 Temperature for softmax
这是做 Knowledge Distillation 的一个小技巧:Temperature for softmax:
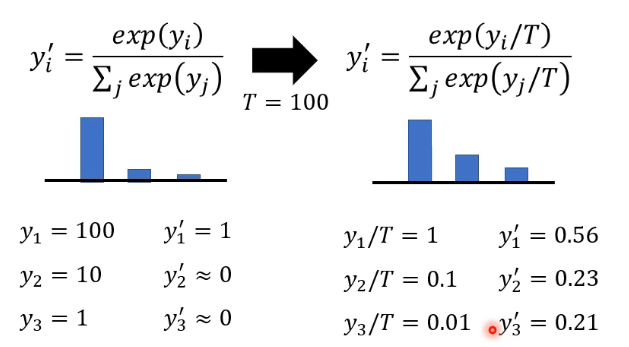
具体做法就是在做 softmax 前,每个 y 先除以一个 T,这个 T 是一个 hyper-parameter。 这样做可以使得将原先比较集中的分布变得比较平滑。为什么要这么做呢?举一个例子可以看到,当分布比较集中时,softmax 后的结果作为 output 和正确答案没什么差别了,这样 student 从 teacher 学和从答案学的基本一样了,原本 teacher 的好处就是能告诉 student 哪些类别是比较像,哪些是略微像,这样能让 student 学的不会那么辛苦。所有这里要加上一个 Temperature,而且对于 teacher 来说,加上 Temperature 后分类的结果不会变化,
# 3. Parameter Quantization
# 3.1 Parameter Quantization 的基本概念
- Using less bits to represent a value.
- Weight clustering
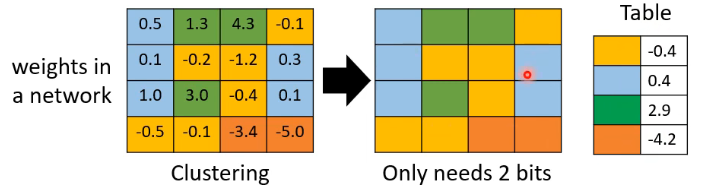
先设定一个 cluster 的数量(本例是 4),然后做 clustering,相近的数字会被当做是一个 cluster,之后,每个 cluster 只需要用一个数值来表示它。这样做的好处是,在存储你的参数时,只需要存储两样东西:一个记录每个 cluster 的代表数值的 table,一个是记录每个 parameter 是属于哪一个 cluster。
- Represent frequent clusters by less bits, represent rare clusters by more bits.
- e.g. Huffman encoding.
# 3.2 Binary Weights
到底可以压缩到什么程度呢?最终极的结果就是只拿 1 个 bit 来存每一个参数,这样,your weights are always +1 or -1,这就是 Binary Weights。具体做法的细节可以参考相关研究的 paper:
可能有人会觉得这样做的效果会很烂,但这未必。将一个经典方法 Binary Connect 用在了三个影像辨识上:
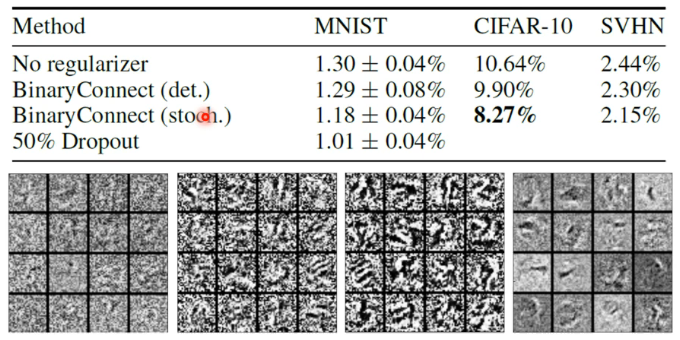
- 第一行是没有使用 Binary Weights 的 model
- 数值代表错误率,越小越好
可以看到,用了 Binary Connect 后,performance 居然比正常的 network 还要好一点。一个原因可能是 Binary Weights 给了 Network 比较大的限制从而使其不容易 overfitting。
# 4. Architecture Design - Depthwise Separable Convalution
# 4.1 Review:Standard CNN
我们先来回顾一下标准版的 CNN:
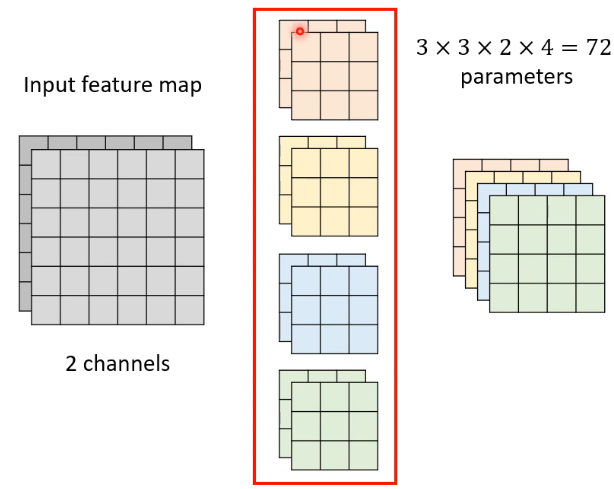
- Input feature map 有两个 channel,你的每个 filter 的高度就要是 2。【input channel number = filter height】
- 每个 filter 会得到另外一个 matrix,有几个 filter,得到的 output 就有几个 channel。【filter number = output channel number】
# 4.2 Depthwise Separable Convalution 的操作
我们先来看 Depthwise Separable Convalution 的操作,它的做法分成两个步骤:
# 👣 step 1:Depthwise Convolution
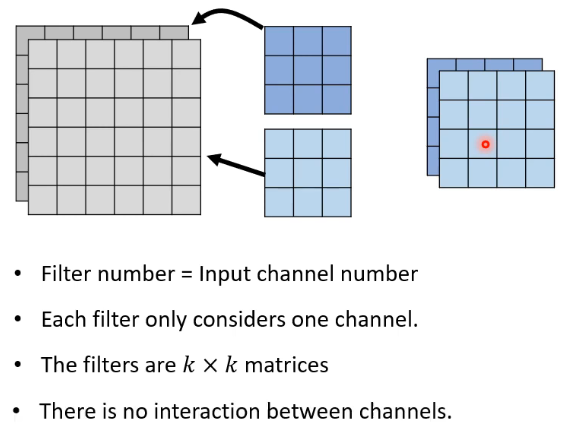
- 这种做法就是让一个 filter 去处理一个 channel 来得到一个 matrix output
- 有一个遇到的问题是:不同的 channel 之间没有任何互动了,这样就无法捕捉到跨 channel 的 pattern 了,所以需要再接一个 Pointwise Convolution
# 👣 step 2:Pointwise Convolution
Pointwise Convolution 的卷积做法与标准的 CNN 是一致的,只不过是将 filter 限制在 1 * 1 的大小上:
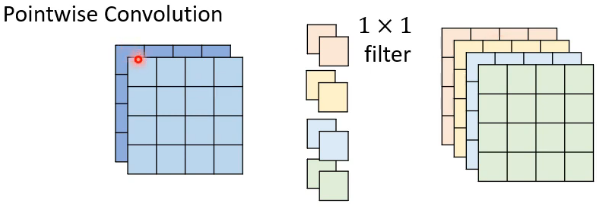
这一步所做的就是只考虑 channel 与 channel 之间的关系,而不考虑 channel 内部的关系了。
# 4.2.3 对比 standard CNN 与 Depthwise Separable Convalution
如下图所示,左边是 standard CNN,右边是 Depthwise Separable Convalution:
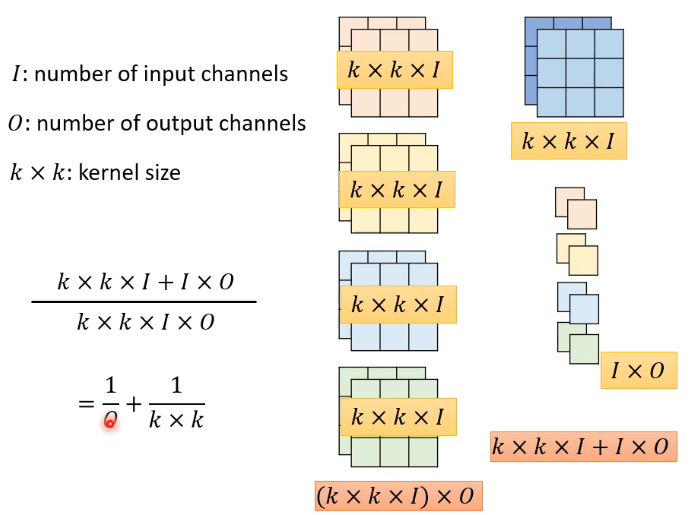
看一下两者参数量的比值,往往 O 是比较大的数值,因此主要看第二项
# 4.3 Low rank approximation
接下来解释为什么这一招是有用的。 这要提到 Low rank approximation:
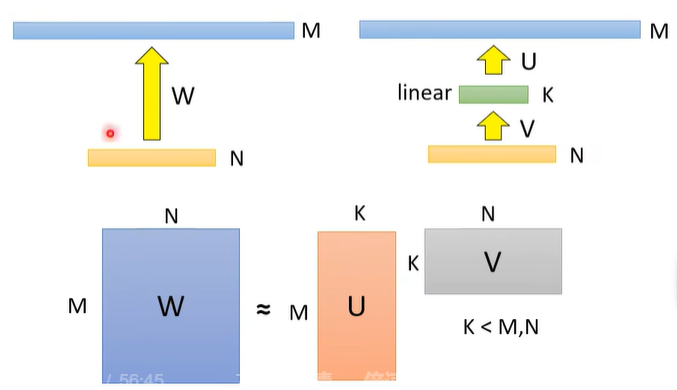
如图上面的左边,假如你有一个 layer,输入有 N 个 neuron,输出有 M 个 neuron,假设 N 或 M 其中之一非常大,那 W 的参数量
如果算一下会知道,如果插入的 linear 层的 K 远小于 M 和 N,那这个两层的 network 的参数量是小于一层 network 的参数量的。
这个方法虽然会减少参数量,但也存在一些 limitation。当把 W 拆解成 U V 之后,其 rank 是小于等于 K 的,所以这么做会缩小 W 所能取值的参数空间。
其实刚刚讲的 depthwise 和 pointwise 的 convolution 就是用的这个 Low rank approximation 的概念,就是将一层拆成了两层。如下图所示:
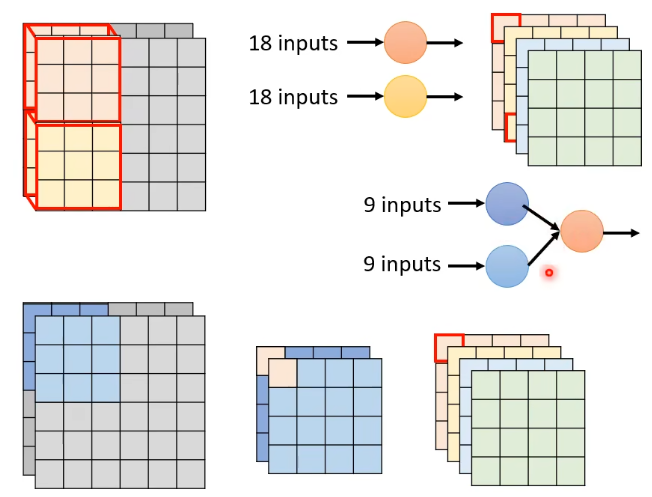
- 上面的是 standard CNN 做的,output 中的一个 value 是直接从 18 个 inputs 里得到的;
- 下面的则是 Depthwise Separable Convalution,它所做的是先 9 个 inputs 得到一个中间 value,然后两个中间 value 得到最终一个 output value。
To learn more...
# 5. Dynamic Computation
# 5.1 概述
Dynamic Computation 要做的是:The network adjusts the computation it need. 为什么要这么做呢?因为我们可能有不同的 device,他们的性能不一样,甚至对于同一个 device,在 high/low battery 的情况下我们想分配的计算资源也不一样。
Why don’t we prepare a set of models? 因为我们本来是要减少计算量,但这么做会需要很多的存储空间,所以这可能不是我们想要的,我们想要的是一个 network,它可以自由调节它对运算资源的需求。
# 5.2 Dynamic Depth
一个方向是能让 network 自由调整它的深度。具体做法如下:
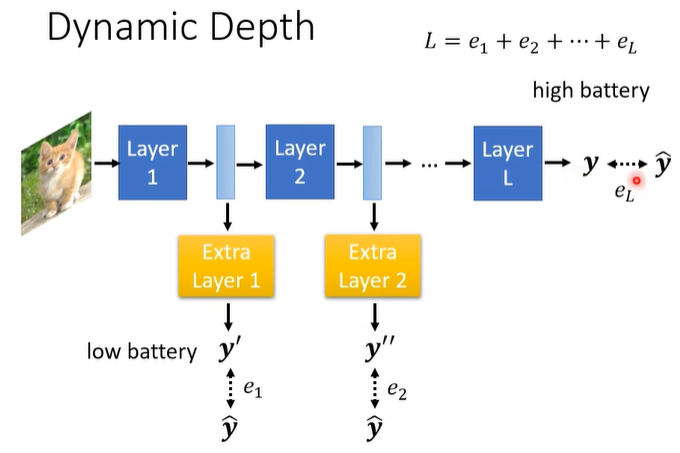
在一些层后面加上 Extra Layer,他们也用来预测答案。当 high battery 时就走完整个 network,当 low battery 时就走某个 extra layer。训练方式就是把这些损失全部加起来当成最终的 loss
这个方法好嘛?也可以做,但如果想要更好的结果,可以参考 MSDNet (opens new window) 这篇 paper。
# 5.3 Dynamic Width
设定好几个不同的宽度,把同一张 image 丢进去,每个不同宽度的 network 会有不同的输出,同时我们希望每个输出都是跟正确答案越接近越好:
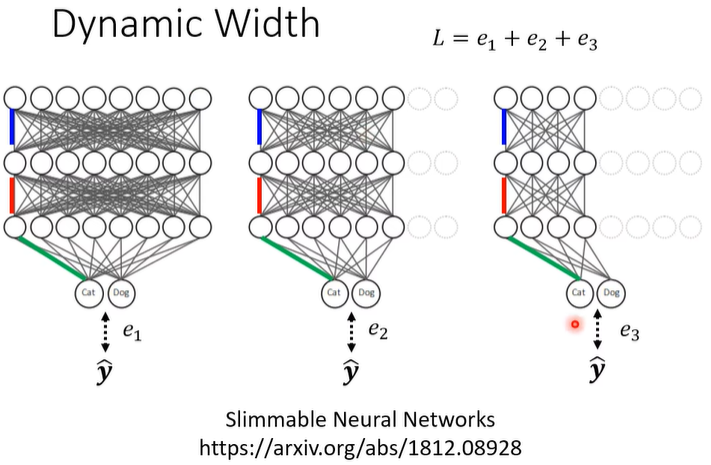
- 注意这里虽然画了三张图,但表示的都是同一个 network,比如三个图片中同一颜色的是同样的 weight。
# 5.4 Computation based on Sample Difficulty
刚刚我们讲的 network 可以自由去决定它的深度或宽度,但决定权还是在人这一边。那有没有办法让 network 自行决定根据它的环境来决定它的宽度或深度呢?这是有办法的。
为什么要这么做呢?以影像分类为例,有的 image 可能很简单,但有的可能很难,简单的 image 只需要一个 layer 就分出来了,而困难的可能需要很多 layer 才能找到答案:
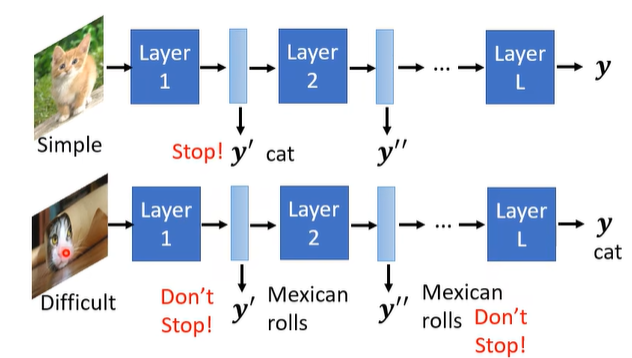
具体的做法可以参考下面的 paper:
- SkipNet: Learning Dynamic Routing in Convolutional Networks
- Runtime Neural Pruning
- BlockDrop: Dynamic Inference Paths in Residual Networks
Concluding Remarks
- Network Pruning
- Knowledge Distillation
- Parameter Quantization
- Architecture Design
- Dynamic Computation
