• 1. Deep Learning
  • 1.1 Different types of Functions
  • 1.2 Case Study
  • 1.3 分段线性曲线
  • 1.4 回到 ML-Step2：define loss from training data
  • 1.5 回到 ML-Step3：Optimization
  • 1.6 模型变形
  • 1.7 多做几次
  • 1.8 给他们起个名字

1. Deep Learning

先简单介绍一下 machine learning 还有 deep learning 的基本概念。机器学习就是让机器具备找一个函式的能力。

函式即 function，也就是常说的函数。

1.1 Different types of Functions

• Regression：要找的函式的输出是一个 scalar，即数值
• Classification：就是要机器做选择题
• Structured Learning：让机器画一张图，写一篇文章，这种叫机器產生有结构的东西的问题就叫作 Structured Learning

1.2 Case Study

机器怎么找一个函式呢？举一个例子，在 YouTube 后台，你可以看到很多相关的资讯，比如说每一天按讚的人数有多少，每一天订阅的人数有多少，每一天观看的次数有多少。我们能不能够根据一个频道过往所有的资讯去预测它明天有可能的观看的次数是多少呢，我们能不能够找一个函式，这个函式的输入是我 YouTube 后台的资讯，输出就是某一天，隔天这个频道会有的总观看的次数。

机器学习找这个函式的过程，分成三个步骤，那我们就用 YouTube 频道点阅人数预测这件事情，来跟大家说明这三个步骤，是怎么运作的：

1）Function with Unknown Parameters

第一个步骤是我们要写出一个带有未知参数的函式。简单来说就是 我们先猜测一下,我们打算找的这个函式,它的数学式到底长什麼样子。举例来说，我们这边先做一个最初步的猜测，我们写成这个样子：，其中：

• y 是我们準备要预测的东西，我们準备要预测的是今天 2 月 26 号这个频道总共观看的人；
• 是这个频道前一天总共观看的人数， 跟 都是数值；
• b 跟 w 是未知的参数，它是准备要透过资料去找出来的，我们还不知道w跟b应该是多少,我们只是隐约的猜测

这个猜测往往就来自于你对这个问题本质上的了解，也就是 Domain knowledge，所以才会听到有人说,这个做机器学习啊，就需要一些 Domain knowledge。

我们就随便猜说 ₗ，而 b 跟 w 是未知的，这个带有 Unknown 的 Parameter 的 Function 我们就叫做 Model。这个 是这个 function 里面我们已知的，它是来自于 YouTube 后台的资讯，我们已经知道2月25号点阅的总人数是多少，称之为 Feature。

2）Define Loss from Training Data

第二个步骤我们要定义一个 Loss。Loss 也是一个 function，输入是 Model 里面的参数，输出的值代表说，现在如果我们把这一组未知的参数，设定某一个数值的时候，这笔数值好还是不好。比如例子中 、 就是 Loss 的输入。Loss 要从训练样本中进行计算，计算结果为 L，大 L 越大，代表我们现在这一组参数越不好，这个大 L 越小，代表现在这一组参数越好。

估测的值跟实际的值之间的差距，其实有不同的计算方法。比如 MAE、MSE 以及 Cross-Entropy 等。

为不同的 w 跟 b 的组合，都去计算它的 Loss，然后就可以画出以下这一个等高线图，称为 Error Surface：

• 越偏红色系，代表计算出来的Loss越大，就代表这一组 w 跟 b 越差，如果越偏蓝色系，就代表 Loss 越小，就代表这一组 w 跟 b 越好。

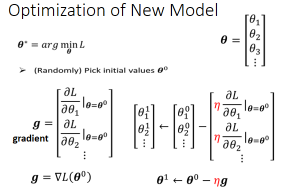
3）Optimization

第三步要做其实是解一个最佳化的问题。在这个例子中就是找一个 w 跟 b，从未知的参数中找一个数值出来，代入后可以让 Loss 值最小。在这一门课里面，我们唯一会用到的 Optimization 的方法叫做 Gradient Descent。

为了要简化，我们先假设未知的参数只有一个 ，得到其 Error Surface：

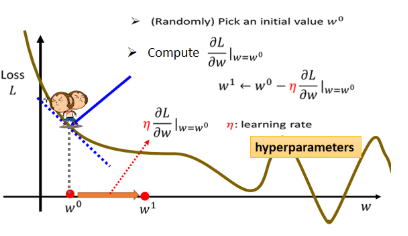
那怎样找一个 w 让这个 loss 的值最小呢？随机选取一个初始的点，这个初始的点,我们叫做 -> 求参数对 Loss 的微分 -> 更新参数值。更新时这一步要跨多大呢？这一步的步伐的大小取决于这个地方的斜率和学习率 ()。

什么时候停下来呢？往往有两种状况：

• 第一种状况是你失去耐心了，你一开始会设定说，我今天在调整我的参数的时候，我最多计算几次；
• 那还有另外一种理想上停下来的可能是，今天当我们不断调整参数时调整到一个地方，它的微分的值算出来正好是 0 的时候，如果这一项正好算出来是0.0乘上 learning rate 还是 0，所以你的参数就不会再移动位置，那参数的位置就不会再更新。

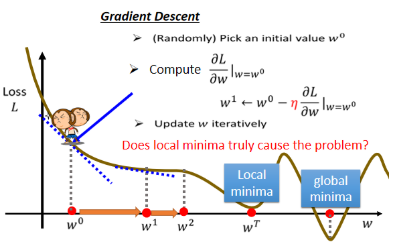
你可能会发现 Gradient Descent 这个方法有一个巨大的问题，我们没有找到真正最好的解，我们只是找到的 local minima 而不是 global minima。其实，local minima 是一个假问题，我们在做 Gradient Descent 的时候真正面对的难题不是 local minima，之后会讲到它的真正痛点在哪。

刚刚只有一个参数 w，将其扩展至二维乃至多维是同理。

1.3 分段线性曲线

Linear 的 Model 也许太过简单了，对 Linear 的 model 来说，x1 跟 y 的关係就是一条直线，这也就是说前一天观看的人数越多，隔天的观看人数就越多，但也许现实并不是这个样子，不管怎么摆弄 w 和 b，你永远制造不出一个不完全线性（或带有分段）的一个函数曲线，显然 Linear 的 Model 有很大的限制，这一种来自于 model 的限制，叫做 model 的 Bias。所以我们需要写一个更复杂的，更有弹性的，有未知参数的 Function。

这里 “model 的 bias” 和 y = wx + b 中 b 这个 bias 是不一样的，model 的 bias 是说没有办法模拟真实的状况。

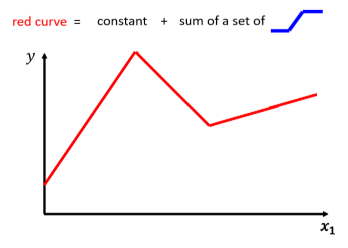
我们可以观察一下这个红线，它可以看做是一个常数，再加上一群蓝色的曲线组合而成的 function：

怎样让蓝色曲线通过变化组合成红色的曲线呢？

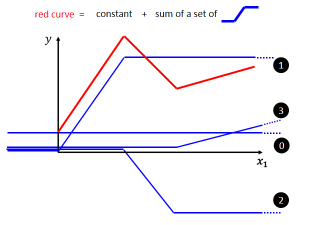
蓝线“1”Function 斜坡的起点,设在红色 Function 的起始的地方,然后第二个,斜坡的终点设在第一个转角处,你刻意让这边这个蓝色 Function 的斜坡,跟这个红色 Function 的斜坡,它们的斜率是一样的,这个时候如果你把 0 加上 1,你就可以得到红色曲线

然后接下来,再加第二个蓝色的 Function,你就看红色这个线,第二个转折点出现在哪裡, 所以第二个蓝色 Function,它的斜坡就在红色 Function 的第一个转折点,到第二个转折点之间,你刻意让这边的斜率跟这边的斜率一样,这个时候你把 0加 1+2,你就可以得到两个转折点这边的线段,就可以得到红色的这一条线这边的部分

然后接下来第三个部分,第二个转折点之后的部分,你就加第三个蓝色的 Function,第三个蓝色的 Function,它这个坡度的起始点,故意设的跟这个转折点一样,这边的斜率,故意设的跟这边的斜率一样,好 接下来你把 0加 1+2+3 全部加起来,你就得到红色的这个线。

所以红色这个线,可以看作是一个常数,再加上一堆蓝色的 Function

类似，对于光滑曲线可以将其分成若干点，这些点就可以组成一个接近于光滑曲线的分段线性曲线，然后再用一群蓝色曲线去拟合。

所以我们今天知道一件事情，你可以用分段线性曲线去逼近任何的连续的曲线，而每一个分段线性曲线又都可以用一大堆蓝色的 Function 组合起来，也就是说，我只要有足够的蓝色 Function 把它加起来，也许就可以变成任何连续的曲线。

但这个蓝色曲线怎么写出来呢？我们可以使用 Sigmoid 的 function 来作为这个蓝色 function。

Sigmoid

非线性 sigmoid 函数（常简写为 sigm）：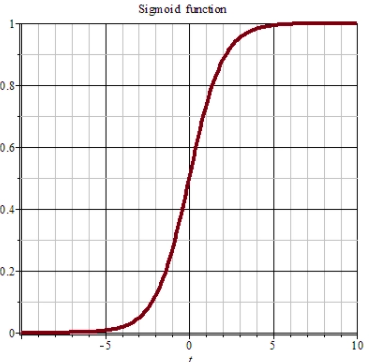

• 助记：Sigmoid 可以记成 S 函数，因为它的图像很像一个大 S。

对 Sigmoid 做各种变化（拉长、上移等）后，可以用下面这个公式表达：

各种变化后的 function 如下图：

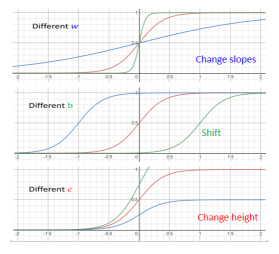
• 如果改 你就会改变斜率
• 如果你动了 你就可以把这一个 Sigmoid Function 左右移动
• 如果你改 你就可以改变它的高度

那我们把之前那条红色曲线的函数写出来，可能会长成：

利用这个形式，我们就可以突破之前 Linear Model 的限制，即减少 Model 的 Bias。于是对之前的 model 做以下改变：

但这只是一个 feature ，如果有多个 feature 呢？我们假设用 j 来代表 features 的编号：

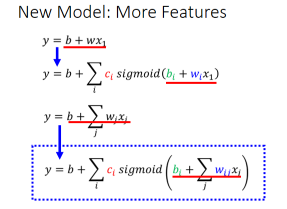
考虑一个实际的例子，只考虑有三个 feature，即 j=3，在之前的例子中，我们只考虑前一天、前两天和前三天的 Case 作为输入，即 x1 代表前一天的观看人数，x2 两天前观看人数，x3 三天前的观看人数。

Sigmoid 里面这部分的运算过程就是：

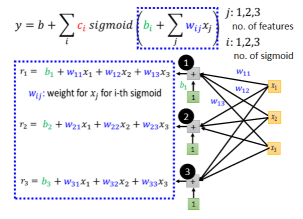
• j 表示 features，i 表示有几个 sigmoid 函数

把运算结果 进行整理可以得到：

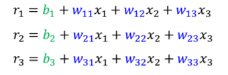
写成矩阵形式就是：

再经过 sigmoid 和 后得到：

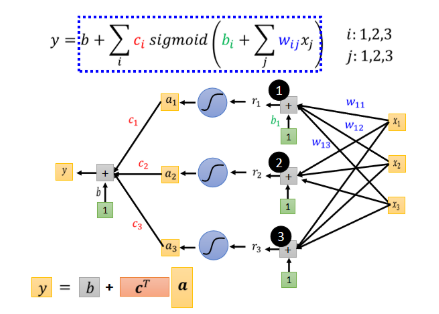
• 这里 ， 是 Sigmoid

最后我们可以得到如下公式：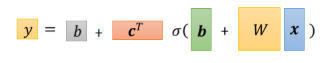

这里我们将未知参数合并起来统称为 。

1.4 回到 ML-Step2：define loss from training data

有了新的 model 以后，我们的 Loss 定义仍然相同，只是参数变了下，写成 。计算方法仍然与以前一样：

• 代入一组
• 把一种 feature 代入进去，然后看看估测的
• 计算一下估测值 与真实值 的差距，得到一个 e
• 把所有误差统统加起来，就可以得到 Loss：

1.5 回到 ML-Step3：Optimization

Optimization 思路与之前仍然相同：

batch 与 epoch 的概念

在实际中，假设我们有 N 笔资料，我们会将其分成一个一个的 Batch，分 B 笔资料为一组，一组叫做一个 Batch。

本来我们是把所有的 Data 拿出来算一个 Loss，现在我们不这么做，我们只拿一个 Batch 里面的数据出来算一个 Loss，对这个 Loss 算一次 Gradient 来 update 一次。

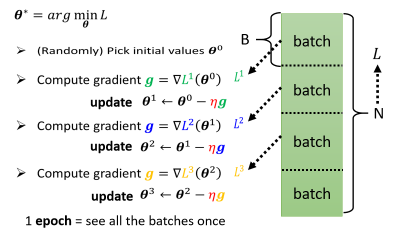
每次更新一次参数叫做一次 Update，把所有的 Batch 都看过一遍,叫做一个 Epoch。至于为什么要这么分，我们下节再讲。

Example

Example 1：

• Q：10,000 examples（N = 10,000），Batch size is 10（B = 10）。How many update in 1 epoch？

• A：1,000 updates

Example 2：

• Q：1,000 examples（N = 1,000），Batch size is 100（B = 100）。How many update in 1 epoch？

• A：10 updates

所以做了一个 Epoch 的训练,你其实不知道它更新了几次参数,有可能 1000 次,也有可能 10 次，取决于它的 Batch Size 有多大。

1.6 模型变形

刚刚我们用的 Soft Sigmoid 来当成小蓝色曲线，但也可以用其他的，比如两个 Rectified Linear Unit（ReLU） 可以组合成一个 Hard Sigmoid：

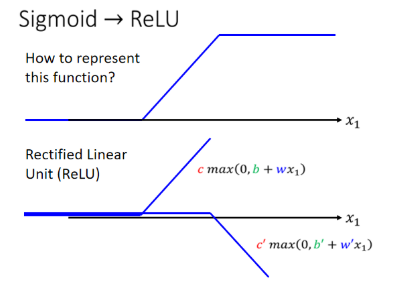
所以要表示这个蓝色曲线不只有一种做法，完全可以用其他的做法，他们统称为 Activation Function。到底用哪个好，之后再讨论。

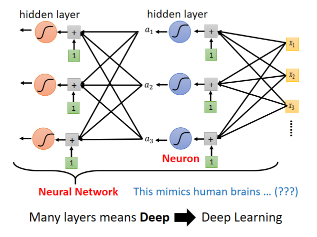
1.7 多做几次

我们刚刚从 x 到 a 要做的事情是：把 x 乘上 w 加 b，再通过 Sigmoid Function。我们可以把这个同样的事情，再反覆地多做几次，如图：

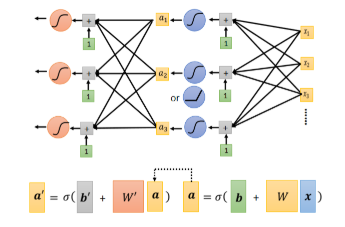
这个过程做几次呢？这又是一个 Hyper Parameter。

实验结果：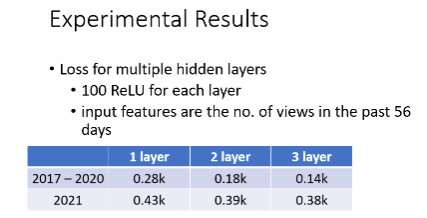

1.8 给他们起个名字