Self-Attention

Self-Attention 是一个很常见的 Network 架构。

# 1. 引言

之前我们的 model 的输入是一个向量，输出可能是一个数值，这是 Regression，还可能是一个类别，这是 Classification。

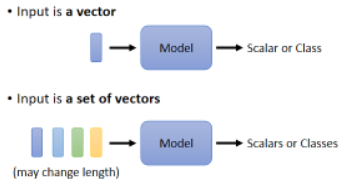
假设我们遇到更复杂的问题，比如输入是多个向量，且输入的向量数目会改变。现在如果我们 model 输入的 sequence 的数目、长度都不一样，这时该如何处理？

# 1.1 Vector Set as Input

# 1）文字处理

假设我们今天要Network的输入是一个句子,每一个句子的长度都不一样,每个句子裡面词汇的数目都不一样, 如果我们把一个句子裡面的每一个词汇都描述成一个向量,那我们的Model的输入,就会是一个Vector Set,而且每次句子的长度不一样,那 Vector Set 的大小就不一样：

那怎么把词汇表示成一个向量呢？最简单的是 one-hot encoding，还有一种方法是 Word Embedding，形成单词的分布式表示。

# 2）声音信号

一段声音讯号其实是一排向量，把一段声音讯号取一个范围，这个范围叫做一个 Window，每个 Window 里面得资讯描述成一个向量，这个向量就是一个 Frame：

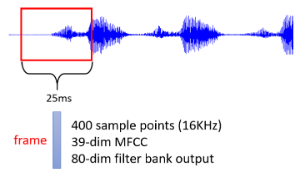
把一小段声音讯号变成一个 Frame，有很多种做法，这里不再细讲了。

通常 Window 的长度是 25 个 Millisecond，为了描述一整段声音讯号，我们会把这个 Window 右移一点，通常移动的大小是 10 个 Millisecond：

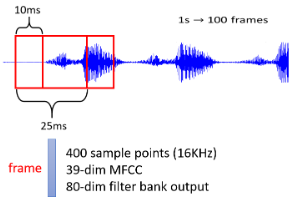
一秒钟声音讯号就有 100 个向量，一分钟声音讯号有 6000 个向量，所以语音其实还是挺复杂的。

# 3）图

一个 Graph 也是一堆向量。在 Social Network 上面每个节点是一个向量，关系可以视为向量。

# 4）分子信息

一个分子也可以看作是一个 Graph：

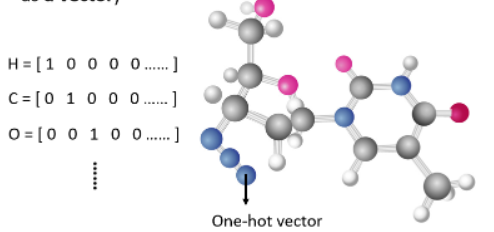
一个原子可以用 One-Hot Vector 来表示，比如氢就是 1000，碳是 0010 等。

# 1.2 What is the output?

刚才看到输入是一堆向量，那我们有可能有什么样的输出呢？

# 1）每一个向量都有一个对应的 Label

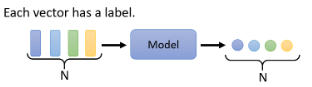
当你的模型的输入是四个向量的时候，它就要输出四个 Label，而

若每个 Label 是一个数值，那就是 Regression 的问题
若每个 Label 是一个类别，那就是 Classification 的问题

应用举例：

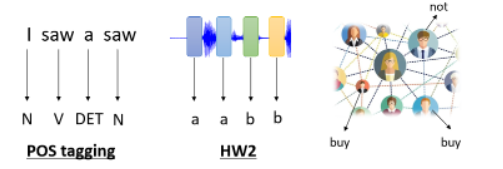
POS Tagging，即词性标注，让机器自动决定每一个词汇的词性，是名词、动词还是形容词等
语音辨识，对每一个 vector，来辨识它是哪一个 Phonetic
在 Social Network 中，你的 model 来决定每一个节点的特性，比如他会不会买某个商品

# 2）一整个 Sequence，只需要输出一个 Label

比如 Sentiment Analysis（情感分析），给机器看一段话，判断他是正面还是负面的；比如语音辨认，给机器听一段语音，然后判断是谁讲的；比如在 graph 领域，给一个分子，然后预测它有没有毒性等

# 3）机器要自己决定应该要输出多少个 Label

这种任务又叫做 seq2seq。

# 1.3 Sequence Labeling

这种输入跟输出数目一样多的状况又叫做 Sequence Labeling，我们着重研究这个问题。

解决这个问题的一个简单想法是用 Fully-Connected（简称 FC）的 Network：

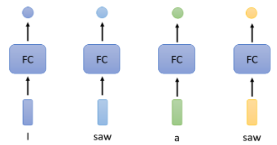
但这样有一个巨大的瑕疵，它无法识别出不同语境下“saw”的不同，它有“看见”、“锯子”的意思。怎么办才有可能让 Fully-Connected 的 Network 考虑更多的上下文 context 的资讯呢？

这时有可能的，只需要把前后几个向量都串起来，一起丢到 FC 的 network 中就行了：

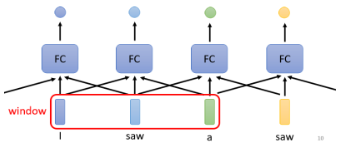
但这样总是有极限的，比如一个任务不是考虑一个 Window 就可以解决的，而是要考虑一整个 Sequence 才能够解决的话，就只能再把 Window 开大一点直到能覆盖整个 sequence。但是这么大的 Window，意味着 FC 的 network 需要非常多的参数，运算量大且容易 overfitting。

所以有没有更好的方法来考虑整个 Input Sequence 的资讯呢？这就要用到我们接下来要跟大家介绍的 Self-Attention 这个技术了。

# 2. Self Attention

# 2.1 self attention 概述

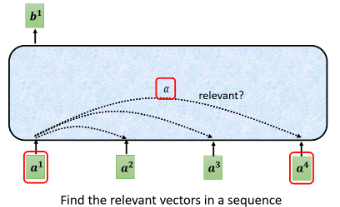
Self-Attention 的运作方式就是它会吃一整个 Sequence 的资讯。

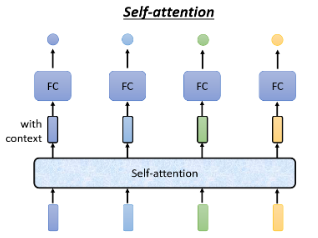
Self Attention 中 input 几个 vector 就输出几个 vector，这里输出的 4 个 vector 有个特别的地方：它们都是考虑一整个 Sequence 以后才得到的。等一会我们会讲 Self-Attention 怎么考虑到一整个 Sequence 的资讯的。

Self-Attention 输出的向量是 with context 的，这样一来 FC 的 Network 就不只是考虑一个非常小的 Window 了，而是一整个 Sequence 的资讯，再决定应该输出什么样的结果，这个就是 Self-Attention。

Self-Attention 不是只能用一次，也可以叠加很多次，可以把 Fully-Connected 的 network 跟 self attention 交替使用：

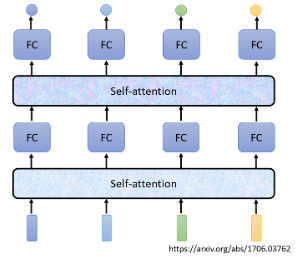
Self-Attention 处理整个 Sequence 的资讯
FC 的 Network 专注于处理某一个位置的资讯
再用 Self-Attention 把整个 Sequence 资讯再处理一次
然后交替使用 Self-Attention 跟 FC

有关 self attention，最知名的文章就是《Attention is all you need》，它提出了 Transformer 的 Network。

# 2.2 self attention 过程

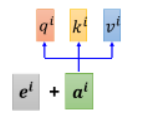
Self-Attention 的 input 是一串的 vector，这个 vector 可能是整个 Network 的 input，也可能是某个 hidden layer 的 output，所以我们这边不是用来表示它，而是用来表示。self attention 的 output 是另一排的 vector 。

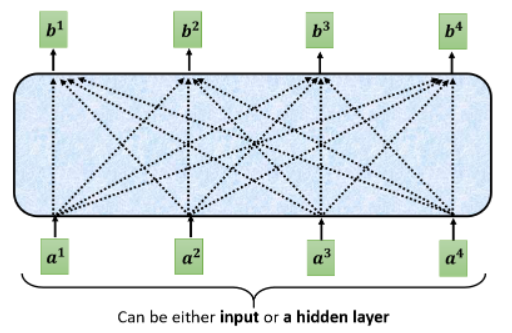
每一个都是考虑了所有的才生成出来的，所以刻意画了非常非常多的箭头

接下来我们说明一下怎样产生这个向量，由此就可以知道怎样产生另外的几个了。

这里有个特别的机制：这个机制根据这个向量，找出整个 sequence 里到底哪些部分是重要的，哪些部分是我们要决定的 class 或 regression 数值的时候所需要用到的资讯。每一个向量跟的关联程度用一个数值表示：

那如何自动计算两个向量之间的关联性呢，即如何计算两个向量之间的数值呢？这需要一个计算 attention 的模组：

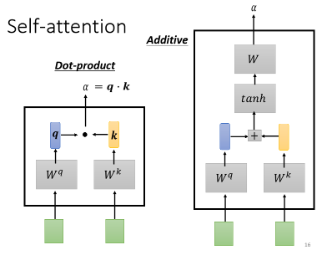
这个计算 attention 的模组就是拿两个向量作为输入，输出。我们常用的是左边 Dot-product 的做法：

输入的这两个向量分别乘上两个不同的矩阵，得到和
和做 dot product 得到一个 scalar，这个 scalar 就是

还有其他许多计算 attention 的模组，之后我们只用上图左边的那种，它也是最常用的。

上图计算过程中的 vector 叫做 Query，vector 叫做 key，它们的上标与输入向量的上标相同，比如 self-attention 的输入向量计算得到的是和。

用来表示两个向量的关联性的叫做 attention score，用作为其下标的含义，这样计算各 attention score 的过程如下图：

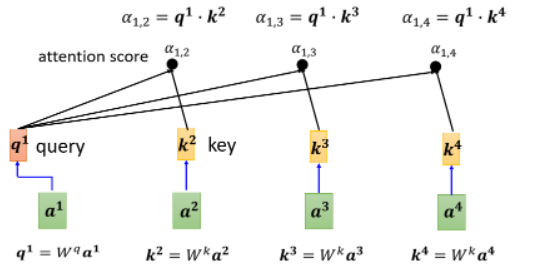
实际情况下，一般也会让与自己算关联性。计算出跟每一个向量的关联性以后，接下来进入一个 softmax：

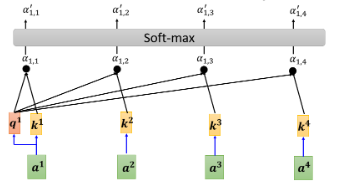
本来有一排的，经过 softmax 后就得到
不一定非要用 softmax，用别的替代也没问题，换其他的 activation function 都可以，这需要手工调试一试

得到后就可以根据它去抽取出 sequence 里面重要的资讯。由可以知道哪些向量跟最有关系，那怎样抽取重要的资讯呢？

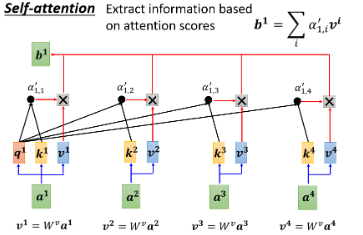
将与相乘得到
各乘上 attention score
再累加起来得到：

如果某一个向量它得到的分数越高，比如说如果与的关联性很强，那这个得到的的值就很大，那我们做 weight sum 以后，得到的的值就可能会比较接近。所以谁的那个 attention score 最大，谁的那个就会 dominant 你抽出来的结果。

以上就讲完了如何从一整个 Sequence 里得到。

# 2.3 矩阵的角度看 self-attention 的运行

我们再从矩阵乘法的角度重新看一遍 self-attention 是怎样运行的。

现在我们已经知道每一个都产生、、，即：

这样写成矩阵的形式，把、、、视为矩阵，同样将所有视为矩阵，于是得到：：

、的操作跟是一样的，类比可以写出：

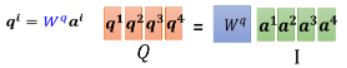
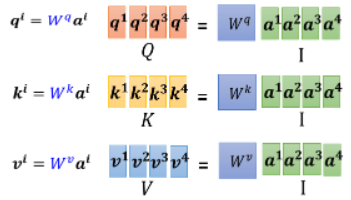
我们再看 attention score 的计算，之前的计算过程可以绘制为：

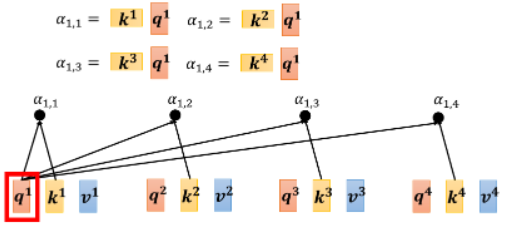
比如与做 inner product 得到

上面四个步骤的操作可以拼接起来，视为一个矩阵与向量相乘：

~ 可以视为一个矩阵的四个 row

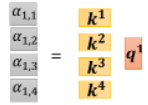
现在不只是对计算 attention，还对 ~ 都计算，而且它们都是要对 ~ 做相同的操作，于是可以继续合并为：

所以 attention score 的计算可以视为两个矩阵的相乘

我们再来复习一下，整个 self attention 运行过程就是：

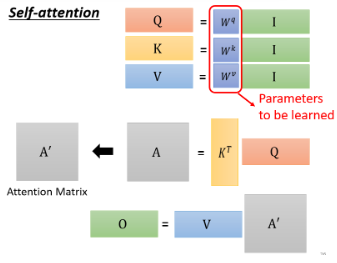
可以看到，在这个 self-attention layer 中唯一需要学习的参数就是、和，只有他们是未知的。

上面的从到就是 self-attention。

# 2.4 Multi-head Self-attention

Self-attention 有一个进阶的版本，叫做 Multi-head Self-attention。在一些任务中，比如语音识别，用较多的 head 可以得到比较好的结果。至于用多少个 head，这又是一个 hyperparameter。

为什么我们需要比较多的 head 呢？我们在做 self attention 时，是用 q 去找相关的 k，但**“相关”这件事情可能有很多种不同的形式**。所以也许我们不能只有一个 q，而是应该有多个 q，不同的 q 负责不同种类的相关性：

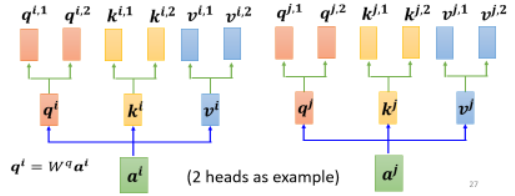
先把乘上一个矩阵得到
再把乘上两个矩阵，分别得到和，这里上标中的 1、2 代表说有 2 个 head

我们认为要解决的问题里面有两种不同的相关性，于是我们需要两个 head，来找这两种不同的相关性。

既然有两个，那、也自然有两个。每一个 head 在计算时，与之前的 self-attention 计算过程完全一样，不会与其他 head 产生交集。最终，head 1 产生，head 2 产生：

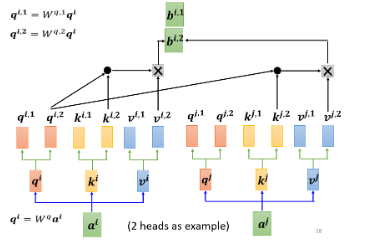
得到和后，你可能会把他们接起来，再乘上一个矩阵得到：

最终将送到下一层去。以上就是 Multi-head self-attention。

# 3. Positional Encoding

到目前为止，你会发现 self-attention layer 少了位置的资讯。这就是说，位置 1 和位置 2、3 完全没有任何差别。但位置的资讯又是比较重要的，比如在词性标注（POS tagging）中，动词不太容易出现在句首。

下面讲解一种解决方案：

# 3.1 Each positon has a unique positional vector

在做 Self-attention 的时候，如果你觉得位置的资讯是一个重要的事情，那可以想办法把位置的资讯塞进去，这需要用到 Positional Encoding 的技术。

可以为每个位置设定一个 vector，叫做 positional vector，用表示，上标 i 代表位置，每一个不同的位置有不同的 vector ，然后把这个加到上面就结束了：

这样做其实就是告诉 self-attention 位置的资讯，如果它看到好像有被加上，它就知道现在出现的位置应该是在 i 这个位置。

# 3.2 Hand-crafted or Learned from data

在《Attention is all your need》这篇 paper 中，它用的长这个样子：

每一个 column 代表一个

像这样的 positional vector 是 handcrafted 的，但这个人设的 vector 有很多问题，比如我现在在定 vector 的时候，定到了 128，但之后出现一个 Sequence 的长度是 129 就没办法了。不过在《Attention is all your need》中，它的 vector 是透过某一个规则来产生的，是透过一个神奇的 sin、cos 的 function 产生的。

其实不一定要这样产生，positional encoding 仍然是一个尚待研究的问题。你可以创造自己新的方法，甚至 positional encoding 是可以根据资料学出来的。

有关 positional encoding，可以参考一下这个文献 (opens new window)，这里面提出了新的 positional encoding 方法。

# 4. Application

self-attention 应用很广，在 NLP 中你肯定听到过 Transformer 和 Bert：

但 Self-attention 不是只能用在 NLP 相关的应用上，它还可以用在很多其他的问题上。

# 4.1 Self-attention for Speech

对于一般的语音，如果你要把一段声音讯号表示成一排向量的话，这排向量可能会非常地长，这个可观的长度会使得在计算 attention matrix 的时候产生性能问题，因为这一步的计算复杂度是长度的平方。这时不容易训练的，怎么办呢？

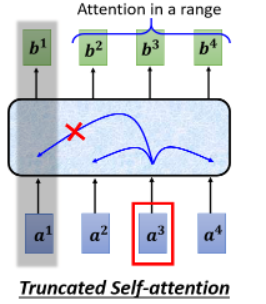
在做语音的时候，有一招叫做 Truncated Self-attention：我们在做 self-attention 的时候，不要看一整句话，就只看一个小的范围就好。因为在语音辨识时，只需要前后一定范围之内的资讯，其实就可以判断这个位置有什么样的 phoneme 或内容。

# 4.2 Self-attention for Image

我们在讲 Self-attention 的时候，都说它适用的范围是：输入是一个 vector set 的时候。而一张图片，换一个观点，也可以把它看作是一个 vector 的 set：

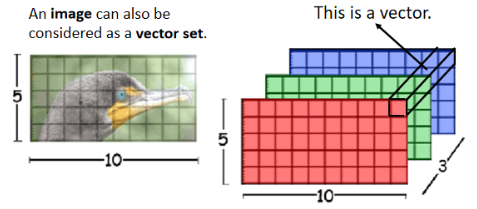
每一个 pixel 就是一个三维的 vector，整张图片就是有 5 × 10 个 vector 的 set

其实你可以读一篇 paper，叫做 On the Relationship,between Self-attention and Convolutional Layers，它用严谨的数学的方式来告诉了我们，CNN 就是 self-attention 的特例，只要设定合适的参数，self-attention 可以做到跟 CNN 一模一样的事情。所以 self attention 相比 CNN 更加 flexible。

既然 self-attention 比 CNN 更加 flexible，那就需要更多的 data，如果 data 不够的话就可能 overfitting。来看这个实验结果：

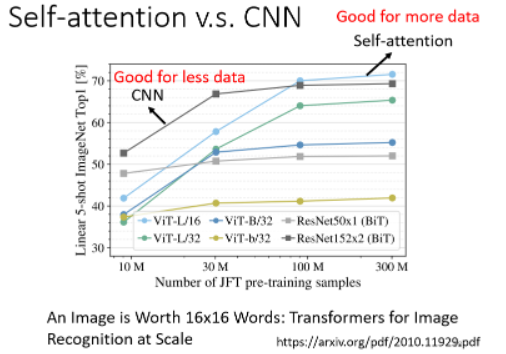
可以发现，随着资料量越来越多，Self-attention 的结果就越来越好，最终在资料量最多的时候 Self-attention 可以超过 CNN。但在资料量少的时候，CNN 它是可以比 Self-attention 得到更好的结果的。

# 4.3 Self-attention v.s. RNN

RNN 无法并行化运算，这是它的最大缺点，现在 RNN 的角色很大一部分都可以用 Self-attention 来取代了。这里不再展开。

# 4.4 Self-attention for Graph

Graph 也可以看作是一堆 vector，这样就可以用 Self-attention 来处理。其实当我们把 Self-attention 按照图的限制用在 Graph 上面的时候，其实就是一种 Graph Neural Network，也就是一种 GNN。

# 4.5 More

其实 Self-attention 有非常非常多的变形，你可以看一篇 paper，叫做 Long Range Arena，里面比较了各种不同的 Self-attention 的变形。因为 Self-attention 最大的问题就是它的运算量非常地大，所以怎样减少 Self-attention 的运算量是一个未来的重点。

self-attention 最早用在 Transformer 上，有人说广义的 Transformer 指的就是 Self-attention，以至于后来各种变形都这么做，所以 Self-attention 的变形，现在都叫做 xxformer。

现在很多新的 xxformer 的速度比 Transformer 快，但随之而来的是 performance 变差。到底什么样的 Self-attention 才能够真的又快又好，这仍然是一个尚待研究的问题。如果想要对 self attention 进一步研究的话，可以参考 Efficient Transformers: A Survey 这篇 paper，里面介绍了各式各样 self-attention 的变形。

编辑

上次更新: 2022/10/03, 13:55:17

← CNN 各式各样的 Attention→