1. self-attention 的问题

1.1 复习一下 self-attention

假设 sequence length = N，那么一次计算中会有 N 个 key，N 个 query，两两做 dot-product 产生一个 N * N 的 Attention Matrix：

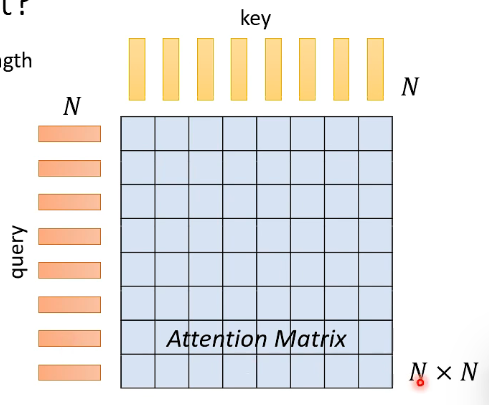
拿到 Attention Matrix 后，对 value vector 做 weight sum 就可以了。

而 self-attention 的痛点在于：计算 N * N 的 Attention Matrix 的计算量可能非常惊人，尤其是 sequence length N 非常长时。

1.2 Notice

• Self-attention is only a module in a larger network.
• Self-attention dominates computation when N is large in Transformer. 所以当 N 不是很大时，可能整个 network 受 feed forward 等其他 module 的 dominate，此时改进 self-attention 的效果也许对加快整体的训练不会有太大改进。
• Usually developed for image processing. 因为假如要处理一个 256 * 256 的 image，那此时 N = 256 * 256，计算量将非常大。

下面就要讲对 Self-Attention 的改进了。

2. Skip Some Calculations with Human Knowledge

idea：在计算 Attention Matrix 时，也许我们不需要计算每一个值，也许我们可以凭借 human knowledge 来预先填上一些值。

2.1 Local Attention / Truncated Attention

一种想法是，有些情况在做 Attention 的时候，有些位置不需要看整个 sequence，而是只需要看左右邻居就可以理解一个位置的 token 存有什么样的资讯：

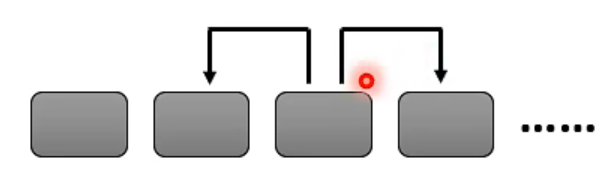
这样的话，我们可以直接把更长距离的 attention weight 设为 0，即：

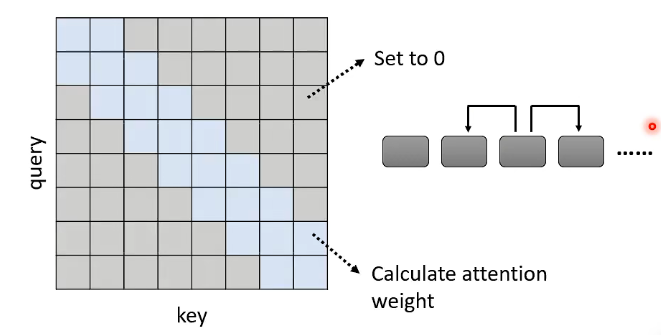
• 灰色部分直接被设为 0
• 蓝色部分才需要去计算 attention weight

上面这种方法称为 Local Attention / Truncated Attention。但这存在一个问题：每次做 attention 时只能看得到周围一小个范围的资讯，那这样的话就会跟 CNN 很像了。这种方式会加快你的运算，但不一定会带来好的结果。

2.2 Stride Attention

既然说只看邻居不好，那我们就看一下远一点的邻居：

• 在这里，我们先跳两格，看三格位置处的资讯，这样就可以看到更大的范围的资讯，把 Attention Matrix 网格画出来的话就是这样（灰色设为 0，青色才需要计算）：

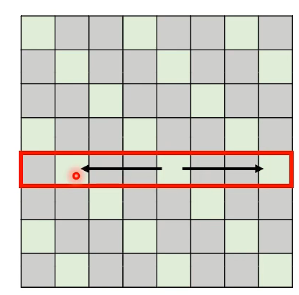
这种方式称为 Stride Attention。上面例子是空两格，当然也可以空一格、空三格 ….

2.3 Global Attention

刚刚所说的是只能知道周围发生了什么事，但如果想知道一整个 sequence 发生了什么事情，就需要用 Global Attention。

这需要在原来的 sequence 上加一些 special token，这些 special token 代表这些 position 需要做 Global Attention。

Global Attention 会做两件事：

• Attend to every token.（也就是从 sequence 的每一个 token 里面收集资讯） --> collect global information.
• Attended by every token. （也就是所有 token 都去看一下这个 special token 发生了什么资讯） --> it knows global information.

Global Attention 有两种做法：

• 直接在 original sequence 中 assign 一些 token 作为 special token。比如将作为开头 token 的 [CLS] 作为 special token，或将句号作为 special token。【如下左图】
• 外加一些额外的 token 作为 special token，这样不管 original sequence 是什么，都硬插几个 token 作为 special token。【如下右图】

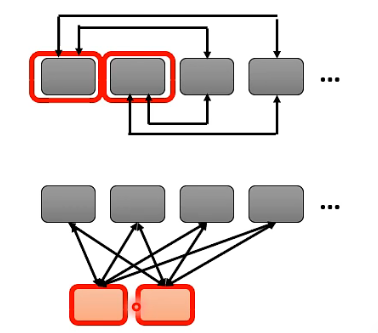
如果将 Attention Matrix 画出来的话，就会是下图这样：

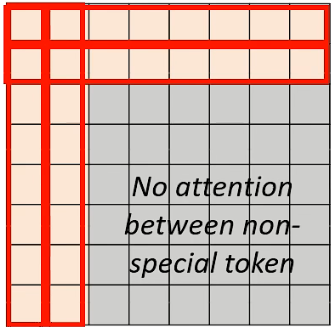
• 每一个 row 代表一个 query，每一个 column 代表一个 key
• 会发现前两个 row 都是有值的，也就是都是要做 attention 的，即前两个位置代表 special token，他们的 query 要被 attend 到所有其他人的 key 上；
• 前两个 column 也都是有值的，代表说除了 special token 以外的那些 token 在做 attention 的时候，他们的 query 都会被 attend 到前两个位置的 token 上；
• 除了前两个 token 会 attend 到其他所有人，也会被其他所有人 attend 以外，其他的 token 之间就彼此就没有往来了。

2.4 选择哪一种 self-attention？

上面讲了多种 self-attention 的改进方式，那选择哪一种最好呢？

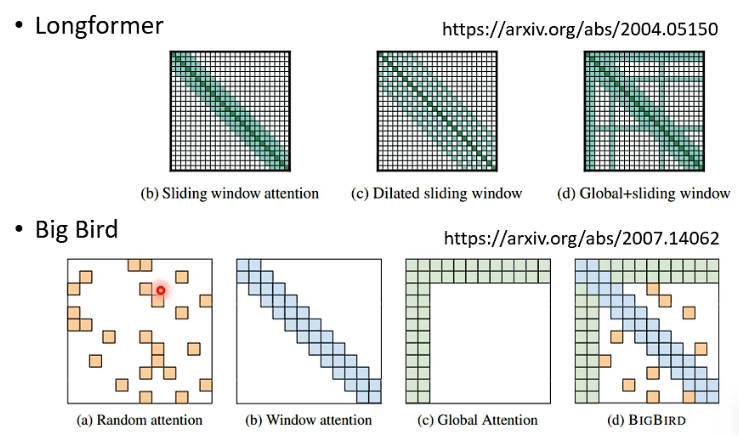
小孩子才做选择… Different heads use different patterns. 比如一些经典模型：

3. Can we only focus on Critical Parts?

之前我们讲的是人工的方式告诉你哪些部分的 attention 也许不用计算了，但这种方式并不一定是最好的，因此想能不能变成以 data driven 的方式来寻找哪些不用计算了。

一个 Attention Matrix 可能如下所示：

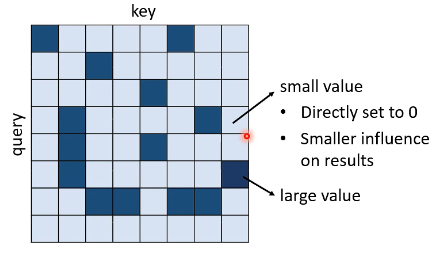
会有一部分的 attention weight 是很小的，如果把这些 small value 直接设为 0，对结果的影响也是很小的，却能加快计算。因此现在的问题是：How to quickly estimate the portion with small attention weights?

3.1 Clustering

这一技术在 Reformer (opens new window) 和 Routing Transformer (opens new window) 都有运用。

Step 1

对 query vector 和 key vector 基于 similarity 做 clustering，分成几种不同类型的 vector。下图示例是分成了 4 种 vector：

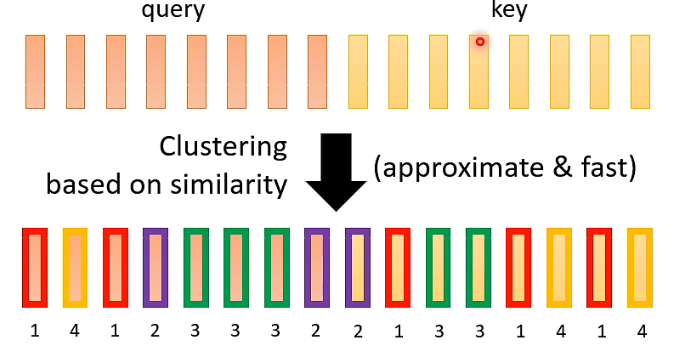
• 上图中，相同颜色边框的 vector 是同一类的 vector。

也许你会怀疑做 clustering 本身的计算量会不会有影响。如果 clustering 的计算复杂度达到了 sequence n 的 ，那确实没必要做这一步了，但实际上 clustering 有很多可以加速的方法，比如可以采用一个估测（approximate）的方法来进行 clustering。

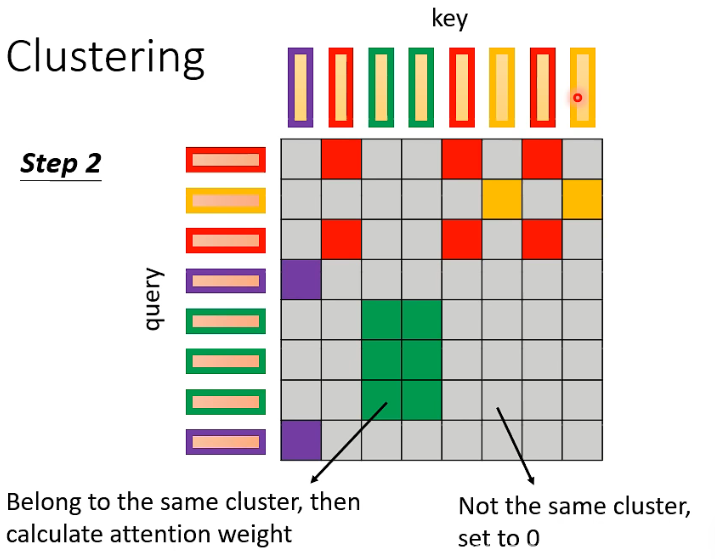
Step 2

相同 cluster 之间的 vector 计算 attention weight，其余的直接补 0：

到目前为止，所讲的方法还都是基于人类对这个问题的理解来决定要不要计算 attention weight，那有没有办法把“要不要计算 attention”这件事情用 learn 的方式直接把它学出来呢？这是有可能的。

3.2 Learnable Pattern - Sinkhorn Sorting Network

Sinkhorn Sorting Network 要做的就是“哪些地方要不要计算 attention 是直接通过 learn 的方式来得到“。

首先需要产生一个由 0/1 组成的 Matrix，值为 1 的位置才需要去计算 attention，如下图中深色部分代表 1：

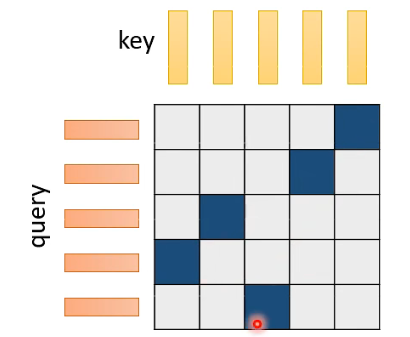
而这个 Matrix 怎么来的呢？而是需要 learn 另一个 network。input sequence 的每一个 vector 通过一个 neural network 产生另一个 vector，这个新产生的 vector 的长度需要与 sequence 一样，这样产生的一排 vector 就是 了：

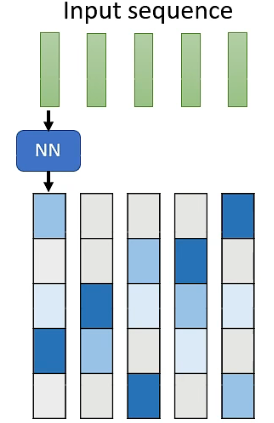
但这个新产生的一排 vector 构成的 matrix 的值是 continues 的，而我们一开始想要的 matrix 是 binary 的，所以我们需要做的就是把这个 continues 的 matrix 转成 binary 的 matrix，而这一步也是这个 model 的核心工作，具体怎么运作可以参考相关的文献 (opens new window)。

3.3 Do we need full attention matrix?

Linformer (opens new window) 的作者发现，完整的 attention martrix 大部分都是 low rank 的，从这个角度讲就是它包含很多 redundant columns，所以我们根本就不需要一个 的 matrix，那我们能不能把其中 redundant columns 去掉，从而产生一个比较小的 attention matrix，从而加快运算速度：

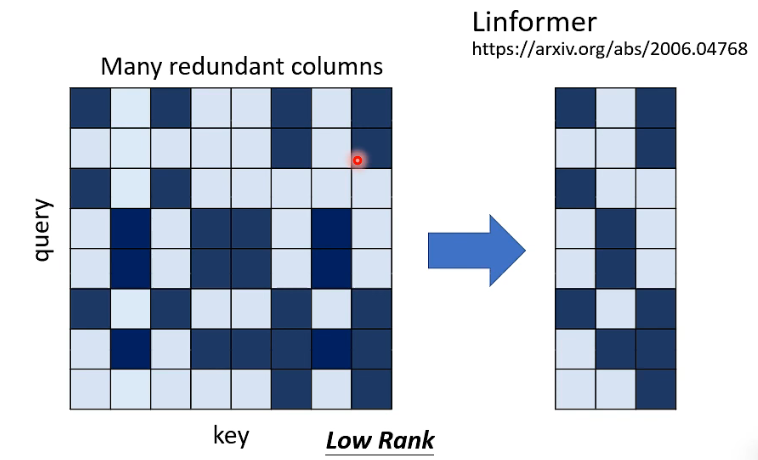
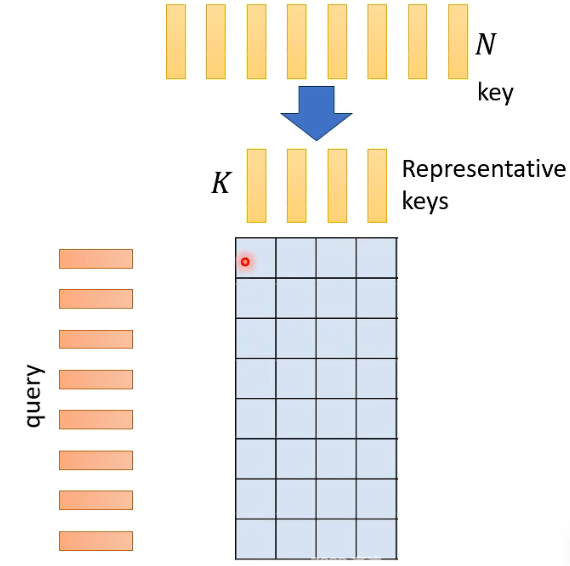
实际上的做法就是从 N 个 key 里面选出最具代表性的 K 个 key 用于计算 attention matrix，这样就不需要算一个完整的 attention matrix 了：

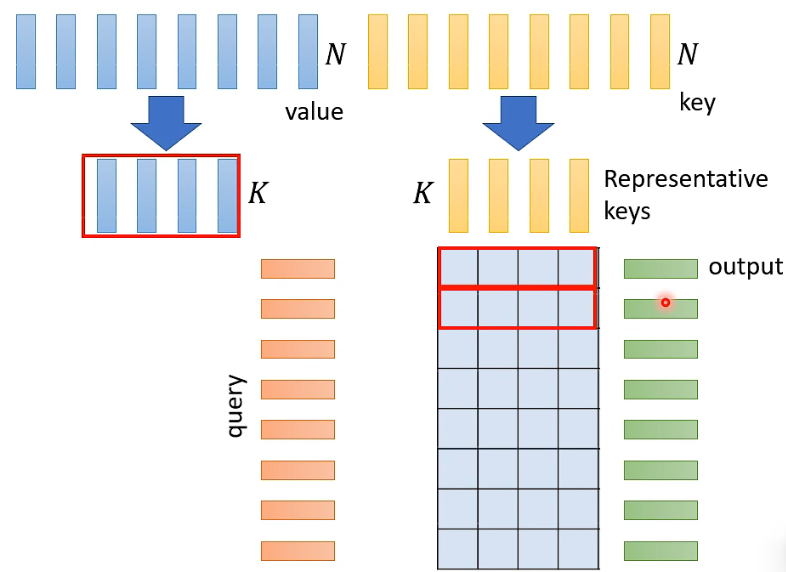
那怎样用这个 attention matrix 来产生 Attention Layer 的 output 呢？选出的 K 个 key 也具有与之对应的 K 个 value，然后就可以每 K 个 attention weights 与 K 的 value 做 weighted sum 得到一个 output vector：

到这里，你也许有个疑问：为什么是选 K 个有代表性的 key，而不是 query 呢？我们可以减少 query 的数量吗？我们注意，output 的 length 是与 query 的数量一致的，如果 query 减少的话，ouput sequence 也会相应减小。这种减小会有影响吗？这要看具体任务，比如 test classification，看完一遍 sequence 只需产生一个 label，那这时真的可以让 query 也变少，但假如具体任务是每一个 sequence 的位置都需要产生一个 label，那这时就有问题了，也就不能减少 query 的数量了。

下面讲怎么选有代表性的 key？一篇叫做 Compressed Attention 的 paper 的做法是用 CNN 来扫过 input sequence 从而使其变短，从而作为有代表性的 key。另外一个 Linformer 是把 N 个 key 拼成一个 的 matrix，然后让他去乘一个 的 matrix，从而得到一个 的 matrix，这个得到的矩阵的每一个 column 都是一个有代表性的 key。如下图所示：

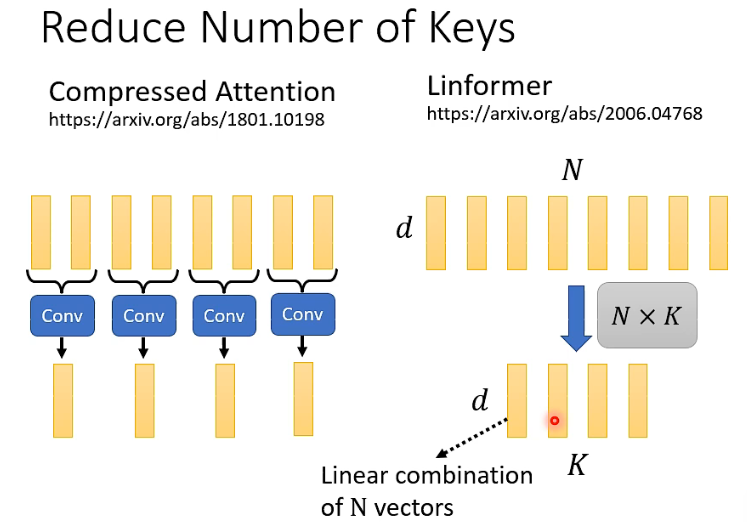
• Linformer 中我们可以看到，其实选出来的每一个有代表的 key 都是以前 N 个 key vector 的 linear combination。

4. 从矩阵运算的角度考虑简化

其实 Attention Mechianism 就是 three-matrix multiplication，我们先来复习一下这个运算过程：

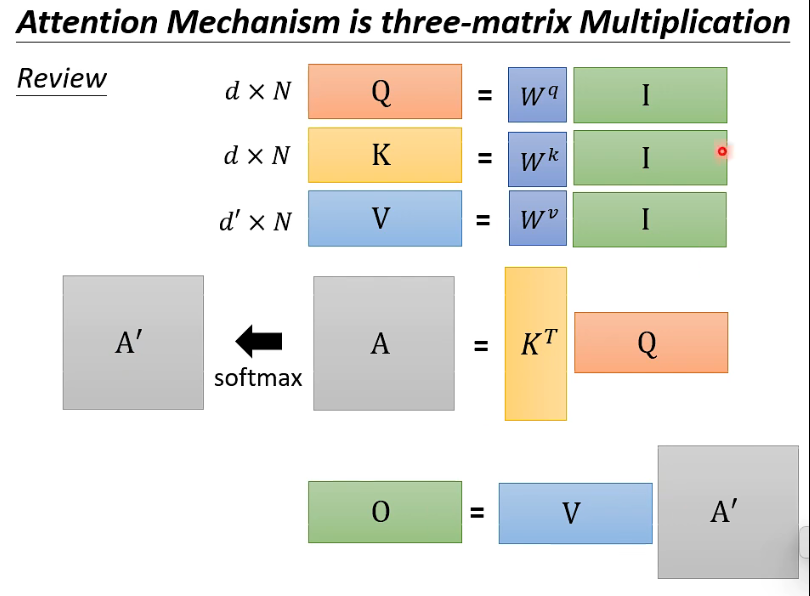
• 注意这里 V 矩阵的 size 是可以与 Q、K 的不一样的，大部分情况下我们是让 ，但其实也是可以不相等的。

现在我们先做一个假设，也就是没有从 的 softmax 这件事情，那么 self-aAttention 这件事情真正所做的就是下面这个过程：

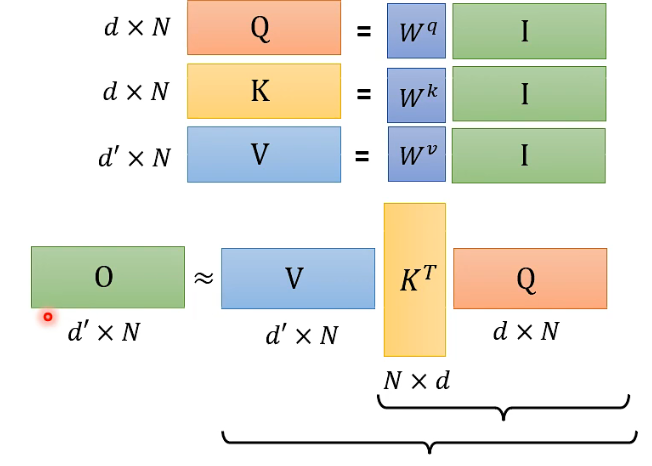
这个过程其实是可以加速的：

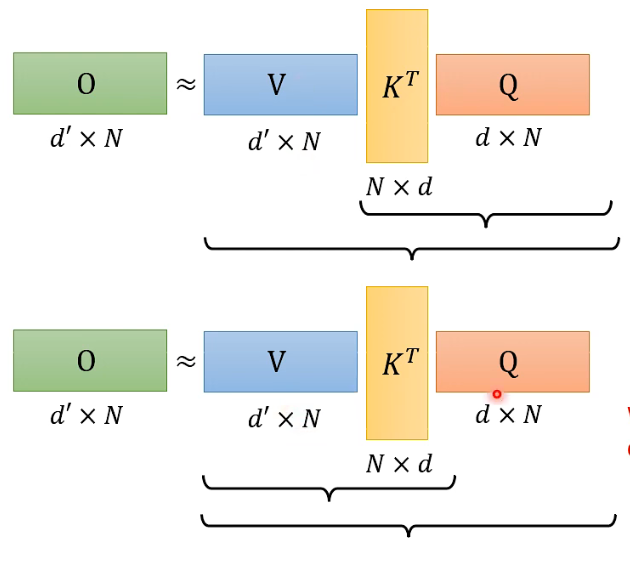
在上图中，上下两种结合方式的计算结果 是相同的，但计算复杂度却是不一样的。前者的计算次数是 ，而后者是 ，实际情况下 N 往往远大于 d，因此前者的复杂度是大于后者的。

刚刚是假设先忽略掉 softmax 过程，那把 softmax 拿回来会不会有影响呢？// TODO：数学很复杂，可以看李宏毅原视频，这里也涉及到多篇 paper。

5. Do we need q and k to compute attention?

做 self-attention，就一定需要用 q 和 k 去计算出 attention weights 吗？不一定，可以参考一种做法：Synthesizer!

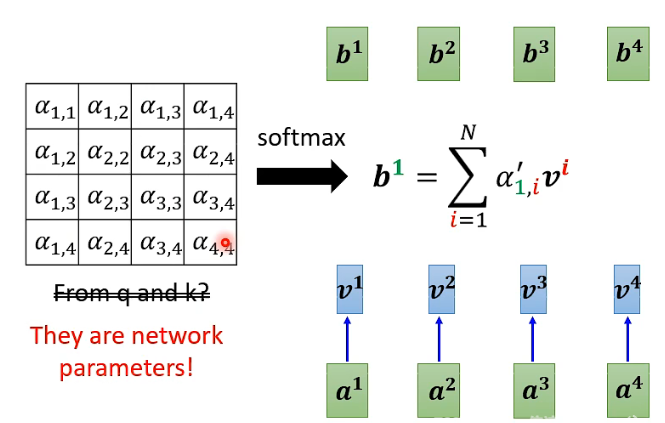
这里的 Attention Matrix 里有 个数值，这些数值不再是来自于 q 和 k，而是它们本身就是 network 的 paramters。这样再做 self-attention 时就不需要去计算 attention weights 了，因为它们本身就成为了参数的一部分了。

但有人可能会问，这样做的话对于不同的 input sequence，它们的 attention weights 都成一样的了，这样 performance 会变差吗？不会！就这样。所以这个 Synthesizer 让我们重新思考到底 attention 的价值到底是什么。

更进一步，人们开始思考处理 sequence 一定要用 attention 吗，于是开始寻找有没有可能丢掉 attention，去寻找 attention-free 的方法，所以有一系列的 paper 直接用 MLP 来处理 sequence：

• Fnet: Mixing tokens with fourier transforms (opens new window)
• Pay Attention to MLPs (opens new window)
• MLP-Mixer: An all-MLP Architecture for Vision (opens new window)

6. Summary

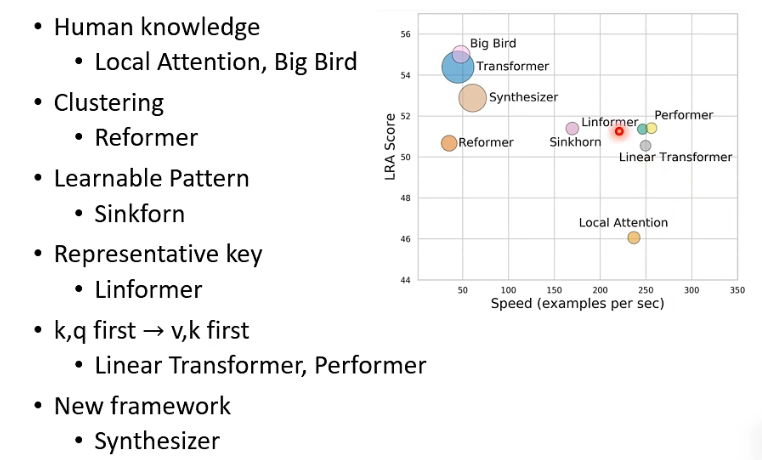
• 上面的坐标图是在一个 self-attention benchmark 上的结果，越往右表示速度越快，越往上表示 score 越好，即 performance 越好，圆圈大小代表运算所用 memory 大小，越大的圆圈代表所用越大的 memory。