 主成分分析(PCA)
主成分分析(PCA)
主成分分析(PCA)是一种数据压缩的算法,他将数据压缩到 K 维度,并使得所有数据投影到新维度的距离最小。
本章学习第二种类型的无监督学习问题,称为 Dimensionality Reduction(降维)。主成分分析(PCA)是一种数据压缩的算法,他将数据压缩到 K 维度,并使得所有数据投影到新维度的距离最小。
# 1. Motivation
# 1.1 Motivation 1:Data Compression
什么是 Dimensionality Reduction?用一个例子来解释,我们收集的数据集有两个 feature:
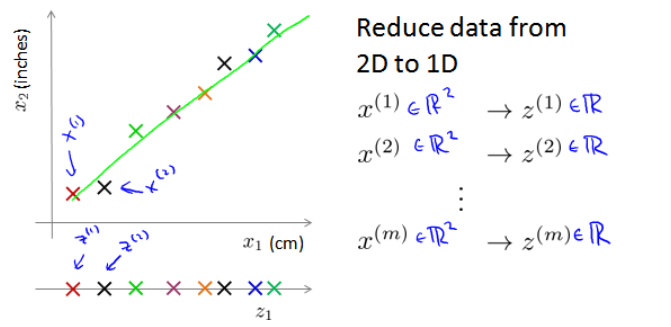
图中由于 inches 和 cm 两个单位在度量同一物体时出于四舍五入的精度问题,导致可能不完全是线性的。我们希望通过 Dimensionality Reduction,将原来 2D 的
从这件事情我看到的东西发生在工业上的事:有时可能有几个不同的工程团队,也许一个工程队给你二百个特征,第二工程队给你另外三百个的特征,第三工程队给你五百个特征,一千多个特征都在一起来描述一个 object 时,很有可能存在一些特征是高度冗余的。
我们再看一个将 3D 的 feature vector 降至 2D feature vector 的例子:
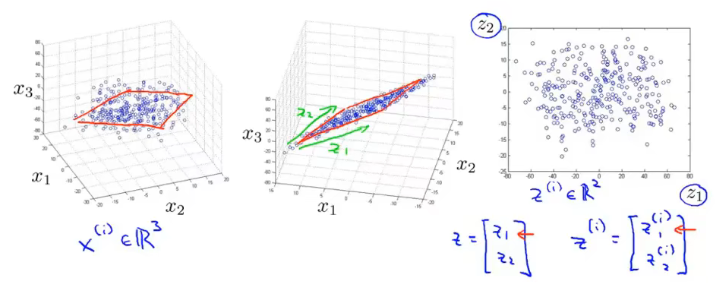
在最左边的图中,这些样本点虽然处于三维空间中,但实际上大部分都处于一个平面,因此可以进行降维。
这样的处理过程可以被用于把任何维度的数据降到任何想要的维度,例如将 1000 维的特征降至 100 维。
# 1.2 Motivation 2:Visualization
在许多机器学习问题中,如果我们能将数据可视化,我们便能寻找到一个更好的解决方案,降维可以帮助我们。
假使我们有有关于许多不同国家的数据,每一个特征向量都有 50 个特征(如 GDP,人均 GDP,平均寿命等)。如果要将这个 50 维的数据可视化是不可能的。使用降维的方法将其降至2维,我们便可以将其可视化了:
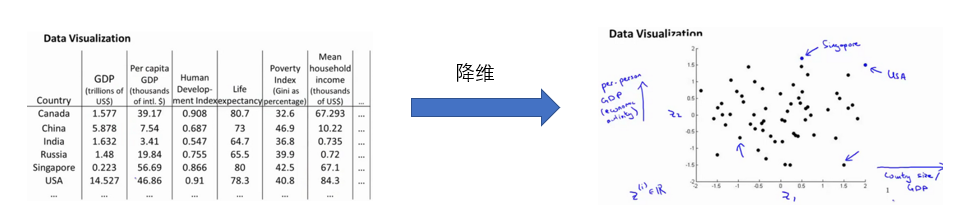
这样做的问题在于,降维的算法只负责减少维数,新产生的特征的意义就必须由我们自己去发现了。
# 2. PCA Problem
# 2.1 PCA Problem Formulation
主成分分析(PCA)是最常见的降维算法。
PCA 中,我们要做的是找到一个方向向量(Vector direction),当我们把所有的数据都投射到该向量上时,我们希望投射误差的平方和能尽可能地小:
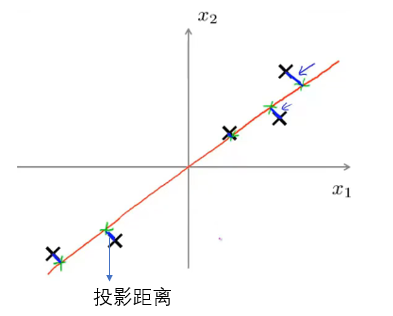
- 方向向量是一个经过原点的 vector。
- 投射误差(Projected Error)也就是投影距离,是从样本点向该方向向量作垂线的长度。
下面给出主成分分析问题的描述:
问题是要将 n 维数据降至 k 维;目标是找到 vectors

# 2.2 PCA v.s. Linear Regression
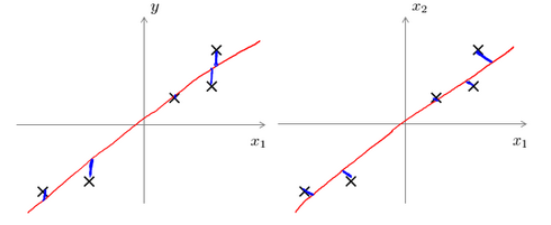
- Linear Regression 的目的是预测结果,而 PCA 不做任何预测
- 左边的是线性回归的误差(垂直于横轴投影),右边则是主要成分分析的误差(垂直于红线投影)
# 2.3 优点与缺点
PCA 技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
PCA 技术的一个很大的优点是,它是完全无参数限制的。在 PCA 的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。但是,这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
# 3. PCA Algorithm
PCA 将数据从 n 维减到 k 维:
PCA Algorithm
Reduce
Training set:
👣 Preprocessing【feature scaling / mean normalization】:
- Replace each
- If different features on different scales (e.g.
👣 Compute "covariance matrix"
👣 Compute “eigenvectors” of matrix
- 只取上面结果的
👣 写出
👣 计算
如果将每个
作为一行,堆积起来写作 ,那么协方差矩阵 又可以写成:
# 4. Reconstruction from Compressed Representation
我们使用 PCA 可以把 1000D features 的数据压缩到 100D features。如果这是一个压缩算法,应该能回到这个压缩表示,回到你原有的高维数据的一种近似。也就是说怎样从
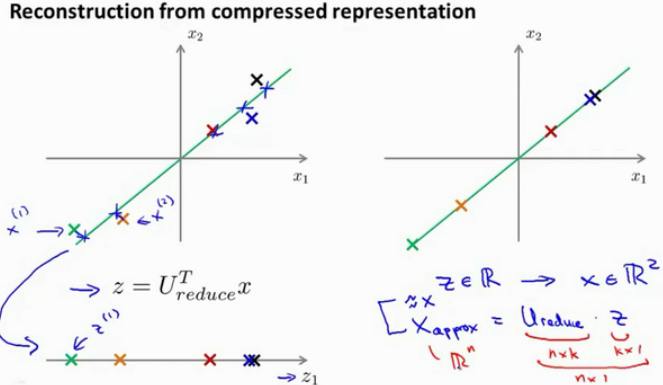
PCA Reconstruction
# 5. Choosing The Number Of Principal Components
PCA 将 n 维数据压缩到 k 维,但这个 k 怎么选呢?
PCA 的目的是减少 average squared projection error:
而 total variation in the data:
我们希望在 average squared projection error 与训练集 total variation 的比例尽可能小的情况下选择尽可能小的 k 值。如果我们希望这个比例小于1%,就意味着原本数据的 variation 有 99% 都保留下来了,如果我们选择保留 95% 的 variation,便能非常显著地降低模型中特征的维度了。
我们可以先令
还有一些更好的方式来选择 k。对 covariance matrix
# 6. Advice for Applying PCA
# 6.1 Supervised learning speedup
常常将 PCA 算法在 supervised learning 中用于加速:

注意:PCA 算法中计算
# 6.2 choose k
- Compression:
- Reduce memory/disk needed to store data
- Speed up learning algorithm
这时通过 variance retain 来选择 k。
- Visualization: k = 2 or k = 3
# 6.3 Bad use of PCA: To prevent overfitting
一些人认为:Use
也许这 OK,但不是一个好的方法去处理 overfitting,因为压缩过程是不考虑 label 信息的,这个压缩过程可能会丢失一些重要信息。往往使用 regularization 效果会更好。
# 6.4 不要滥用

在使用 PCA 之前,先尝试用原始数据
