1. 监督学习与无监督学习

• 监督学习是已经知道数据的 label，比如预测房价问题，给出了房子的面积和价格。
  • 回归问题是预测连续值的输出，例如预测房价。
  • 分类问题是预测离散值输出，例如判断肿瘤是良性还是恶性。
• 无监督学习是没有数据的 label，比如对于分类问题无监督学习可以得到多个不同的聚类，从而实现预测的功能。

2. 代价函数

之后的课程对符号做如下约定：

• 表示训练样本的数目
• 表示特征/输入变量
• 代表目标变量/输出变量
• 代表训练集中的实例
• 代表第 个观察实例
• 代表学习算法的解决方案或函数，也称为假设（hypothesis）

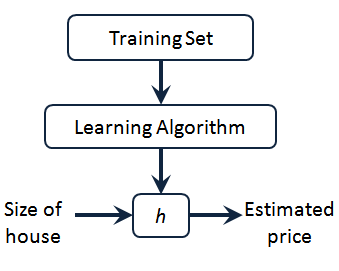
上图是一个监督学习算法的工作方式，把训练集喂给学习算法后输出一个函数，通常表示用 来表示， 代表 hypothesis（假设），它是一个函数，输入是房屋尺寸大小（），输出是预测的价格（）。

也许 hypothesis 这个名字不是很合适，但一开始就是这么叫的，所以也就流传下来了。

对于我们的房价预测问题，该如何表达 呢？一种可能的表达方式为：，因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题。

2.1 什么是 cost function？

在线性回归中我们有一个像这样的训练集，训练样本数量 m=47，而我们的 hypothesis function 形式是这样：。接下来我们要做的是为模型选择合适的 parameters ，在这个例子中就是直线的斜率 和 y 轴上的截距 。

我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）。

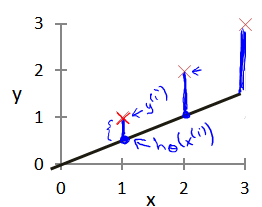
我们的目标便是选择出可以使得建模误差能够最小的模型参数，也就是使得代价函数 最小化，可以写作 ，其中 ，它也是 square error function。

我们绘制一个等高线图，三个坐标分别是 、 和 ：

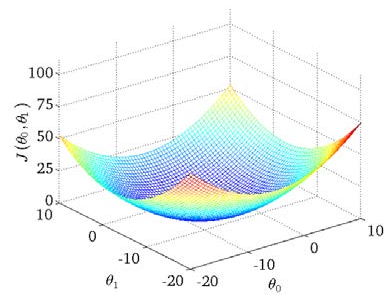
在一个固定数据集 中，每一个 parameter 确定一个 hypothesis function ，进而确定了一个 cost function ，上图中的点是在这个数据集 上通过函数 计算出来的一个 error value。

为什么叫代价函数？当 model 的预测值与实际 label 的差距较大时，该函数的值也应当较大，即应该付出一个较大的代价来惩罚 model；相反两者差距较小时，付出的代价也就较小。

2.2 cost function 的直观理解

将上面三维空间的图画成等高线图可以表示为：

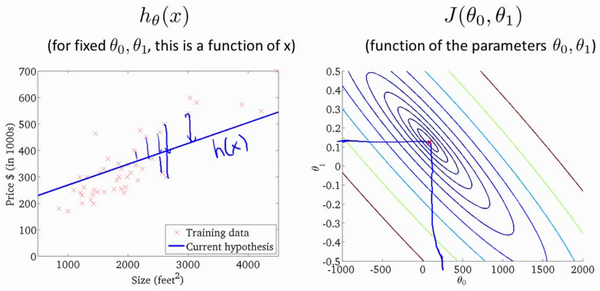
我们真正需要的是一种有效的算法，能够自动地找出这些使代价函数 取最小值的参数 和 来。

3. 梯度下降

3.1 批量梯度下降

• 表示学习率

我们使用 := 表示 Assignment，= 表示 Assert Truth。

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即：

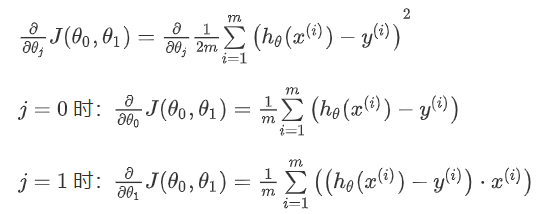
则算法改写成：

刚刚使用的算法称为批量梯度下降，指的是在梯度下降的每一步中，我们都用到了所有的训练样本。因此，批量梯度下降法这个名字说明了我们需要考虑所有这一"批"训练样本，而事实上，有时也有其他类型的梯度下降法，不是这种"批量"型的，不考虑整个的训练集，而是每次只关注训练集中的一些小的子集。

3.2 multi-feature 的梯度下降

我们对以下符号做出约定：

• ：feature 的数量
• ：代表第 i 个训练实例，是 feature matrix 的第 i 行，是一个 vector
• ：代表 feature matrix 的第 i 行的第 j 个特征，也就是第 i 个训练实例的第 j 个特征

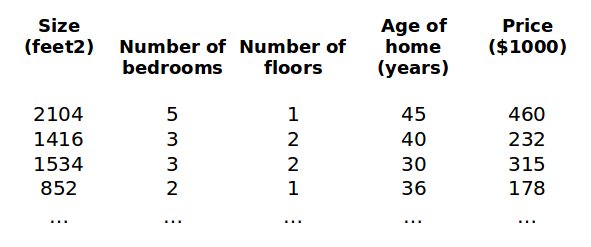
支持 multi-feature 的 hypothesis 可以表示为：，其中 。此时模型的参数是一个 n+1 维的 vector，任何一个训练实例也都是 n+1 维的 vector，feature matrix 的维度是 ，因此公式可以简化为：。

在多变量线性回归中，cost function 也可以写成 ，此时多变量线性回归的批量梯度下降算法为：

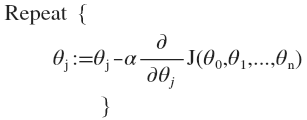
求导的步骤计算后即：

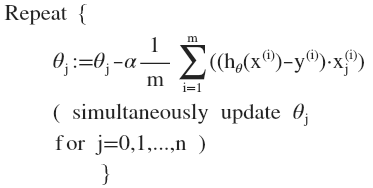
我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。

3.3 Feature Scaling

Idea: Make sure features are on a similar scale.

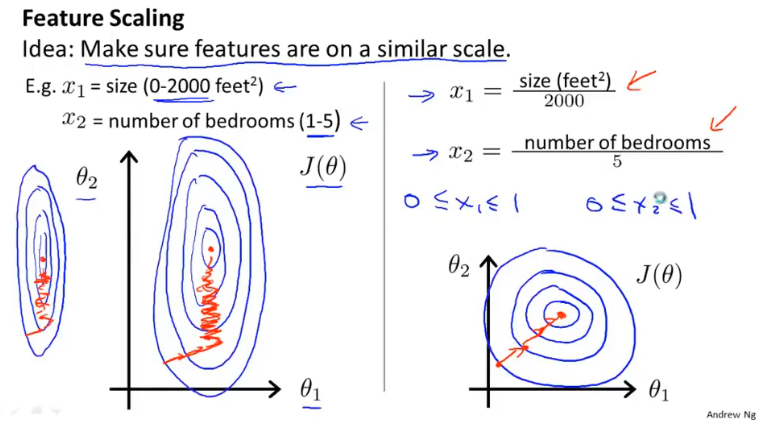
最简单的方法是令 ，其中 是平均值， 是标准差。

3.4 Learning Rate

• If is too small: slow convergence.
• If is too large: may not decrease on every iteration; may not converge.

To choose , try