 Logistic Regression
Logistic Regression
# 1. Classification Problem
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。我们从二元的分类问题开始讨论。
我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则 dependent var
为什么不能用 Linear Regression 的 hypothesis 来解 classification 问题?对于 classification,y range from 0 or 1,但如果使用 Linear Regression,那 hypothesis func 的 output 可能远大于 1 或 远小于 0,而 label 取值 0 或 1,这样就会感觉很奇怪。因此我们需要研究 Logistic Regression,其 output 永远在 0~1 之间,它适用于 label y 取值离散的情况,比如 0 1 1 0。
Logistic Regression 是一个 classification 算法,不要被名字里面的 “regression” 给迷惑了。
# 2. Hypothesis Representation
本节展示 logistic regression 的 hypothesis func 表达式。我们希望它的值在 0 和 1 之间,此时就有了:
- 当
- 当
Logistic Regression 模型的 hypothesis 是:
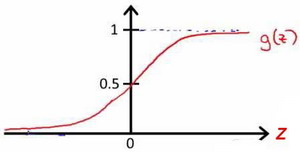
其中 X 代表特征向量,g 代表 logistic function,它也是 sigmoid function,公式为
# 3. Decision Boundary
在 Logistic Regression 中,我们预测:
- 当
- 当
根据 logistic function 的 S 型函数图像,我们知道:
- z = 0 时 g(z) = 0.5
- z > 0 时 g(z) > 0.5
- z < 0 时 g(z) < 0.5
又
现在假设我们又有一个模型:
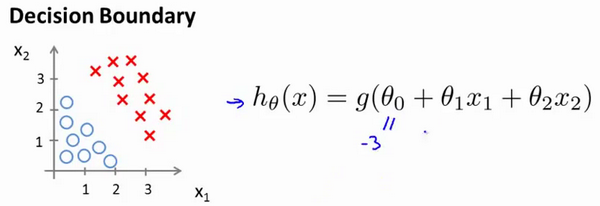
现在假设参数
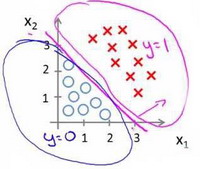
对于更复杂的数据分布情况,z 可能需要是二次方特征来划分出 Decision Boundary:
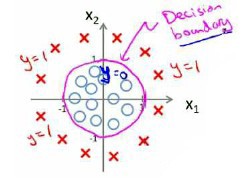
我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
# 4. Cost Function
本节介绍如何拟合 logistic regression 的 param

对于线性回归模型中,我们定义的代价函数是所有模型误差的平方和。理论上我们对 logistic regression 也可以沿用这个定义,但问题在于将 logistic regression 的
我们先看一下 logistic regression 的 loss function(error function),它可以用来衡量算法的运行情况:
- if y=1,
- if y=0,
loss function 是在单个 training example 上定义的,它衡量了你在单个 training example 上的表现。而 cost function 衡量的是在全体 training example 上的表现。这样我们可以定义 cost function
在得到这样一个 cost function 以后,我们便可以用 gradient descent 算法来求得能使 cost function 最小的 param 了。
To fit parameters

# 5. 将 logistic regression 用于多类别分类
本节主要谈如何使用 logistic regression 来解决多类别分类问题,具体来说是通过一个叫做“一对多”(one-vs-all)的分类算法。
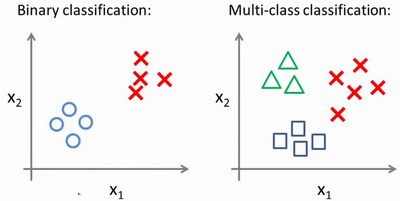
我用3种不同的符号来代表 3 个类别,问题就是给出3个类型的数据集,我们如何得到一个学习算法来进行分类呢?使用逻辑回归可以将数据集一分为二为正类和负类,而下面这个叫做“one-vs-all”或“one-vs-rest”的方法可用于多分类。
现在我们有一个训练集,好比上图表示的有 3 个类别。先从用三角形代表的类别 1 开始,我们可以创建一个新的"伪"训练集,类型 2 和类型 3 定为负类,类型 1 设定为正类,然后可以拟合出一个合适的分类器:
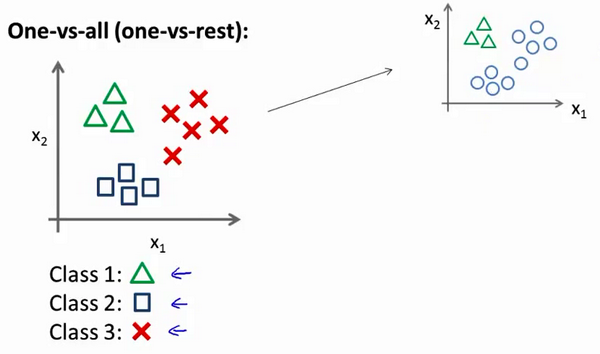
这里的三角形是正样本,而圆形代表负样本,这样可以训练一个标准的逻辑回归分类器,我们将这个 y=1 标为正向类而训练的 model 记作
在我们训练完这些分类器后,为了做出预测,给输入一个新的 x 值,我们要做的就是在我们三个分类器里面分别输入 x,然后我们选择一个让
通过这个小方法,现在也可以将逻辑回归分类器用在多类分类的问题上了。
