 Neural Network
Neural Network
# 1. Neural Network Layer
# 1.1 One layer
在一个 layer 中,发生如下的计算:
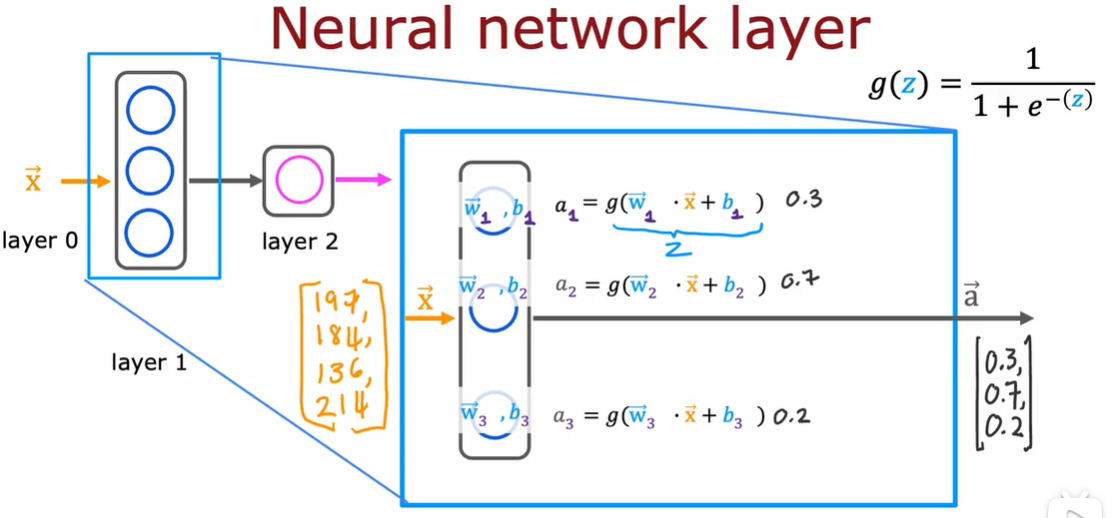
由于这是发生在 layer 1 中,因此也往往将这一层的 params [1],计算的结果是
在 layer 2 中,便会发生如下的计算:
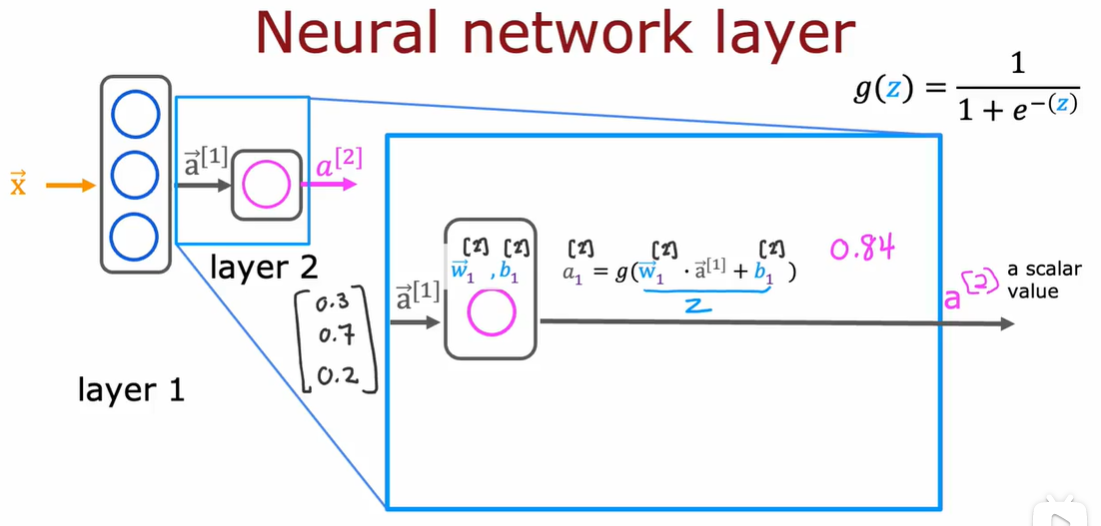
注意这里上标的含义。
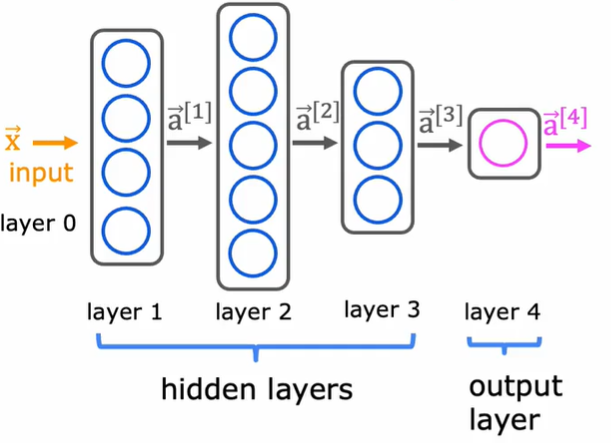
# 1.2 More complex neural network
将 layer 进行叠加可以得到:
# 2. Advice for Applying Machine Learning
# 2.1 Evaluating a Hypothesis
当我们确定学习算法的 params 的时候,我们考虑的是选择 params 来使训练误差最小化。但仅仅是因为这个 hypothesis 具有很小的训练误差,并不能说明它就一定是一个好的 hypothesis function,因为可能出现 overfitting。那么该如何判断一个 hypothesis func 是否 overfitting 呢?
按照经验可以将数据按照 7:3 分成 training set 和 test set。很重要的一点是 training set 和 test set 均要含有各种类型的数据,通常我们要对数据进行“洗牌”,然后再划分。
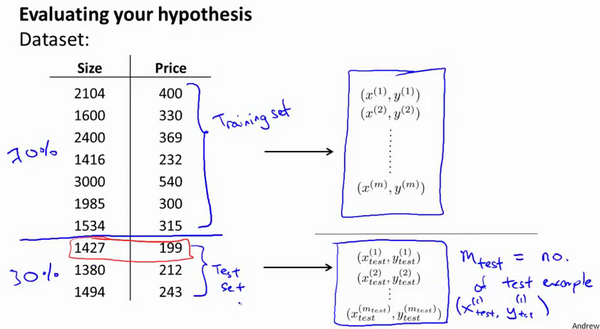
在通过 training set 让我们的 model 学习得出其 params 后,对 test set 运用该模型通过计算代价函数
# 2.2 Model Selection and Train-Validation-Test
在有了 testing set 后,我们可以首先用 training set 得到一个最优的参数
但这样做并不能评估模型的泛化能力,通过 testing set 评估选择的模型,可能刚好适合 testing set 的数据,并不能说明它对其他数据的预测能力,这时就引入了 validation set。
因此我们可以将数据分成:training set、validation set 和 testing set。
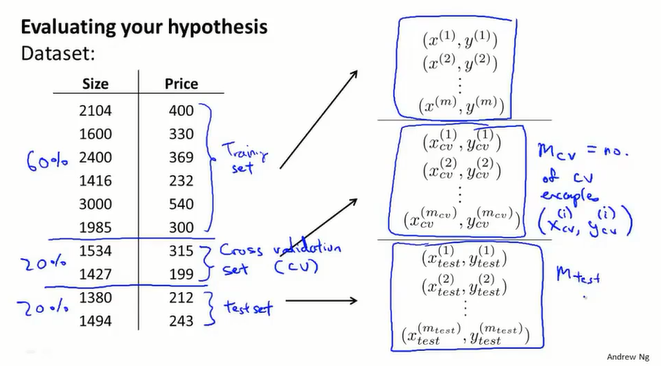
验证集也称为 Cross Validation Set(CV),但往往称之为 validation set。
对于每个集合都可以计算相应的误差:

这样在选择模型的时候,可以先使用 training set 得到每个模型的
# 2.3 Bias and Variance
当运行一个算法时,如果一个算法表现不理想,那么多半是出现了两种情况:要么是 high bias,要么是 high variance。

- 在 Bias (underfit) 的情况下,
- 在 Variance (overfit) 的情况下,
# 2.4 Regularization and Bias_Variance
在我们在训练模型的过程中,一般会使用一些正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了,即我们在选择
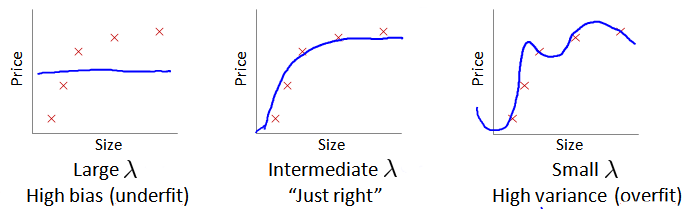
怎样去选择正则化参数

- 选取一系列的
- 对每个候选值,通过 training set 训练出一个
将每个

# 2.5 Learning Curve
学习曲线(Learning Curve)是用来判断某一个学习算法是否处于偏差、方差问题的很好的工具。学习曲线是将 training set 误差和 validation set 误差作为 training set 样本数量(m)的函数绘制的图表。
随着数据量的增加,
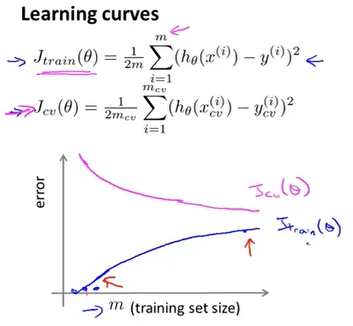
# 1)high bias model 的 learning curve

- 因为参数很少,数据很多,所以随着数据的增多高偏差的模型的
θ
# 2)high variance model 的 learning curve

- high variance 的特点是 training set 和 validation set 之间有很大的差距,这时可以选择增加数据,随着图像右移可以看出训练误差和验证误差会慢慢接近。
# 2.6 决定接下来做什么
Suppose you have implemented regularized linear regression to predict housing prices. However, when you test your hypothesis in a new set of houses, you find that it makes unacceptably large errors in its prediction. What should you try next?
- Get more training examples. –> fix high variance
- Try smaller sets of features –> fix high variance
- Try getting additional features –> fix high bias
- Try adding polynomial features –> fix high bias
- Try decreasing
- Try increasing
# 3. Machine Learning System Design
# 3.1 首先要做什么
这一章将谈及在设计复杂的机器学习系统时,你将遇到的主要问题。同时我们会试着给出一些关于如何巧妙构建一个复杂的机器学习系统的建议。
以一个垃圾邮件分类器算法为例进行讨论。 为了解决这样一个问题,我们首先要做的决定是如何选择并表达特征向量
为了构建这个分类器算法,我们可以做很多事,例如:
- 收集更多的数据,让我们有更多的垃圾邮件和非垃圾邮件的样本
- 基于邮件的路由信息开发一系列复杂的特征
- 基于邮件的正文信息开发一系列复杂的特征,包括考虑截词的处理
- 为探测刻意的拼写错误(把 watch 写成 w4tch)开发复杂的算法
在上面这些选项中,非常难决定应该在哪一项上花费时间和精力。当我们使用机器学习时,总是可以“头脑风暴”一下,想出一堆方法来试试。接下来讲的误差分析,会告诉你怎样用一个更加系统性的方法,从一堆不同的方法中,选取合适的那一个。
# 3.2 误差分析(Error Analysis)
误差分析会帮助你更系统地做出决定应该做什么事。如果你准备研究机器学习的东西,或者构造机器学习应用程序,最好的实践方法不是建立一个非常复杂的系统,拥有多么复杂的变量,而是构建一个简单的算法,这样你可以很快地实现它。每当我(吴恩达)研究机器学习的问题时,我最多只会花一天的时间,就是字面意义上的24小时,来试图很快的把结果搞出来,即便效果不好。坦白的说,就是根本没有用复杂的系统,但是只是很快的得到的结果。即便运行得不完美,但是也把它运行一遍,最后通过交叉验证来检验数据。一旦做完,你可以画出学习曲线,通过画出学习曲线,以及检验误差,来找出你的算法是否有高偏差和高方差的问题,或者别的问题。在这样分析之后,再来决定用更多的数据训练,或者加入更多的特征变量是否有用。
这么做的原因是:这在你刚接触机器学习问题时是一个很好的方法,你并不能提前知道你是否需要复杂的特征变量,或者你是否需要更多的数据,还是别的什么。因此,你很难知道你应该把时间花在什么地方来提高算法的表现。但是当你实践一个非常简单即便不完美的方法时,你可以通过画出学习曲线来做出进一步的选择。除了画出学习曲线之外,一件非常有用的事是误差分析,我的意思是说:当我们在构造垃圾邮件分类器时,我会看一看我的交叉验证数据集,然后亲自看一看哪些邮件被算法错误地分类。因此,通过这些被算法错误分类的垃圾邮件与非垃圾邮件,你可以发现某些系统性的规律:什么类型的邮件总是被错误分类。经常地这样做之后,这个过程能启发你构造新的特征变量,或者告诉你:现在这个系统的短处,然后启发你如何去提高它。
构建一个学习算法的推荐方法为:
- 从一个简单的能快速实现的算法开始,实现该算法并用交叉验证集数据测试这个算法
- 绘制学习曲线,决定是增加更多数据,或者添加更多特征,还是其他选择
- 进行误差分析:人工检查交叉验证集中我们算法中产生预测误差的样本,看看这些样本是否有某种系统化的趋势
在分析过程中,最好有一个可以量化的数值评估,你可以看看这个数字,误差是变大还是变小了。你可以通过它更快地实践你的新想法,它基本上非常直观地告诉你:你的想法是提高了算法表现,还是让它变得更坏,这会大大提高你实践算法时的速度。
假设你有了一个快速而不完美的算法实现,又有一个数值的评估数据,这会帮助你尝试新的想法,快速地发现你尝试的这些想法是否能够提高算法的表现,从而你会更快地做出决定,在算法中放弃什么,吸收什么误差分析可以帮助我们系统化地选择该做什么。
# 3.3 类偏斜的误差度量
我们之前说了设定误差度量值的重要性,也就是说设定某个实数来评估你的学习算法,并衡量它的表现。有一件重要的事情要注意,就是使用一个合适的误差度量值,这有时会对于你的学习算法造成非常微妙的影响,这件重要的事情就是偏斜类(skewed classes)的问题。
类偏斜情况表现为我们的训练集中有非常多的同一种类的样本,只有很少或没有其他类的样本。 例如我们希望用算法来预测癌症是否是恶性的,在我们的训练集中,只有0.5%的实例是恶性肿瘤。假设我们编写一个非学习而来的算法,在所有情况下都预测肿瘤是良性的,那么误差只有0.5%。然而我们通过训练而得到的神经网络算法却有1%的误差。这时,误差的大小是不能视为评判算法效果的依据的。
在分类问题中,将机器学习模型的预测与实际情况进行对比后,结果可以分为四种:TP、TN、FN 和 FP。具体来说,也就是:
| 全称 | 预测结果 | 事实 | |
|---|---|---|---|
| TP | True Positive,真阳性 | 正类 | 正类 |
| TN | True Negative,真阴性 | 负类 | 负类 |
| FP | False Positive,假阳性 | 正类 | 负类 |
| FN | False Negative,假阴性 | 负类 | 正类 |
这与检测新冠时的说法一样。比如 False Positive “假阳性”,指的是检测出阳性但实际本人为阴性。
# 1)Precision 精确率
- 指的是检测阳性中有多少是真的阳性。
- “不可滥杀无”
# 2)Recall 召回率
- 指的是有多少比例的阳性被检测出来了。
- “宁可杀错一千也不放过一个”
# 3)Accuracy 准确率
- 指的是模型猜对了的结果在全部结果中的占比。
# 3.4 precision 与 recall 之间的权衡
在很多应用中,我们希望能够保证查准率和召回率的相对平衡。继续沿用刚才预测肿瘤性质的例子。假使,我们的算法输出的结果在 0-1 之间,我们使用阀值 0.5 来预测真和假:

如果我们希望只在非常确信的情况下预测为真(肿瘤为恶性),即我们希望更高的 precision,我们可以使用比 0.5 更大的阀值,如 0.7,0.9。这样做我们会减少错误预测病人为恶性肿瘤的情况,同时却会增加未能成功预测肿瘤为恶性的情况。如果我们希望提高 recall,尽可能地让所有有可能是恶性肿瘤的病人都得到进一步地检查、诊断,我们可以使用比 0.5 更小的阀值,如 0.3。我们可以将不同阀值情况下,查全率与查准率的关系绘制成图表,曲线的形状根据数据的不同而不同:
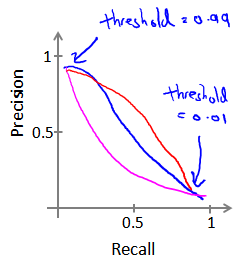
如何权衡这两个值呢?

- 如果选取 precision 与 recall 的 average,可以看到 Algorithm 3 的 average 最小,但此时的 recall == 1,显然不是一个好的 model,因此不能选用 average 作为指标。
- 应该选用
选用 F Score 的话,极端情况为:
- when P=0 or R=0 => F Score=0;
- when P=1 or R=1 => F Score=1;
这也是符合我们所期望的。正常情况下 F Score 都会介于 0~1 之间。
F Score 权衡了 precision 和 recall,可以作为度量值(evaluation metric)。当然也可以去尝试一系列的 threshold 来选择用哪个。
# 3.5 机器学习的数据
用于训练的数据的关键所在是:
- 一个人类专家看到了特征值 x,能否有信心预测出 y 值?比如只根据房子大小,即使是一个房地产专家也不太可能能预测出其价格。
- 是否能得到足够的训练集,并且在这个训练集上训练一个有很多参数的 model?
