1. overfitting 问题

当我们将算法应用到特定的任务时，可能会遇到 overfitting 的问题使得效果变差。这一节将解释什么是 overfitting 问题，并在之后的几节讨论 regularization 的技术来改善或减少 overfitting 问题。

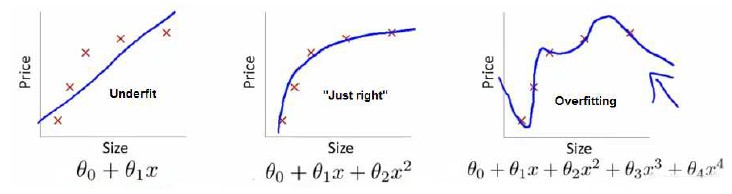
第一张图片是 undefit，具有 “high bias”，第三张图片是 overfitting，具有“high variance”。

Options of addressing overfitting：

1. Reduce number of features.
   • Manually select which features to keep.
   • Model selection algorithm(later in course).
2. Regularization
   • Keep all the features, but reduce magnitude/values of parameters .
   • Works well when we have a lot of features, each of which contributes a bit to predicting .

2. cost function

当我们介绍 regularization 是怎么运行时，我们还将写出相应的 cost function。

下图中可以看出，正是高次项导致了 overfitting 的产生，所以有一个想法：如果能让这些高次项的系数接近于 0 的话，我们就能很好地拟合了，所以我们要做的就是在一定程度上去减小这些参数 的值。这就是 regularization 的思想。

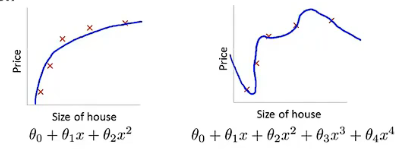
我们既然决定要修改 和 的大小，那我们要做的就是修改 cost function，在其中对 和 设置一点惩罚。修改后的 cost function 如下：

其中蓝色部分为惩罚项，1000 这个数只是表示很大的一个数。有了这两个惩罚项，训练的结果就会是 和 尽可能接近 0，最终得到一个类似于二次函数的一个拟合函数，并可以表现很好。

但假如我们有非常多的 feature ，同时有 parameters ，那我们并不知道其中要选哪些 params 去惩罚最好，这样我们就会对所有的 params 进行惩罚，并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的 hypothesis，cost func 如下：

其中蓝色部分是正则化项（regularization term）， 被称为正则化参数（regularization parameter）。这个 是用来控制两个不同目标之间的取舍，一个目标与 cost function 的第一项有关，就是想让 model 更好地拟合数据，第二个目标与 cost function 的第二项有关，就是想让 parameters 尽量地小。 就是控制了这两个目标之间的平衡关系，即更好地拟合训练集的目标和将 params 控制地更小的目标。

这里 model 一共有 parameters ，按照惯例只对 进行了惩罚，并不对 进行惩罚。但其实也可以对它惩罚，这影响不大，所以往往按照惯例的做法。

但如果 过大的话，会使得所有 （不包括 ）都趋于 0，从而我们只得到了一条平行于 x 轴的直线：，这就是一个 underfitting 的现象。所以我们需要选个一个合适的 regularization parameter ，才能更好地应用 regularization。

3. Regularized Linear Regression

正则化线性回归的代价函数为：

如果我们要使用梯度下降法令这个代价函数最小化，因为我们没有对 进行正则化，所以梯度下降算法将分成两种情形：

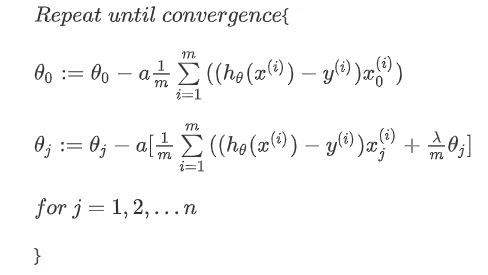
对上面的算法中的 时的更新式子进行调整可得：

上面式子中的 这一部分很有趣，，因此正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令 值减少了一个额外的值。