Creation. 一个模型能够判别猫和狗，但它不一定就真的了解猫和狗是什么，但如果有一天 machine 可以自己画出一只猫的时候，那它对于猫这个东西的概念或许就不一样了。

Generative Models：

• PixelRNN
• Variational Autoencoder（VAE）
• Generative Adversarial Network（GAN）

1. PixelRNN

想法：To create an image, generating a pixel each time. 比如对于一个 3 * 3 的 image，我们先随机给第一个 pixel，然后将这个 pixel 输入到一个已经学好的 model 中，然后会输出一个 pixel，这个 pixel 就作为 image 的第二个 pixel：

下一步也是类似这样，把前两个 pixel 输入到 NN 中，输出第三个 pixel：

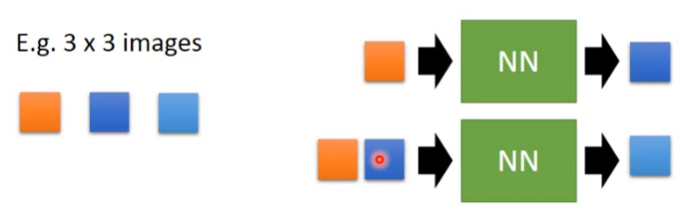
但这里为何在不同的时候可以输入不同数量的 pixel 呢？RNN 可以做到这一点。

这个 NN 怎么训练呢？Can be trained just with a large collection of images without any annotation.

这个方法竟然是 work 的，下面是一个例子：

这种其实也可以用在语音上，比如 WaveNet。原影片展示了这个模型的运作过程。

原影片这里还展示了绘制宝可梦图片的示例。

在做这种 generation 的 task，一个难点是：It is difficult to evaluate generation.

2. VAE

我们已经学习过了 Auto-Encoder，它是想让 input 与 output 尽可能接近，他把一个 image 输入给 Encoder 得到 code，再把这个 code 给 Decoder 得到输出的 image。但如果我们只把 Decoder 拿出来，并 randomly generate 一个 vector 作为 code 输给 Decoder，这样也许 Decoder 就可以输出一个 image：

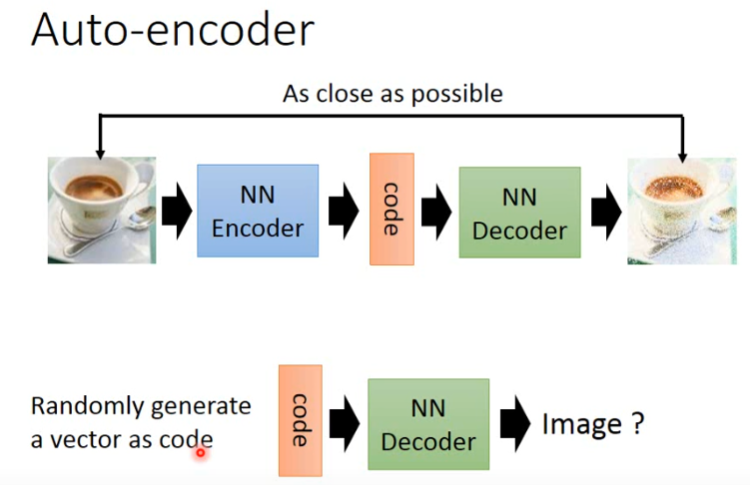
但这样做的话，通常 performance 不会很好。而应该用 VAE 才能得到好的结果。VAE 在 AE 的中间加了一点小 trick：

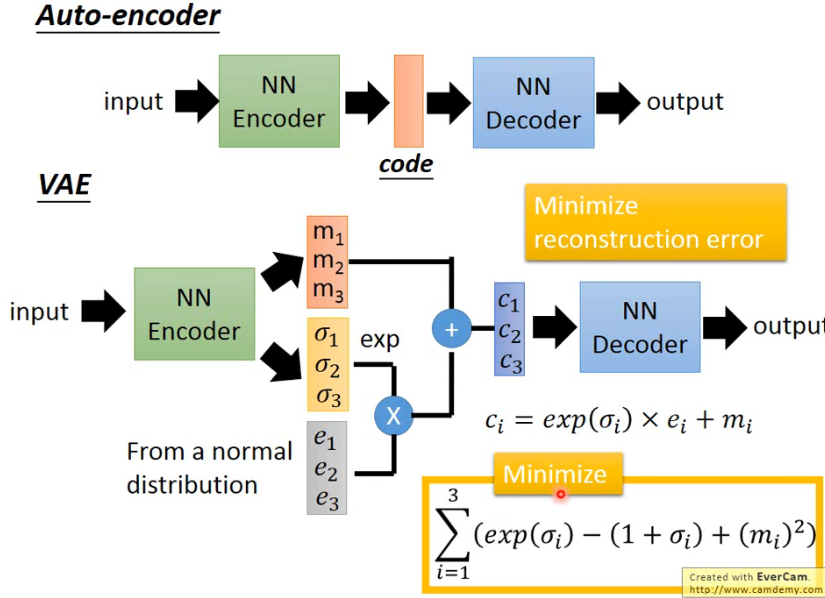
2.1 Why VAE?

先来看一个 intuitive reason：

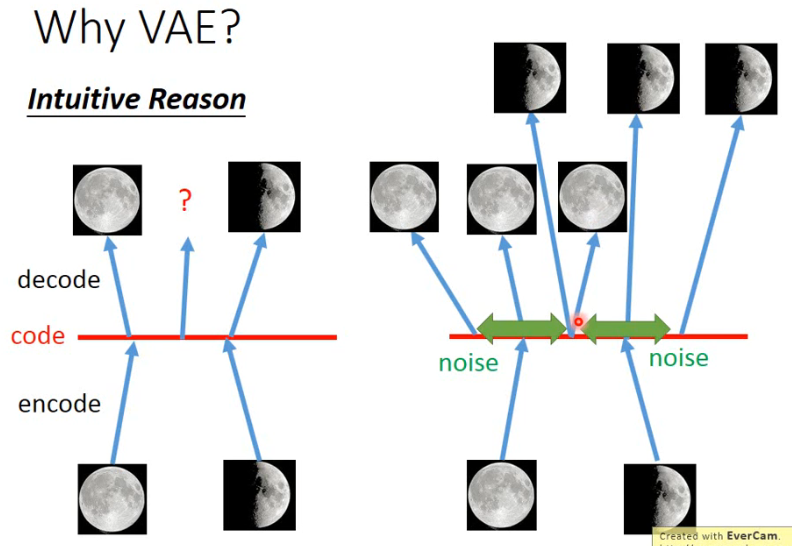
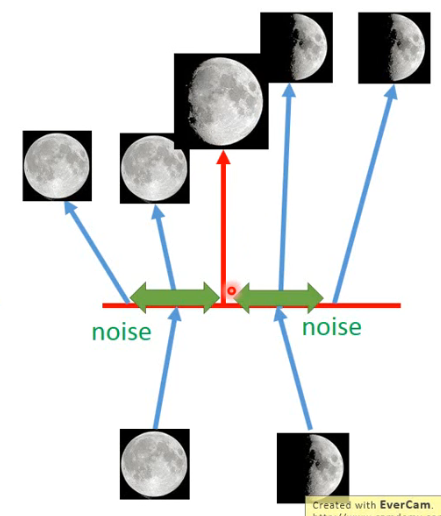
• 左边是一个 AE 的思路，我输入一个满月，经过 encode 得到 code，再由这个 code 还原为满月；然后再输入一个弦月，经过 encode 得到 code，再由这个 code 还原为弦月。但如果我拿中间的这个 code 用来还原，也许你期待能够得到一个介于满月和弦月之间的月亮，但由于 neural network 是 non-linear 的，所以其实很难预测说中间这个 code 到底会发生什么。
• 但如果用 VAE 有什么好处呢？如右图，当你把满月的 image 经过 encode 变成 code 时，会再在这个 code 上面加一个 noise，然后希望在加上 noise 以后，这个 code 经过 reconstruct 后还是一张满月的 image，也就是在那个范围以内都可以 reconstruct 为原来的图。另一个弦月的 image 也是这样，变成 code 再加上 noise 以后，这个范围内的 code 经过 reconstruct 都可以变回弦月的 image。这时你会发现说，中间位置的这个 code 会希望被 reconstruct 回弦月的图，同时也希望被 reconstruct 回满月的图。但这只能被 reconstruct 回一张图，VAE 在训练时是 minimize Mean Square Error，最后这个位置所产生的图就会是介于满月和弦月之间的一个图。那这样或许就会有下面这个效果，它产生了介于满月和弦月之间的图：

因此可以看到 VAE 的网络如下面这个图所示：

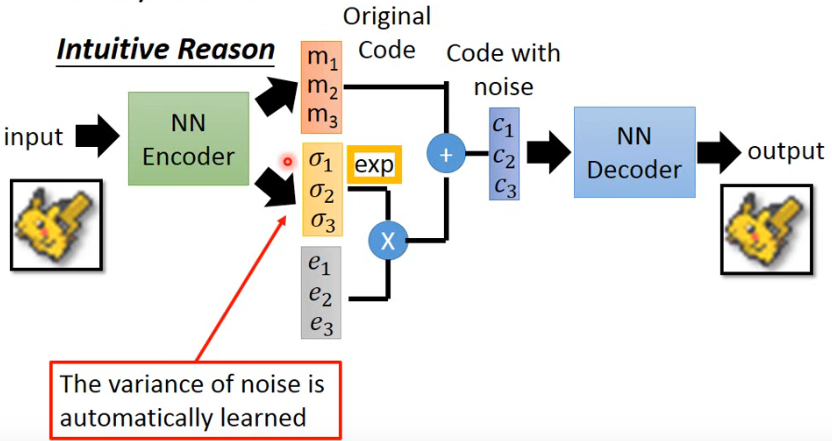
• 这里的 m 就是原来 AE 中的 code，而 c 是加上 noise 之后的 code。下面这些 vector 就是 noise，黄色的 代表 noise 的 variance，但由于不能确定正负，为了保证 variance 是正的，因此加了一个 exp 过程，灰色的 是从一个 normal distribution 中采样出来的 vector。

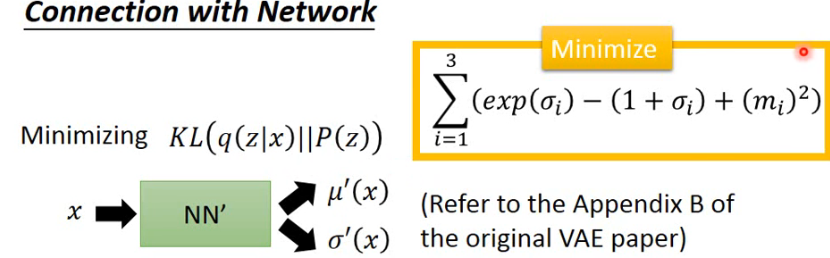
但如果我们只是想 minimize reconstruction error 的话，这是不够的，train 出来的结果并不是预期的样子。因为这里的 variance 是让 machine 自己学的，那 machine 肯定是想让它成为 0 就好了，这时就退化成原来的 AE。所以为了防止这一件事，我们还需要加一个限制，限制这个 variance 不能太小，而我们加的 minimize 的另一个式子（下图的右下角的黄色）就是为了做这一件事：

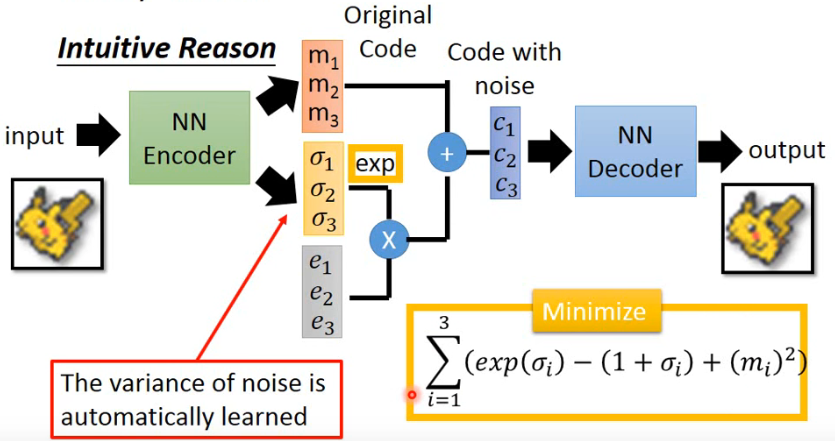
这一项式子是什么意思呢？

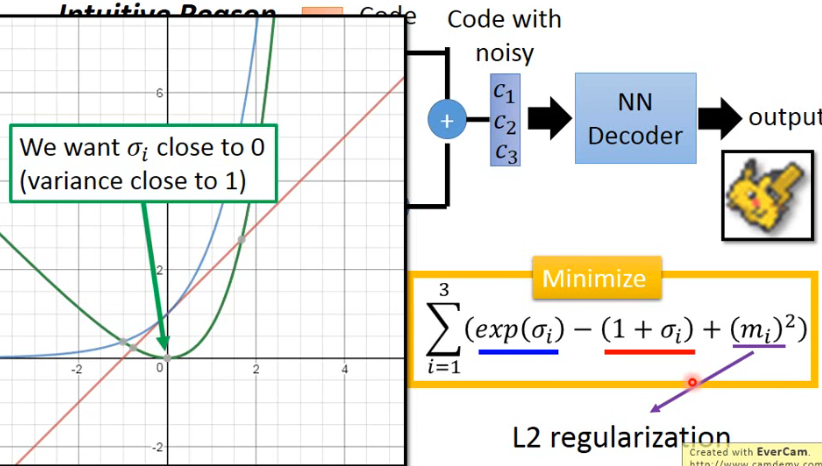
• 式子中蓝色画线的部分如左图中的蓝线，红色画线部分如左图中的红线，两条线的差值就是绿色的线，可以看到绿色最小值处就是 的时候 loss 最低，所以我们 minimize 这个式子就是想让 接近 0，从而 variance 能够接近 1，这样就限制了 variance 不会太小。
• 紫色画线的式子就是可以理解为对 code 做一个 L2 的 regularization，可以让它的结果比较 sparse，比较不会 overfitting。

以上就是对 VAE 的一个直观的理由。下面就是一个正式的理由了，就是 paper 中比较常见的说法了。

回到说我们到底想要做什么。每一个 Pokemon 是 space 中的一个 point x，我们想做的就是估计 X 的一个 probability distribution：

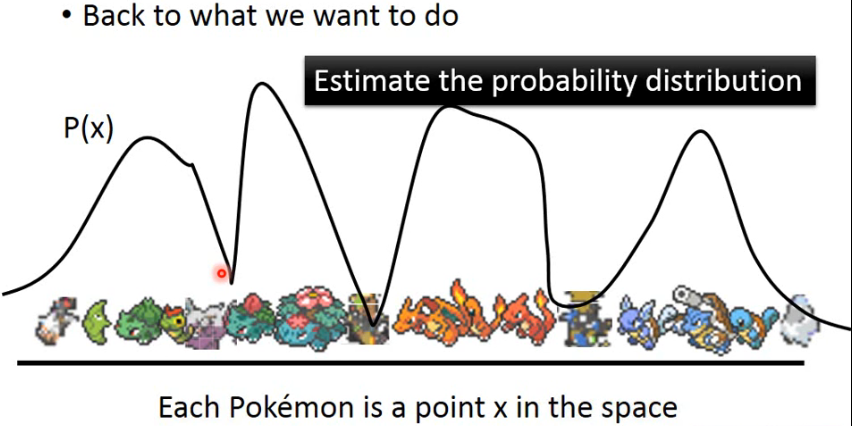
• 我们要做的就是 estimate 这个 。如果我们知道了 P(X) 的样子，那我们就可以根据这个 distribution 去 sample 出一张 image，它就会像是一张 pokemon 的 image，因为你在 sample 的时候会很有可能从高概率的地方去 sample；
• 在这个 distribution 中，pokemon 的 image 所对应的 x 处 P(x) 会高，而那些不知道什么东西的 x 的 P(x) 就会很低。

2.2 GMM

怎样去 estimate 一个 probability distribution 呢？我们可以用 Gaussian Mixture Model（GMM）。它长这个样子：

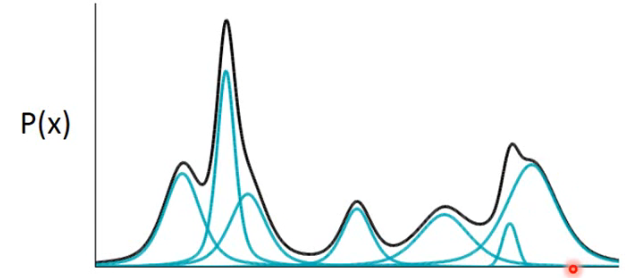
• 这个黑色曲线就是 GMM 的 distribution，它很复杂，它其实是用很多 Gaussian 用不同的 weight 叠合起来的结果，只要你今天 Gaussian 的数目够多，就可以产生很复杂的 distribution。

那这个式子该怎么写呢？看看我们怎样从一个 GMM 中 sample 出一个 x 出来。假设我们现在有一把 Gaussian，每个 Gaussian 背后有它自己的一个 weight，然后你要根据这些 Gaussian 的 weight 去选择从哪一个 Gaussian 来 sample data，然后再从这个所选择的 Gaussian 中进行 sample 出一个 data point：

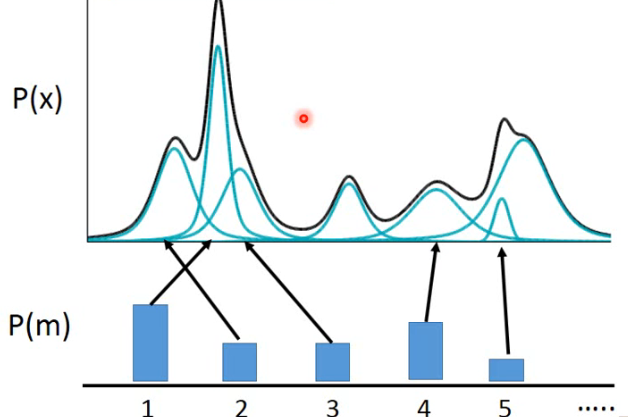
所以这个 sample 的公式如下：

• 先从一个 multinomial 的 distribution 中 sample 出一个 m，表示要从哪个 Gaussian 中 sample data；
• 然后根据所选择的 Gaussian 的 mean 和 variance 来 sample 出一个 x。

合起来，GMM 就是下面：

• 这个 P(x) 就写成了 summarization over 所有的 Gaussian，那个 Gaussian 的 weight P(m) 再乘上有了那个 Gaussian 以后从那个 Gaussian 中 sample 出 x 的几率 P(x|m)。

GMM 其实也有种种的问题，比如你需要决定 mixture 的数目，当你决定了 mixture 的数目，再给你一些 data x，你要 estimate 这一把 Gaussian 的对应的 weight 和 mean、variance，这只需要用 EM 算法就可以了。

现在每一个 x 其实都是从一个 mixture 中 generate 出来的，这就有点像 classification 一样，每一个 x 都来自于一个 class。但我们也学过，对 data 做 classification、做 clustering 是不够的，更好的表示方式是用 distributed representation，也就是说每一个 x 它不是说属于某一个 class 或某一个 cluster，而是它有一个 vector 来描述它所面向的各个不同的 attribute。所以 VAE 其实就是 GMM 的 distributed representation 的版本。

2.3 从 GMM 到 VAE

说 VAE 是 distributed representation 版的 GMM，是怎么一回事呢？

首先我们要从一个 normal distribution 中 sample 出一个 vector ， 这个 vector 的每一个 dimension 都代表了你现在所要 sample 的那个东西的某种 attribute。我们接下来的画图时会假设 z 是一维的，但在实际中它可能是 10 维、100 维的，这取决于你。现在我们 sample 出 z 以后，根据这个 z，我们可以决定 Gaussian 的 mean 和 variance。与刚刚 GMM 进行类比，GMM 是有限个 Gaussian，而这里的 z 可以是无穷多个，那也可以有无穷多个 Gaussian。

怎样根据 z 来决定这个 Gaussian 的 mean 和 variance 呢？这可以是一个 function， 就代表给一个 z 以后它的 mean 是多少， 就代表给一个 z 以后它的 variance 是多少。这个如下图所示：

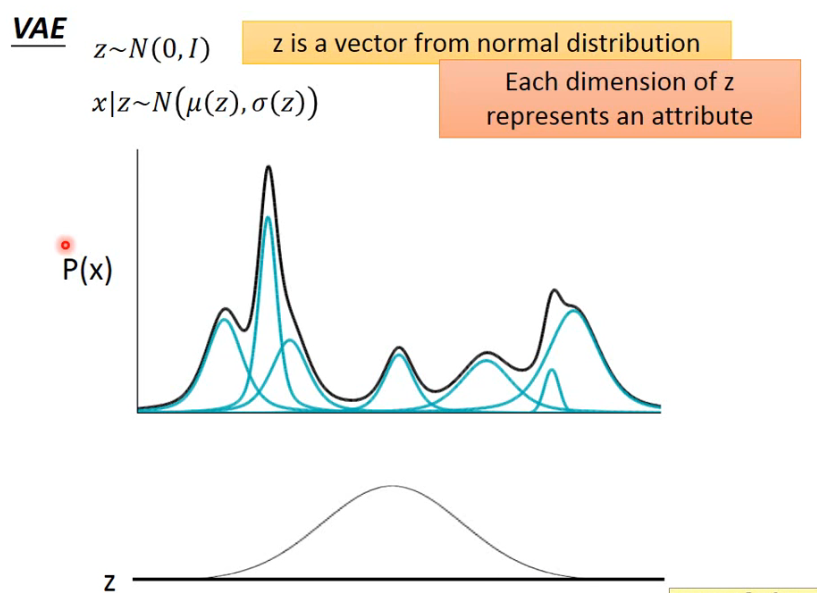
看一下实际上这个 P(x) 是怎样产生的。在 z 这个 space 上每一个点都有可能被 sample 到，只不过中间高的地方容易被 sample 到，z 这个 space 中的每一个点都对应一个 Gaussian：

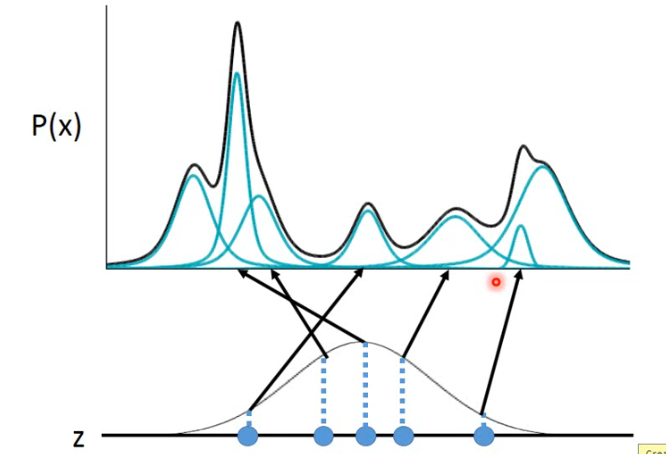
但每一个 point z 具体对应到一个什么样的 Gaussian 呢？它的 mean 和 variance 可以通过一个 z 的 function 来得到，而 neural network 本身就是一个 function，因此可以通过 train 一个 NN 来拟合这个 function：

那现在 P(x) 的式子长什么样了呢：

• 因为 z 的 continue 的，所以这里要用积分。

有人或许会困惑 z 的分布为什么一定要是个 Gaussian 呢？它确实也是可以是一朵花的样子，它的形状可以是你假设成任何形状。但由于用来得到 和 的 NN 是非常 powerful 的，所以：Even though z is from N(0, 1), P(x) can be very complex.

既然通过一个 NN 来将 z 映射到 和 ，那这个 NN 该怎样去 train 呢？这可以通过 maximizing the likelihood of the observed 来训练：

另外我们还需要引入另外一个 distribution ，它跟上面说的这个 NN 是相反的，上面这个 NN 是 given z 来获得决定 x 的 mean 和 variance，但刚引入的这个 q(z|x) 是 given x 得到决定 z 这个 space 上面的 mean 和 variance，也就是决定 z 从什么样的 mean 和 variance 的 Gaussian 中 sample 出来：

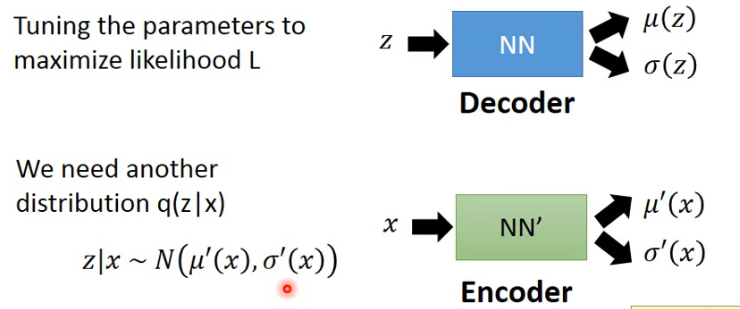
• 其实上面这个就是 VAE 中的 Decoder，下面这个就是 VAE 中的 Encoder。

先不管这个 NN，对 还可以进入如下的改写与推导：

• 这个 q(z|x) 可以是任何一个 distribution，就可以当它是一个从大街上捡来的 distribution；
• 第一步等号：其实什么也没有做，将右边的 提出来之后，对 z 进行积分就等于 1，所以就什么也没有做；
• 第二步等号：其实也什么都没做，只是将 P(x) 改写了一下；
• 第三步等号：也什么都没做，分子分母同时加了个 q(z|x) 然后又拆开的；
• 第四步等号：就是将 log 里面的乘法拆成了两个 log 的加法；
• 第三行的等式中，后面一项称为 KL divergence，它衡量了两个 distribution 之间的接近程度，值越大代表越不像，当相同时 KL divergence 等于 0；
• 由于 KL 大于等于 0，因此可以推出第四行的这个不等式，第四行的式子就是对第三行等式第一项的一个改写，它被称为 lower bound 。

经过上面推导，现在我们要 maximize 的 log probability，也就是要 maximize 的对象 就是 lower bound 和 KL 加起来的结果：

其中 长这个样子：，在这个式子里面，P(z) 是一个 normal distribution，是一个已知的，不知道的是 P(x|z) 和 q(z|x)。

回头看一下 ，我们本来要做的是通过调节 P(x|z) 来 maximizing log likelihood ，但现在我们要同时寻找 P(x|z) 和 q(z|x) 一块来 maximizing ，为什么突然要多找一项 q(z|x) 呢？因为假如说你只调节 P(x|z) 来 maximizing 的话，我们知道 只是 log likelihood 的一个 lower bound，也许你期待你的 lower bound 上升的时候，log likelihood 也跟着一块上升，但是一个比较糟糕的情况是，尽管你的 lower bound 在上升，但你的 log likelihood 反而是在下降的。现在我们引入 q(z|x) 就可以解决这个问题。如下图：

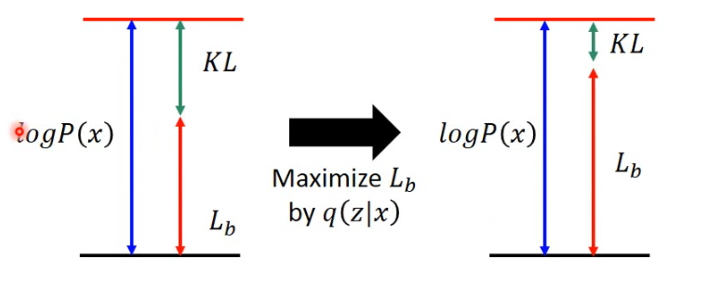
• 本来这个 q(z|x) 是与 一点关系都没有的，因为按照等式，log P(x) 只跟 P(x|z) 有关，所以 q 这一项不管是什么值，上面这条红线 log P(x) 的值都是不变的，也就是蓝色箭头这个长度都是不变的。
• 现在假如我们固定住 P(x|z) 而只通过调节 q(z|x) 来 maximize 的话，你会让 一直上升，最后 KL 会特别特别小，甚至完全不见，这样 lower bound 就和 log likelihood 一样大了，之后你再让 lower bound 增大的话，log likelihood 就一定会增大了，这也就解决了刚刚那个问题。
• 一个有趣的是，刚刚做的那件事会得到一个副产物，由于 KL 越来越小，所以这里 KL 所衡量的两个分布 q(z|x) 和 p(z|x) 越来越接近。

所以经过上面讨论，我们寻找 P(x|z) 和 q(z|x) 来让 maxmizing ，而这也等同于 maximizing log likelihood，同时找到的这个 q(z|x) 也是一个 p(z|x) 的 approximation。

那 长什么样子呢：

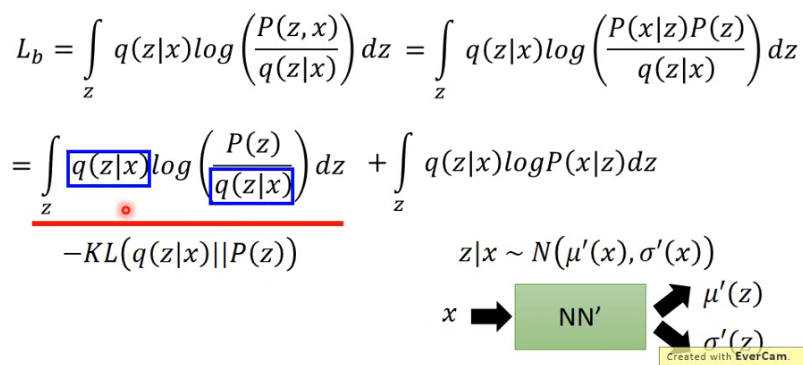
• 也是做一下简单的变换就可以得到；
• 这里面的 q(z|x) 与 P(z) 的 KL 散度中，q 其实是一个 Neural Network ，当你给一个 x 的时候，它会告诉你说这个 q(z|x) 是从什么样的 mean 和 variance 的 Gaussian 中 sample 出来的。

所以如果你要 minimizing KL(q(z|x) || P(z)) 的话，你就是调 q 所对应的那个 Neural Network ，就是调这个 NN’，希望它产生的 distribution 跟 normal distribution P(z) 越接近越好。这件事情的推导可以参考 VAE 的原始 paper。这里要 minimize KL(q(z|x) || P(z))，其实就是要 minimize 下面黄色方框的部分中，这个式子就是我们在直觉解释 VAE 中提到的所要 minimize 的：

还有另外一项：，所以我们还要 maximizing 这一部分：

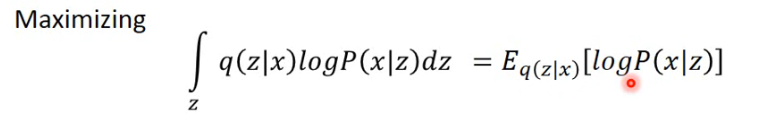
• 这一步等式就可以想象成我们有一个 log P(x|z)，然后它用 q(z|x) 来做 weighted sum，所以可以写成 这样一个期望值的形式，所以这个式子的意思就是说我们给我们一个 x，从 q(z|x) 这个几率分布中 sample 出 data，然后靠 sample 的 data 让 log P(x|z) 越大越好。

这件事情其实就是 Auto-Encoder 做的事情：

• 怎样从 q(z|x) 中 sample 一个 data 呢？就可以把一个 x 丢进 NN’ 中，它产生一个 mean 和 variance，然后根据这个 mean 和 variance 就可以 sample 出一个 z；
• sample z 做完后，接下来就是要 maximize 这个 z 产生 x 的几率 ，这个 z 产生 x 的几率就是把 z 丢进上图中蓝色的这个 NN 中，它 output 出一个 mean 和 variance。要怎么样让这个 NN output 所代表的这个 distribution 产生 x 的几率越大越好呢？如果我们无视 variance 这一项的话（实践中通常这么干），你要做的就是让 NN output 的 mean 跟 x 越接近越好，因为 Gaussian 中 mean 处的几率是最大的。

所以现在这整个情况就变成了说：input 一个 x，NN’ 产生两个 vector，sample 一下产生一个 z，然后你要根据这个 z 来产生另外一个 vector，这个 vector 要跟原来的 x 越接近越好。所以这件事其实就是 Auto-Encoder 在做的事情。

2.4 Conditional VAE

VAE 还有另外一件事叫做 Conditional VAE，它可以让 VAE 产生手写的数字，比如给他一个数字 4 的 digit image，他能产生一系列的这个 style 的其他 digit 的 image：

VAE 更多资料

2.5 Problems of VAE

VAE 的一个问题是，It does not really try to simulate real images. 比如下面这张图：

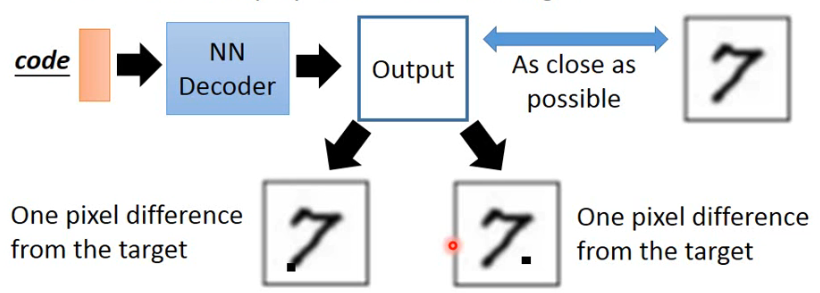
• 在 VAE 产生的下面两张 image 中，虽然你只有一个 pixel 是不一样的，但是人一眼看上去就容易看出第二张是 machine generated，但这两张 image 对 VAE 都是一样好或者一样坏。

所以 VAE 学的是怎样产生一张 image 与 database 里面的 image 一模一样，但他从来没有想过真的产生一张可以以假乱真的 image，它只是在模仿而已，它没有产生新的 image。因此这也有了后面的 GAN 等。