 Deep Reinforcement Learning
Deep Reinforcement Learning
强化学习在新版课程中已经有讲解了,这里是老版课程的笔记,其中介绍了 PPO 以及 Deep Q Learning 的 RL 方法。关于 RL 的基本知识,这里就不再重复了。
# 1. RL 中的困难
RL 中主要有两个难点:
- Reward delay:一个 game 中,很多 action 并不能立刻取得游戏分数,但对 Actor 在之后取得游戏分数至关重要。比如 space invader 游戏中,左右移动并不会获得分数,只有 fire 动作会获得分数,如果仅仅将游戏奖励当作 RL 的 reward,那训练的 Actor 会倾向于一直 fire 而不在左右移动。
- Agent’s actions affect the subsequent data it receives:Actor 的 action 会影响它接下来所看到的画面,所以在 RL 中,让 Actor 能探索没有做过的行为,是一件很重要的事情。
# 2. Outline
# 2.1 Policy-based 和 Valued-based

- 在 Policy-based 的方法中,会 learn 一个负责做事情的 Actor
- 在 Valued-based 的方法中,会 learn 一个不做事情的 Critic,它专门批评
- 要把 Actor 和 Critic 加起来的,叫做 Actor-Critic 方法
截止上课时,当前最新的 A3C 就是 Asynchronous Advantage Actor-Critic 方法。
# 2.2 RL 也是寻找一个 Function
RL 中的 Actor 在决定采取 action 时,其实就是:
有些 paper 中也称这里面的 Actor 为 Policy
RL 的过程可以看成三步:
- Neural network as Actor
- 决定一个 Actor 的好坏
- 选一个最好的 Actor:Gradient Ascent
# 1)Neural network as Actor
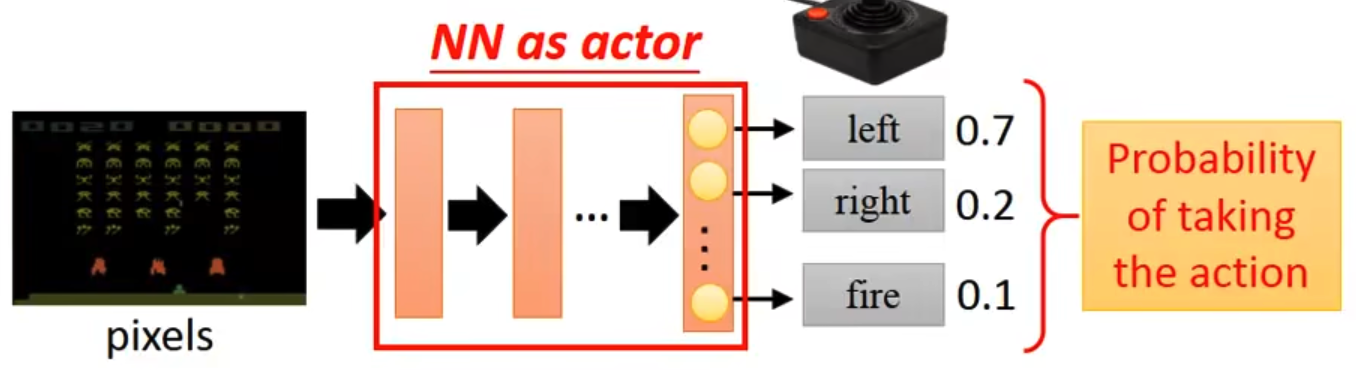
相比于 lookup table,使用 NN 作为 actor 能够具有更好的泛化性。
# 2)决定一个 Actor 的好坏
这里用 actor
让 actor 去玩一个 game,用
对于同一个 actor,尽管每次采取相同的 actions,也有可能得到不同的 total reward。所以我们定义
所以,
一个 episode 可以视为一个 trajectory
当一个 actor 确定后,
可以想象,不同的人来玩同一个游戏,得到的 trajectory 大概率服从的概率分布也是不同的
这样,expected value 就可以这样计算了:
理论上,可以 sum over all possible trajectory,但实际中,你只能让 actor
# 3)选一个最好的 function:Gradient Ascent
既然知道了怎样衡量 actor,那就可以选出一个最好的 actor。
做法就是:Gradient Ascent
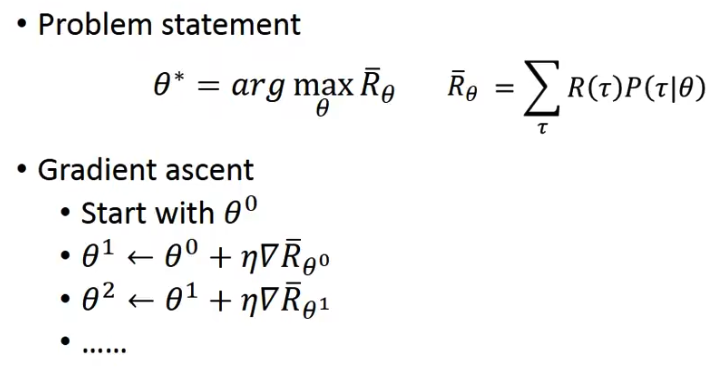
这里的
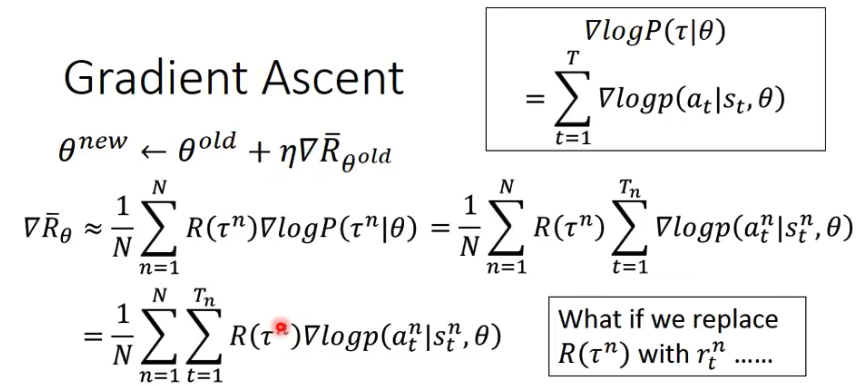
除此之外,可能还需要给公式中的
# 3. PPO
# 3.1 on-policy 到 off-policy
on-policy 和 off-policy 两种 training 方法的区别如下:
- on policy:The agent learned and the agent interacting with the environment is the same.
- off policy:The agent learned and the agent interacting with the environment is different.
在 on-policy 方法中,我们会使用 actor
思路:使用另一个 actor

# 3.2 Importance Sampling
在具体讲解之前,需要先看一个比较泛用的技术:Importance Sampling。
我们在计算 f(x) 在概率分布 p(x) 下的期望时,往往可以从 p(x) 概率分布中采样出一堆
但如果我们不能从 p(x) 概率分布中做采样的话,那这里就不能这样计算了。可以使用一个技巧做一下转换:
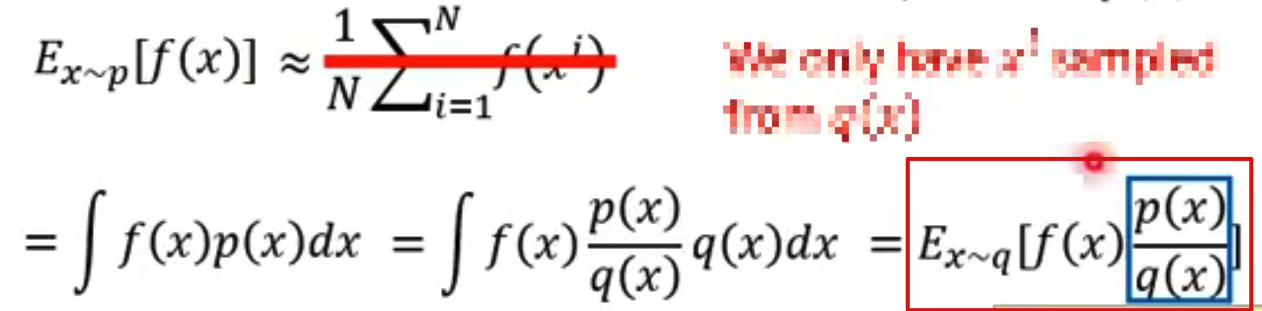
可以看到经过转换,期望的计算只需要能够从另外一个分布 q(x) 中做采样就好了,而不需要从 p(x) 做采样。
尽管理论上可以这么等价,但是在实际中并不能随便选一个 q(x) 概率分布,而是要求 q(x) 与 p(x) 不能差太多。感性上的原因是:以上公式中计算期望是等价的,但这两个的方差却是不同的,当方差差距过大的时候,采样数据量不足的话可能会让结果出现很严重的偏差。因为我们计算期望不是直接计算的,而是通过采样来估计的,方差差距过大会让这种估计变得很不稳定。
# 3.3 使用 Importance Sampling 后

将上面的

于是有了
# 3.4 PPO 1:近端策略优化惩罚
Proximal Policy Opetimization(PPO)
但前面因为使用了 Importance Sampling,所以

这样也就限制了训练出来的
PPO 的前身有一个 TRPO 方法,他的 objective function 直接就是
,同时另外把 当做了额外的限制条件,但这样的优化问题就难以来实施了,所以不如 PPO 那样直接把 constrants 写进了 objective function 中更容易实践。
注意,这里的 KL 计算的是两个 actor 的 behavior 的差距,而并非只是简单的两个参数的距离。
PPO Algorithm:

可以看到,与 on-policy 的训练方法明显不同的一点就是,这里在 collect 一批 data 后,可以用来多次 update parameters。
KL 惩罚项的系数
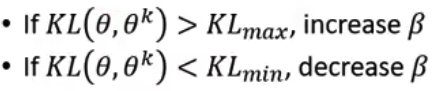
如果 update 后 KL 差距过大,说明 KL 惩罚项起到的作用较少,这时候应该增大惩罚项的作用,反之亦然。
另外,这里的 KL 的计算也是 sample 出一大堆数据来计算。
# 3.5 PPO 2:近端策略优化裁剪
PPO 算法还有另一种实现方式,不将 KL 散度直接放入似然函数中,而是进行一定程度的裁剪。
这种实现方式中,公式看着很复杂,但是想要表达的思想特别直观。PPO 2 的算法如下:
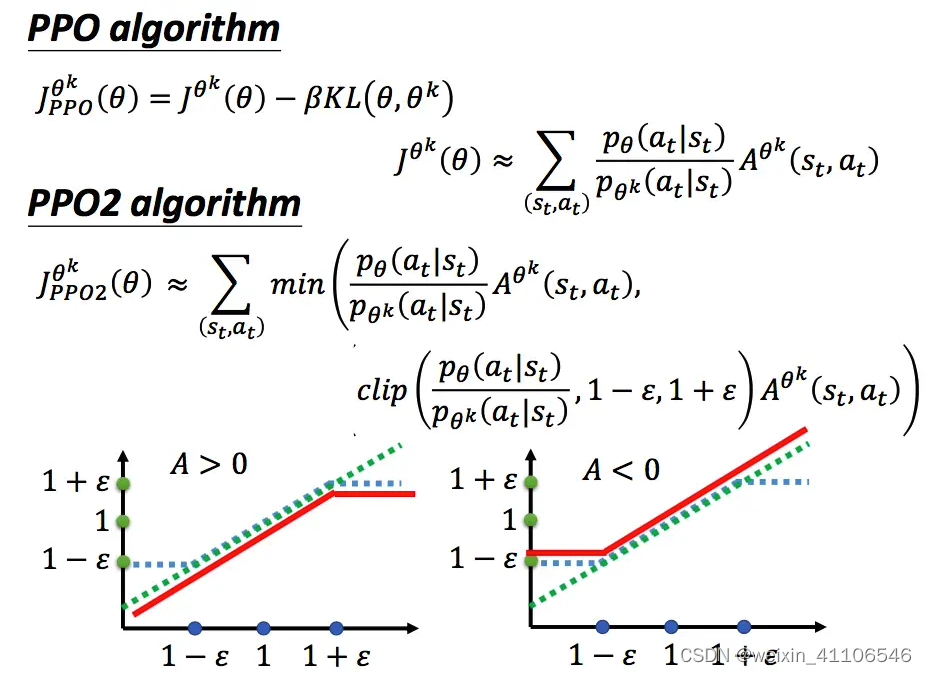
可以看到,这个 objective function 是一个 min 函数,包含两项,下半部分的坐标图的横轴代表
上式看起来很复杂,其实很简单,它想做的事情就是希望
- 操作符 min 作用是在第一项和第二项中选择最小的。
- 第二项前面有个裁剪(clip)函数,裁剪函数是指:在括号里有三项,如果第一项小于第二项,则输出1 − ε;如果第一项大于第三项的话,则输出1 + ε。
- ε 是一个超参数,要需要我们调整的,一般设置为0.1或0.2 。
坐标图中,红色的线就是整个 min 函数的值,可以看到,当 A 大于 0 时,我们自然希望
以上就是 PPO 的算法。
