 k 近邻法
k 近邻法
# 1. k 近邻法简介
# 1.1 KNN 的直观理解
k 近邻(K-Nearest-Neighbor,KNN)的简单想法是,我们如果对某一个新的实例感兴趣时,根据它最近的 k 个邻居来判断即可。
k 近邻法(KNN)是一种基本的分类与回归方法。主要思想是:假定给定一个训练数据集,其中实例标签已定,当输入新的实例时,可以根据其最近的 k 个训练实例的标签,预测新实例对应的标注信息。
- 用于分类问题:对新的实例,根据与之相邻的 k 个训练实例的类别,通过多数表决等方式来进行预测,哪一类别的占比达,新的实例点就属于哪个类别;
- 用于回归问题:对新的实例,根据与之相邻的 k 个训练实例的标签,通过均值计算进行预测。
举个例子,下面的图形给定了 11 个观测值,包含 6 个蓝色正方形和 5 个红色三角形,这就是我们的训练数据集:

假如现在给定一个新的实例点(也即是中间那个绿色的圆点),它该属于哪个类别呢?当选定 k = 3 时,最近的 3 个邻居中红色三角形占得最多,因此预测新实例点为红色三角形类;当选定 k = 5 时,最近的 5 个邻居中蓝色矩形占得最多,因此预测新实例点为蓝色矩形类。
所以,多少个邻居,怎么计算距离,如何通过邻居的情况反映目标点的信息,都是非常关键的问题。
# 1.2 KNN 的具体算法
输入:训练集
输出:新实例 x 所属的类别 y
具体来说,算法包含三部曲:
- 给出「距离度量」的方式,计算新的 x 与训练集 T 中每个点的距离;
- 找出与 x 最相近的 k 个点,将涵盖这 k 个点的 x 的邻域记作
- 根据「分类决策规则」来决定 x 所属的类别 y,即:
其中
我们刚刚强调的三个事情:距离度量、k 个邻居、和分类决策规则就是 k 近邻法的三要素。注意:任意一者的变化,都可能导致实例 x 所属的类别发生变化。
# 1.3 KNN 的误差率
本部分的证明过程可以先略过
训练集:
类别集合:
考虑最近邻法:就是指 k=1 的情况
对于新实例
计算分类不正确时的误差率:
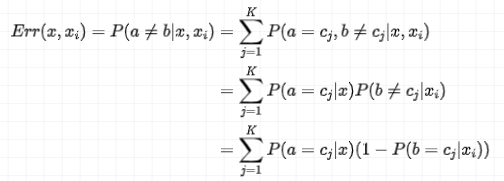
因为事件
接下来看一下
当
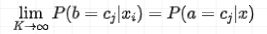
此时,有:
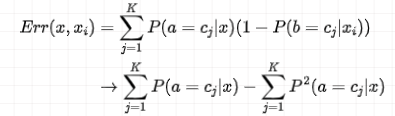
可见,第一个求和式等于 1,那么公式可写成:
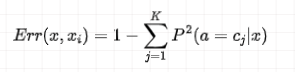
假设 x 的真实类别为
也就是说,希望找到一个
对应的贝叶斯误差率为:
回到最前所讲的 k 近邻法误差率第二项:
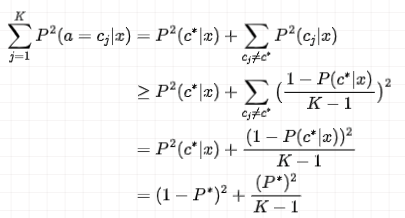
如果想使这个式子的第二项
误差率:
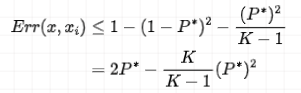
当
此处给大家说的这个误差率考虑的是最近邻法,也就是 k=1 的时候。如果推广到 k 近邻法,可以令 N 趋近于无穷大,K 也无穷大,也就是训练数据集中包含了无穷多个样本,而且输出空间也包含了无穷多个类别。
此时的误差率应该趋于
# 2. k 近邻法的三要素
k 近邻法虽然没有显性模型,但也是具有决定模型的三要素的。由于 k 近邻法就是要找到目标点的 k 个邻居,然后再做决策,所以找多少个邻居,怎么找邻居,以及找到邻居后怎么办是非常重要的。
实际上,这就涉及到空间的划分,俗称划地盘,具体来说就是先拿到训练数据集,然后对特征向量空间进行划分。
# 2.1 k 近邻法的 feature space
举个大家都熟悉的例子,二维平面,也就是数据集对应的特征空间是二维的。
假如训练数据集中包含两类数据,一个是「点类」,一个是「叉类」,我们可以给每个训练实例都划分出个小地盘出来,也就是图中形状各异的格子。我们通过最简单的最近邻法来说明,也就是当 k=1 时的情况。
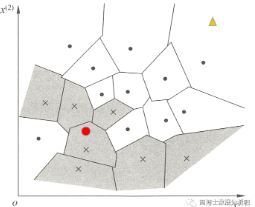
得到这些小格子后,咱们就可以对每一个新的实例点做出判断,预测它的类别了。现在我们以「红点为例」,距离它最近的训练实例点是下边的小叉叉,那么「它的类别属于叉类」,同样,以「黄色小三角为例」,距离它最近的训练实例是圆点,「类别属于点类」。
那么这些小格子怎么画出来的呢?或者说这一个个子空间怎么确定出来的呢?这就得考虑 k 近邻法的三要素了:距离度量、 值的选择、分类决策规则。
# 2.2 三要素之一:距离度量
Lp 距离
feature space
特征空间中任意的
✨ 1. p = 2 时,称为欧式距离(常见的勾股定理就是二维时的它):
✨ 2. p = 1 时,称为曼哈顿距离(也就是计算所有特征下的绝对距离,再求个和):
✨ 3. p =
下面我们通过一个二维的例子来说明当 p=1、p=2、p=
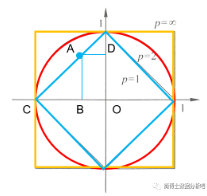
由此可见,当采用的不同的 p 时,距离也会发生变化,那么这时候能找到的最近的邻居自然也不同了。
# 2.3 三要素之一: k 值的选择
对于一个新实例点,当 k 值不同时,所属的分类也会不同。例子之前讲过:

- 对于新实例点绿色圆圈,按照多数表决规则:当 k=3 时,它是红三角类型;当 k=5 时,它是蓝正方形类型。
如果选择的 k 值比较小,相当于就在一个比较小的邻域里面对训练集内的实例进行预测,所以近似误差小(也就是说对 training set 的拟合误差小),但是如果新增一个实例时,超过了范围则会导致估计误差增大,即对噪声很敏感。这就是只对训练集友好,对新的实例点不友好的情况——过拟合。与之相对,k 值较大时,就会出现欠拟合。整理如下:
| 特点 | k 值较小 | k 值较大 |
|---|---|---|
| 近似误差 | 小 | 大 |
| 估计误差 | 大 | 小 |
| 敏感性 | 强 | 弱 |
| 模型 | 复杂 | 简单 |
| 拟合程度 | 过拟合 | 欠拟合 |
Tips
- k 值可通过交叉验证选择。
- k 值一般低于训练集样本量的平方根。
# 2.4 三要素之一:分类决策规则
多数表决规则:由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。
分类函数:
这个函数的意思是 f 每吞进去一个 n 维向量的实例,就得吐出来一个类别。
为了制定一个规则决定这个分类函数,我们需要比较损失情况,因为是分类问题,这时候最常用的损失函数是 0-1 损失函数:
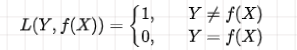
其中
那么误分类的概率就表达出来啦。0-1 误分类概率:
假如给定实例
可以将所有的
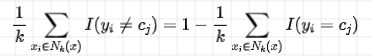
上面这个误分类率就是指对于某一个实例
这就体现出了多数表决规则啦!
# 3. kd 树的构造和搜索
假如我们现在有一个数据集,当给定一个新的实例时,最简单粗暴的办法就是计算它和所有点的距离,然后找到 k 个最近邻,最后根据多数表决的规则判断这个实例所属的类。
但是如果这个数据集中的训练实例非常多且密集呢?如果数据集中有成千上万个点,那每运算一个点的类型都要经过巨大的额运算,这样的运算量是极大的:
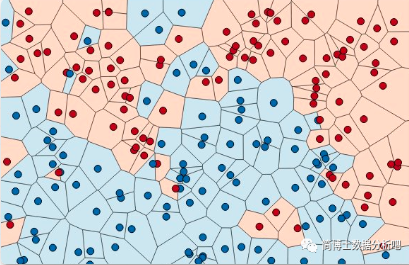
这时,我们就可以用一个更快速的计算办法 —— kd 树。
# 3.1 什么是 kd 树?
THEOREM
kd 树是一种对 k 维空间中的实例点进行储存以便对其进行快速检索的树形数据结构。
从本质上来看,kd 树是一个二叉树,根据这个结构对 k 维空间进行不断的划分,每一个节点就代表了 k 维超矩形区域。
注意,这里 kd 树的 k 指的是是特征的个数,也就是数据的维度,而之前 k 近邻法中的 k 指的是距离新实例点最近的 k 个邻居。
举个例子,二维(k=2)的划分区域:
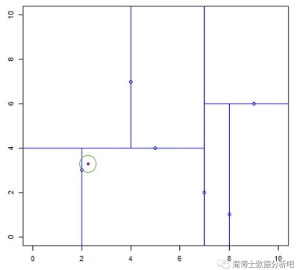
三维(k=3)的划分区域:
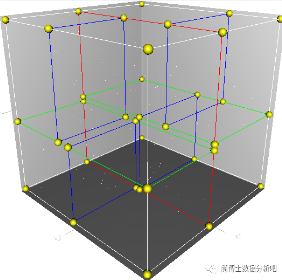
# 3.2 如何构造 kd 树?
「输入」:k 维空间数据集
「输出」:kd 树
👣 1. 开始:构造根节点
以
👣 2. 重复:剩余特征的选取与切割
继续对深度为 j 的结点,选择
👣 3. 停止:得到 kd 树
直到两个子区域没有实例时停止分割,即得到一棵 kd 树。
# 3.3 kd 树构造示例
现在我们按照上面的思路一起来构建一棵二维的 kd 树。
「输入」:
数据的散点图如下:
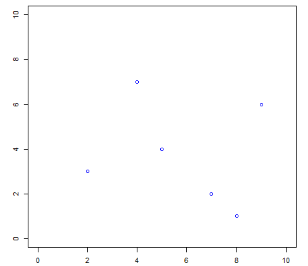
因为该训练数据集的维度为 2,那么任选一个特征即可。不妨选择
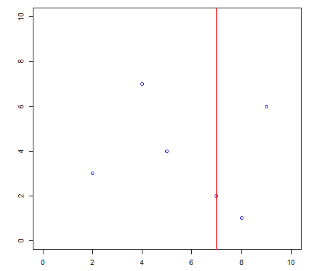
左边的就是在
下面进行第 2 次切分,以
同样的,对第一次切分后的右边区域而言也进行如此切分,选择 (9,6) 为切分点进行第二次切分。切分后的图为:
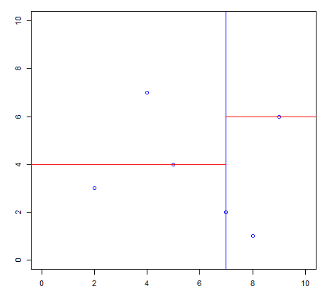
我们将切分后的四个区域分别以 A B C D 命名:
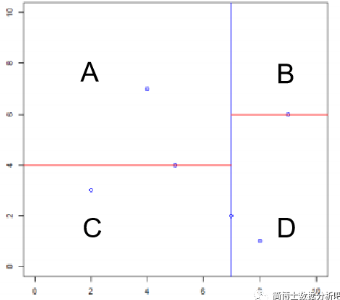
可以看到 ACD 三个区域中还有一个实例点,那么过这些点继续画一条垂直于
至此,切分均已完毕:
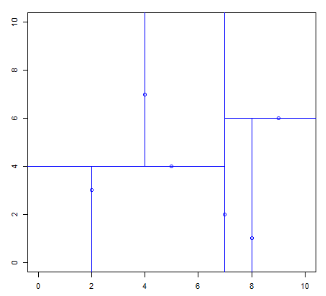
根据这个层次可以绘制出 kd 树:

# 3.4 如何搜索 kd 树?
「输入」:已构造的 kd 树,目标点是 x
「输出」:x 的最近邻
👣 1. 寻找“当前最近点”
从根结点出发,递归访问 kd 树,找出所划分的区域内包含 x 的叶结点,以此叶结点为“当前最近点”。
👣 2. 回溯
以目标点和“当前最近点”的距离沿树根部进行回溯和迭代,当前最近点一定存在于该结点一个子结点对应的区域,检查子结点的父结点的另一子结点对应的区域是否有更近的点,如果更近则更新“当前最近点”。
当回退到根结点时,搜索结束,最后的“当前最近点”即为 x 的最近邻点。
看不懂没关系,接下来看到例题就都明白啦!
# 3.5 搜索 kd 树示例
还是以刚才生成的那棵 kd 树为例:

# Example 1
「输入」:kd 树,目标点 x=(2.1, 3.1);
「输出」:该目标点的最近邻点
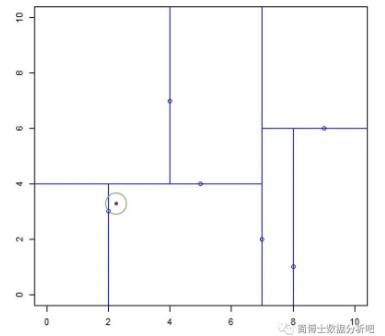
寻找当前最近点:从根节点开始,x=(2.1, 3.1) 在根节点 (7, 2) 的左子区域内,继续到 (5,4) 所确定的左子区域内,继续到 (2, 3) 的右子区域中,(2, 3) 就是当前最近邻点。
回溯:我们以 (2.1, 3.1) 为圆心,以两点之间的距离为半径画一个圆,这个区域内没有其他的点,那就证明 (2, 3) 是 x=(2.1, 3.1) 的最近邻点。
# Example 2
「输入」:kd 树,目标点 x=(2, 4.5);
「输出」:该目标点的最近邻点
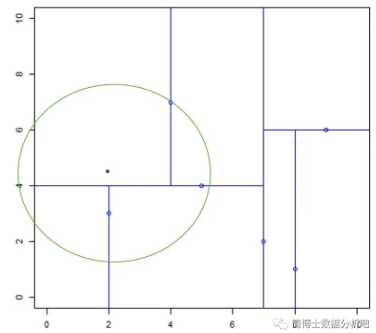
- 寻找当前最近点:从根节点开始,x=(2, 4.5) 在根节点 (7,2) 的左子区域内,继续到 (5,4) 所确定的上子区域内,继续到 (4,7) 的左子区域中,(4, 7) 就是当前最近邻点。
- 回溯:我们以 (2, 4.5) 为圆心,以 (2, 4.5) 到 (4,7) 两点之间的距离为半径画一个圆,这个区域内有两个节点,分别是 (2,3) 和 (5,4),通过计算 (2, 4.5) 到这两点的距离,得出到 (2, 3) 的距离最近,那么 (2, 3) 就是最近邻点。接着,再以 (2, 4.5) 为圆心,以 (2, 4.5) 到 (2, 3) 两点之间的距离为半径画一个圆,此时圆里没有其他的节点,说明可以确认 (2, 3) 就是 (2, 4.5) 的最近邻点。
