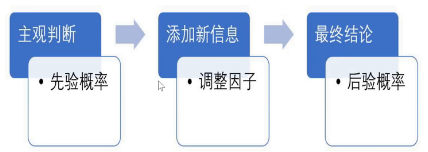
贝叶斯思维和我们人类做判断的思路是相似的，都是按照主观判断、添加新信息、最终结论三步骤进行，换成数学思维里就是先验概率、调整因子、后验概率。

比如今天是冬至，你走到餐馆里，老板根据今天的节气做出一个主观判断，会问你“要不要来盘饺子”，因为大多数人在冬至这一天会选择吃饺子。但如果你用宝儿姐的四川话回一句“我今天不吃饺子”，那这句话其实相当于在原有的基础上提供了新的信息，老板根据新提供的信息可能会判断出你是个四川人，于是会问你“要不要来碗羊汤”，因为四川人在冬至这一天会选择喝羊汤。如果你说好，那就是老板成功预测出今天你打算喝羊汤这个最终结论。

上面例子的整个过程用 Bayes 思维表述就是：

1. 朴素贝叶斯定理

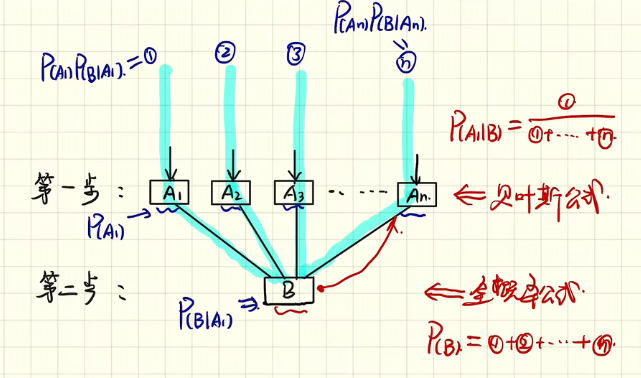
1.1 Bayes 定理

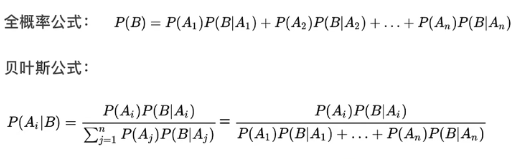
1.2 Bayes 分类

存在 K 类：，给定一个新的实例 ，问：该实例归属于哪一类？

由 Bayes 公式知 ，所以我们可以分别计算 的值，然后找到最大的那一个，从而就可以确定归属的类了。

公式也可以写成：

那么什么是朴素 Bayes 呢？

1.3 Naive Bayes

朴素贝叶斯和贝叶斯相比，做了一个“朴素”的假设：特征与特征之间是相互独立、互不影响的。

这样我们回到 Bayes 分类的

公式中，因为所有的 与 在 时相互独立，那么 就可以写成：

所以最终只需要求出：

从而找到了归属的类别，完成了朴素贝叶斯法的分类。

2. 朴素贝叶斯法的学习与分类

之前介绍了朴素贝叶斯法，它常用于解决分类问题，所以就有了朴素贝叶斯分类器，从根本上来说它就是一种「分类方法」。这一节我们继续说说，朴素贝叶斯因何而朴素，它的判断准则又是什么呢？

2.1 如何理解“朴素”？

首先来看一个训练数据集，计算得出一个联合概率分布。

已知训练数据集

输入：，

输出：，

生成方法：学习联合概率分布

注意这里是用了“生成方法”，这种方法首先学习联合概率分布 ，得到条件概率分布 ，即生成模型，比如朴素贝叶斯法和隐马尔可夫模型。

接下来，我们就一起看如何求出联合概率分布。

X 是 feature，Y 是所属类别， 叫做先验概率分布， 叫做条件概率分布，而 叫做后验概率分布。

联合概率分布可以通过先验概率分布乘以条件概率分布得到。

为什么要“朴素”呢？

2.2 为什么要有条件独立性假设？

以“帅是怎么定义的”为例，可以根据“身高、体重、脸型、鼻型”列一个表格，在“身高”中，高于 170cm 就是“高”，否则就是“矮”，其余 feature 定义类似。假如每种特征都有两种情况，并且最后的属性“帅/不帅”也有两种，那么计算联合概率分布时，会有 种组合。

如果用数学语言表达就是：

1. 的可能取值有 个，组合数就是
2. 的可能取值有 K 个
3. 总的组合数就是

惊人的组合数，随着指数级的增加而递增。

因此，在朴素贝叶斯法中，需要加了一个特征相互独立的假设，不然我们计算不出来这么大的联合概率分布，这样就可以转化为简单的形式：

• 其中 n 是 的维度

于是，后验概率就是：

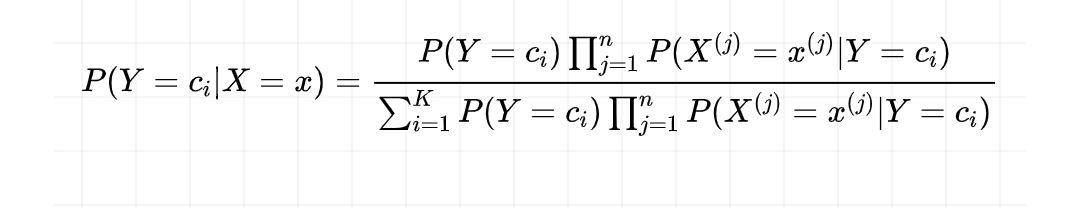
2.3 后验概率最大化的含义

了解了朴素贝叶斯法的重要性，那么我们再来看看它的具体计算方法是什么？

假如存在 K 类 ，现在给定一个新的实例 ，问：该实例归属于哪一类？

现在这个问题对我们来说并不陌生，在前面已经给出了答案：

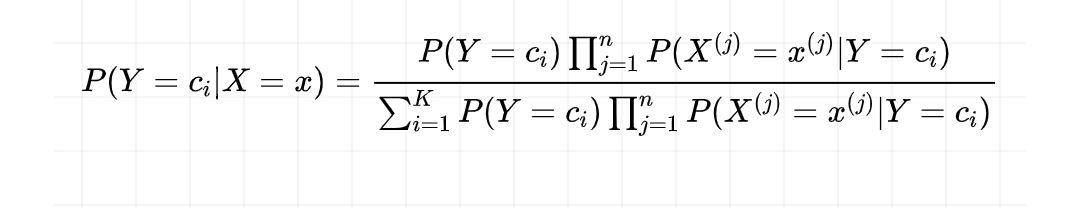
由于分母都相同，因此只要计算出分子的最大值就可找出这个实例所对应的类：

那么对应的判断准则又怎么界定呢？如果得到模型有多个，哪个模型更好呢，如何进行比较？在 k 近邻法中，为了制定规则来决定这个分类函数的好与坏，我们需要比较分类问题的损失情况，在朴素贝叶斯方法中继续用到 0-1 损失函数：

• 是分类决策函数， 是对应的分类，输出空间为

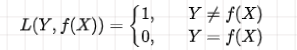
• 当两者相等，证明分类正确，没有损失，反之记为1，有损失。

这个损失函数对应的期望是：

由于朴素贝叶斯法用到的是条件概率的方式，因此对于损失函数的期望也以条件概率进行表达，将损失函数对应的期望最小值可以写成：

期望的下标 ，表示这里的期望对应的是已知 X 下 Y 的条件概率分布。根据数学期望的定义，上面这个期望最小值表达式，就可以理解为是先计算出每个分类的损失函数 乘以对应这个分类发生的概率 ，再对所有计算值进行求和后的结果。

根据这个思路，我们就可以考虑所有的特征后，进行期望最小值的计算，最小的期望风险所对应的那个模型就是我们想要的那一个。

如果，这时候有一个新的实例 ，我们如何得到它的分类决策函数 呢？仍然去找使损失期望最小值的那个！于是当 固定后，根据之前的式子 最小化期望风险就可以写成如下的形式：

而我们知道当 时，损失记为 1，反之为 0，也就意味着只有当 时才会有损失值，否则都为 0，这样就可以对这个函数进行简化：

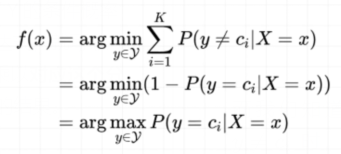
因此上式中的第三行等式去掉了求和符号，意味着对 计算后，找到其中的最大值，记为 ，此时所得到的 就是通过朴素贝叶斯法求出的类。

至此，就实现了将期望风险最小化转为后验概率最大化，这就是朴素贝叶斯法的判断准则，证明了后验概率最大化就是等价于期望风险最小化。

上面如果没看懂，可以看下面这个证明：

点击查看

2.4​ ⭐️ ​朴素贝叶斯分类法的算法

在通过朴素贝叶斯分类法寻找 x 的类别 y 时，可以通过后验概率最大化来实现：

在这个公式里，包含了 n+1 个参数（n 个条件概率和 1 个先验概率），要计算这些参数，我们需要通过训练集来估计，也就是根据样本来推断总体。

计算过程分成三步：

🎵 ​step 1：求出先验概率

这个公式含义是：目标是计算出 的概率， 代表的是第 类，简单来说，就是掰着手指头数一数训练样本集中 类的样本有多少个，然后除以样本总数 N。

🎵 step 2：求出一系列的条件概率

• 表示 有 种可能的取值

这个公式的含义是：计算出某一特征在某一类条件下的概率。一句话总结这个表达式计算的过程：分子是在这个类里对应特征的样本个数，分母是这个类里面的样本总数。

注意，上面两步的概率就是我们得到的 n+1 个参数的估计值，接下来我们计算后验概率。

🎵 step 3：把各类的先验概率和条件概率连乘，得出计算结果最大值，就是对应的类

2.5 例子

有 A、B 两盒巧克力，所在的两个盒子当做两个类，颜色作为巧克力的 feature。如果实例点 x 为黑色巧克力，想要得出它所属的类别，也就是看看是属于 A 盒还是 B 盒，按照朴素贝叶斯分类算法，计算如下：

【step 1】：每个类别的先验概率：

【step 2】：条件概率：

【step 3】：后验概率：

第三步中很明显，来自 A 盒的概率大，因此 ，即黑色巧克力属于 A 盒。

3. 朴素贝叶斯法的参数估计

3.1 极大似然估计的原理

那么极大似然法和朴素贝叶斯的关系是什么呢？没错，它们的思路都是五个字，「概率最大化」。

原理：使似然函数（即联合密度函数）达到最大的参数值。

• 假设 的密度函数为 ，这里 是密度函数的参数值。如果简单随机样本 相互独立，则其联合密度函数为：

• 当 取定值 时， 是 的函数，即样本的似然函数。
• 的极大似然估计 有：

• 记似然函数

3.2 极大似然估计下的 naive Bayes 算法

朴素贝叶斯分类法的算法 中估计先验概率 和条件概率 的计算方法就是用的极大似然估计，算法就是那一节说的。

3.3 ⭐️ ​贝叶斯估计下的 naive Bayes 算法

那么既然有了极大似然估计，为什么还要讲贝叶斯估计呢？因为用极大似然估计可能会出现所要估计的概率值为 0 的情况，这时会影响后验概率的计算结果，使分类产生误差。我们举个例子，你就知道啦。如果我们想要「调查女性占总人口的比例」，而训练数据集选择的是「女儿国」，通过极大似然估计，得出的比例是100%，但是这不能说明总人口只有女性没有男性呀，因此需要用「贝叶斯估计」来解决这个问题。

为了避免用极大似然法计算出的概率值为 0 的情况，贝叶斯估计在「先验概率」和「条件概率」的分子和分母上均引入了一个 ，当 时就是极大似然估计。

先验概率的贝叶斯估计：

贝叶斯估计常取 ，也称为拉普拉斯平滑。

条件概率的贝叶斯估计：

注意，条件概率分母上加的是 ，这是指第 j 个特征中包含的取值个数。比如 为例，它的取值有 ，因此这里的 。