1. 初识感知机

在前面，我们知道学习方法的三要素为模型、策略、算法。这一节，我们就讲一下感知机的模型以及相应的策略。

1.1 Perceptron 简介

感知机是一个二分类的线性分类模型，之所以说是线性，是因为它的模型是线性形式的。

1.1.1 概念

下面我们分别从输入空间、输出空间、模型结构、参数空间和假设空间来看一下感知机：

Input：

• input space：
• input：

Output：

• output space：
• output：

output 代表实例 x 所对应的类别，+1 代表正类，-1 代表负类。

现在我们定义一个从 input space 到 output space 的函数，这个函数就称作 perceptron：

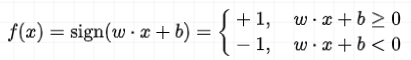
其中 称为 weight， 称为 bias， 表示内积运算。

特征空间里面所有可能的这种线性函数就称为假设空间：。

参数 和 的所有组合，就得到了一个 维的空间，也就是参数空间：。

1.1.2 几何含义

下面我们从几何角度来解释一下感知器。

刚刚那个线性方程 代表着 n 维 feature space 里面的一个 hyperplane ， 是法向量，垂直于 hyperplane， 是相应的截距项。如下图所示：

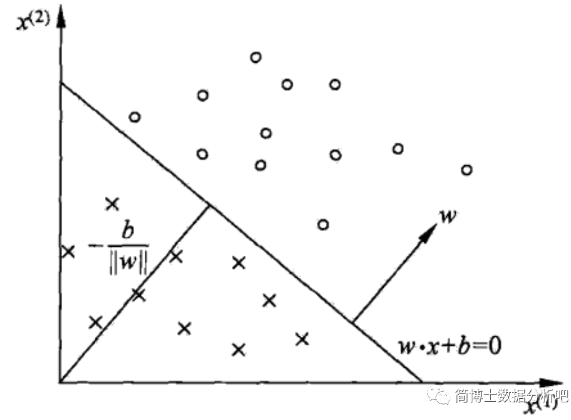
通过 hyperplane 我们就可以将整个特征空间分为两部分，一部分是正类，其中的实例所对应的输出为 +1，一部分为负类，它里面的实例所对应的输出为 -1。所以这个超平面被称为分离超平面。

补充一下 hyperplane 的含义，在几何中，如果环境空间是 n 维的，那么它所对应的 hyperplane 其实就是一个 n-1 维的子空间。换句话说，hyperplane 是比它所处的环境空间小一个维度的子空间。

1.2 学习策略

再来看 perceptron 的第二个要素：学习策略。

perceptron 有一个比较严苛的条件，就是要求数据集必须是线性可分的。什么是线性可分：

通俗的说，对于给定的数据集，如果存在某个 hyperplane，使得这个数据集的所有实例点可以完全划分到hyperplane 的两侧，也就是正类和负类，我们就称这个数据集是线性可分的，否则线性不可分。

如果想要找到能够分开数据集的 hyperplane，就需要确定 model 的 params，这就需要制定一定的学习策略。换而言之，就是要合理地定义感知机相应的损失函数。

首先，我们给出 feature space 中任意一点到 hyperplane 的距离：

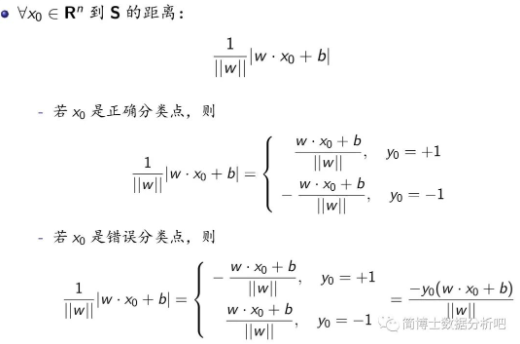
现在我们要关注的就是这里的错误分类点。错误分类点 到 的距离是：，那如果用 M 代表所有误分类点的集合，那我们可以写出所有误分类点到超平面 的距离总和：

很明显，M 中所含有的误分类点越少的时候，总距离和应该越小。在没有误分类点时这个距离和应该是 0。所以，我们可以通过最小化总距离和来求得相应的参数。这时候我们可以简化为最小化下面这个损失函数来实现：

这里 不是一个固定的值，损失函数里为什么可以去掉它了？主要考虑两个方面：

• 不会影响距离和的符号，即不影响正值还是负值的判断

• 不会影响感知器算法的最终结果。算法终止条件，是不存在误分类点。这时候 M 为空集，那么误分类点的距离和是否为 0 取决于分子，而不是分母，因此与 的大小无关

2. 优化算法的扛把子之一：梯度下降法

优化算法有很多，最常用的当属梯度下降法和牛顿法。本节先看一下梯度下降法。

2.1 概念与算法

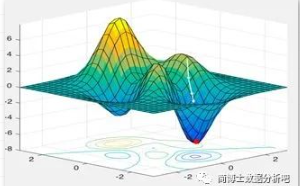
现在，假设有一个可导的函数，我们想找到该函数的极小值，也就是相当于，找一下这座山的山底位置。这个下山过程，对于函数来说就是每次找到该定点相应的梯度，然后沿着梯度的反方向往下走，这就是使函数值下降最快的方向了。

梯度既有方向又有大小，是个矢量。梯度指某一函数在该点处最大的方向导数，沿着该方向可取得最大的变化率：

可见，梯度的方向就是函数在该点处最陡的方向，大小就是在该方向取得的最大变化率，这里最大的变化率也可以称作梯度的模。

下面就是看看如何利用梯度下山。若 是凸函数，我们可以借助梯度下降法求解极小值点，每一步确定方向和步长，更新参数：

这是一个迭代公式， 代表第 k 次所处的位置， 代表步长，更新之后，就到了第 k+1 次所处的位置 。

假如终止条件为 ，接下来迭代计算即可，什么时候到达终止条件，我们就停止迭代，否则，继续循环更新。

这里的 代表范数，本期内容计算对象都是一个数值，所以取的是 L1 范数，如果计算对象是向量，不妨取 L2 范数代表距离，也可以取 范数，代表取最大值。

下面我们给出梯度下降法的详细算法：

上述算法终止条件的含义是，两次迭代所得函数值十分接近，就说明参数已收敛到函数极小值处了。这里的终止条件也可以换成其他的，只要合理即可。

2.2 最速下降法

// TODO

3. 感知机算法 - 原始形式

感知机的算法，通常来说有两种，一个是原始形式的，一个是对偶形式的，本节我们聚焦到原始形式的算法上。

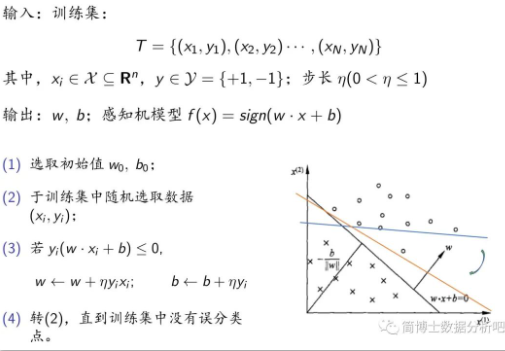
学习的问题表述如下：

如何求参数 和 呢？这就是一个优化问题，寻找使损失函数最小的参数。

这里我们选取随机梯度下降法进行迭代优化计算（注意每次是选取一个误分类点）：

现在我们表述一下训练过程：

4. 感知机算法 - 对偶形式

4.1 算法介绍

在之前讲解的原始形式的学习算法中，如果实例点 是误分类点，可以用它更新参数，即：

假如，每一个实例点对于参数更新做了 次贡献，那么每个实例点作用到初始参数 上的增量分别为 和 ，其中 。特别地，如果取初始参数向量为零向量，那么最终学习到的参数就是：

我们用一个例子来解释：

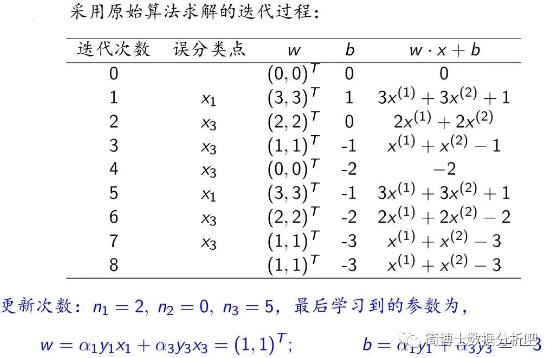
在这个过程中，实例 作为误分类点出现两次，所以 ，即第一个实例点在迭代中贡献了 2 次，又因 ，所以 。其余类似。最终可以计算出 和 。

对偶形式，基本思想就是通过实例点的线性组合来更新参数，其权重由贡献的大小决定。

以下是对偶形式的具体步骤：

可以看到，与原始形式相比，对偶形式的算法在更新步骤中更新的是 而不是 ，这时因为最终的 是可以通过 来计算得到。

与原始形式相比，对偶形式有什么优势呢？这需要，仔细分析对偶形式的迭代条件：

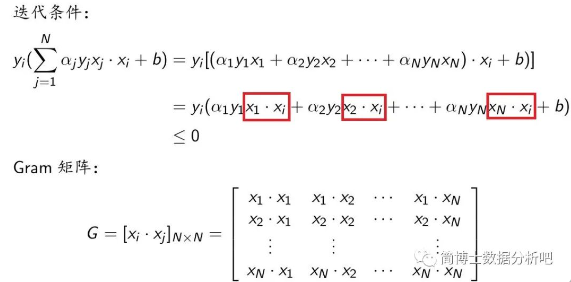
将迭代条件展开，我们发现，如果训练数据集固定，那么有些值是不需要重复计算的，也就是我们红框里的这 N 个内积。在有了 Gram 矩阵后，如果 是误分类点，那么只要读取 Gram 矩阵的第 i 行的值即可。

我们要做的，就是在得到训练数据集之后，把这 个内积计算出来储存到 Gram 矩阵，之后每次更新参数的时候读取就可以，这能节省许多计算量。

4.2 例题解说

例题如下：

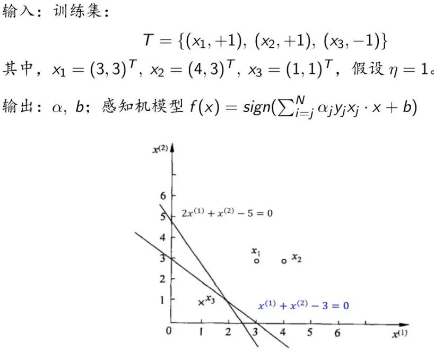
我们看看用对偶算法怎么找到分离超平面：

先设置初始值，不妨还是取零向量，然后计算 Gram 矩阵，把 9 个内积的值都储存下来。接下来就是判断误分类点，可以选取 带入迭代条件中，计算得到零，说明这是一个误分类点，可以用来更新参数。然后再下一轮迭代，寻找一个误分类点：

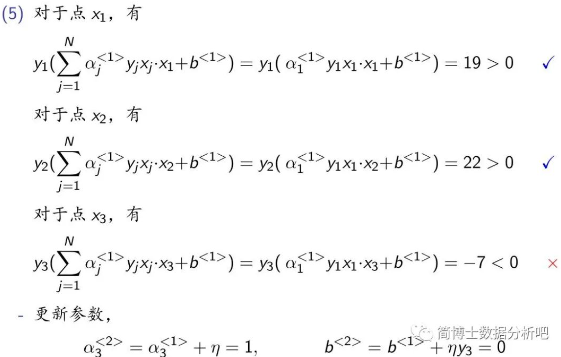
可以计算出 是误分类点，将其用于更新参数。不停重复：

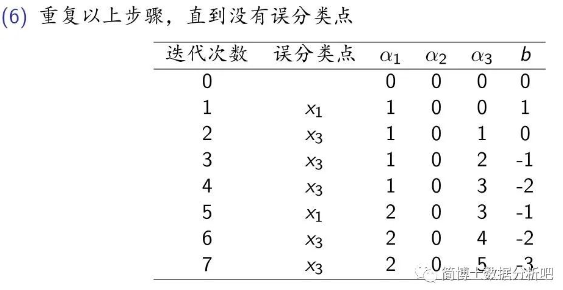
注意每轮是更新 和 ，而不是像原始形式那样更新 和 。

之后，重复步骤，直到没有误分类点，停止迭代，这样，就得到最终模型了。用之前更新后的 可以计算出 ：

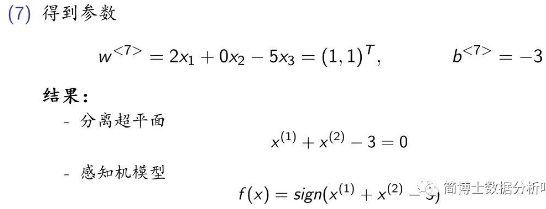
可以看出，无论是原始形式还是对偶形式，如果迭代的过程是一样的，最后得到的分离超平面还有感知机模型是相同的。同样的，类似于原始形式的学习算法，对偶形式的学习算法也是收敛的，而且存在多种解。如果要得到唯一解，需要加约束条件，这就是支持向量机中的内容了。

5. 算法的收敛性证明

// TODO