notebook
yubin
2022-03-31
目录

Gated RNN

上一章的 RNN 存在环路，可以记忆过去的信息，但这个 RNN 的效果并不好。原因在于，许多情况下它都无法很好地学习到时序数据的长期依赖关系。目前简单的 RNN 经常被名为 LSTM 或 GRU 的层所代替。实际上，当我们说 RNN 时，更多的是指 LSTM 层。

LSTM 和 GRU 中增加了一种名为“门”的结构。基于这个门，可以学习到时序数据的长期依赖关系。我们将介绍代替它的 LSTM 和 GRU 等“Gated RNN”，研究 LSTM 的结构并揭示它实现“长期记忆”的机制。

# 1. RNN 的问题

我们举一个例子来说明为什么 RNN 层不擅长长期记忆。

复习 RNN：当输入时序数据 时，RNN 层输出 。这个 也称为 RNN 层的隐藏状态，它记录过去的信息。RNN 利用了上一时刻的隐藏状态来实现继承过去的信息，其计算图为：

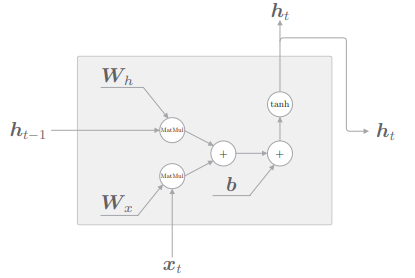
image-20220331220412796

RNN 层的正向传播进行的计算由矩阵乘积、矩阵加法和基于激活函数 tanh 的变换构成，我们来看一下这个 RNN 层存在的问题。

# 1.1 梯度消失和梯度爆炸

语言模型的任务是根据已经出现的单词预测下一个将要出现的单词。在 RNNLM 模型中如果要完成下面这个任务：

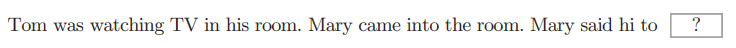
image-20220331221027963

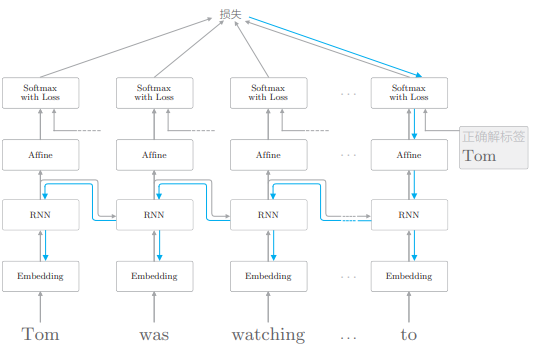
此处应填的是 Tom，而要正确回答这个问题，RNNLM 需要记住前面的两个句子的信息，这些信息必须被编码保存在 RNN 层的隐藏状态中。当我们使用 BPTT 进行学习时，梯度将从正确解标签 Tom 出现的地方向过去的方向传播：

image-20220331221232874

RNN 层通过向过去传递“有意义的梯度”，能够学习时间方向上的依赖关系。但如果这个梯度在中途变弱（甚至没有包含任何信息），则权重参数将不会被更新。不幸的是，随着时间的回溯，这个简单 RNN 未能避免梯度变小（梯度消失）或者梯度变大（梯度爆炸）的命运，因此其无法学习长期的依赖关系。

# 1.2 梯度消失和梯度爆炸的原因

我们深挖一下 RNN 层中梯度消失（或者梯度爆炸）的起因。如下图，这里仅关注 RNN 层在时间方向上的梯度传播：

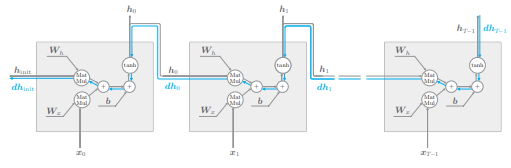
image-20220331221609240

考虑第 T 个正确解标签是 Tom 的情形，此时关注时间方向上的梯度，可知反向传播的梯度流经 tanh、“+”和 MatMul（矩阵乘积）运算。

“+”的反向传播将上游传来的梯度原样传给下游，因此梯度的值不变。而 的导数是 ，其值的变化如图：

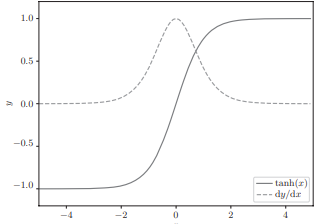
image-20220331222018922

可以看出，当它的值小于 1.0，并且随着 x 远离 0，它的值在变小，这意味着如果经过 tanh 函数 T 次，则梯度也会减小 T 次。

RNN 的激活函数一般使用 tanh 函数，但是如果改为 ReLU 函数，则有希望抑制梯度消失的问题，这是因为在 ReLU 的情况下，当 x 大于 0 时，反向传播将上游的梯度原样传递到下游，梯度不会“退化”。

下面我们关注 MatMul（矩阵乘积）节点，忽略其他节点，这样 RNN 层的反向传播的梯度就仅取决于 MatMul 运算：

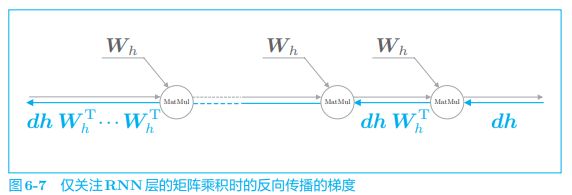
image-20220331222352326
  • 假定从上游传来梯度 ，此时 MatMul 节点的反向传播通过矩阵乘积 计算梯度，之后，根据时序数据的时间步长，将这个计算重复相应次数。这里需要注意的是，每一次矩阵乘积计算都使用相同的权重 。

那么，反向传播时梯度的值通过 MatMul 节点时会如何变化呢？实验后可以看出结果：

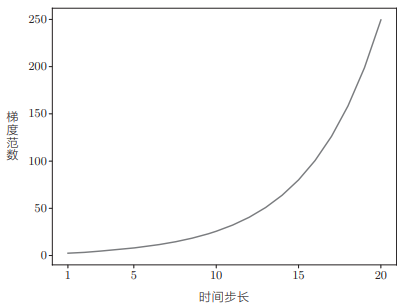
image-20220331222848415

可知梯度的大小随着时间步长呈指数级增加，这就是梯度爆炸。如果发生梯度爆炸，最终就会导致溢出，出现 NaN 之类的值。如此一来，神经网络的学习将无法正确运行。

修改一下初始值，可以看到如下结果：

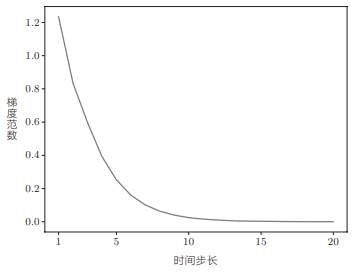
image-20220331223026721

可以看到这次梯度呈指数级减小，这就是梯度消失。如果发生梯度消失，梯度将迅速变小。一旦梯度变小，权重梯度不能被更新，模型就会无法学习长期的依赖关系。

为什么会出现梯度的大小或者呈指数级增加，或者呈指数级减小？因为矩阵 被反复乘了 T 次。如果 是标量，这很容易理解。而如果 是矩阵的话，矩阵的奇异值将成为指标。简单而言，矩阵的奇异值表示数据的离散程度。根据这个奇异值（更准确地说是多个奇异值中的最大值）是否大于 1，可以预测梯度大小的变化。

如果奇异值的最大值大于 1，则可以预测梯度很有可能会呈指数级增加；而如果奇异值的最大值小于 1，则可以判断梯度会呈指数级减小。但并不是说奇异值比 1 大就一定会出现梯度爆炸。这是必要条件，而不是充分条件。

# 1.3 梯度爆炸的对策

解决梯度爆炸有既定的方法，称为梯度裁剪（gradients clipping），其伪代码为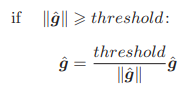：image-20220331223522862

  • 假设可以将神经网络用到的所有参数的梯度整合成一个，并用符号 表示。
  • 将阈值设置为 threshold。此时，如果梯度的 L2 范数 大于或等于阈值，就按上述方法修正梯度，这就是梯度裁剪。

虽然这个方法很简单，但是在许多情况下效果都不错。

我们用 Python 来实现一下梯度裁剪：

import numpy as np

dW1 = np.random.rand(3, 3) * 10
dW2 = np.random.rand(3, 3) * 10
grads = [dW1, dW2]  # 梯度的列表
max_norm = 5.0      # 阈值

def clip_grads(grads, max_norm):
	total_norm = 0
	for grad in grads:
		total_norm += np.sum(grad ** 2)
	total_norm = np.sqrt(total_norm)
    
	rate = max_norm / (total_norm + 1e-6)
	if rate < 1:
		for grad in grads:
            grad *= rate

clip_grads(grads, max_norm)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

我们在用于 RNNLM 学习的 RnnlmTrainer 类的内部利用了上述梯度裁剪以防止梯度爆炸。

以上是对梯度裁剪的说明，用于解决梯度爆炸的问题。下面，我们看一下防止梯度消失的对策。

# 2. 梯度消失和 LSTM

梯度消失也是一个大问题，为了解决它，需要从根本上改变 RNN 层的结构，这里本章的主题 Gated RNN 就要登场了。人们提出了很多 Gated RNN 结构，其中 LSTM 和 GRU 比较具有代表性，我们将关注 LSTM 并仔细研究它的结构，并阐明为何它不会（难以）引起梯度消失。

# 2.1 LSTM 的接口

为了方便，我们在计算图中引入“简略图示法”，它将矩阵计算等整理为一个长方形节点：

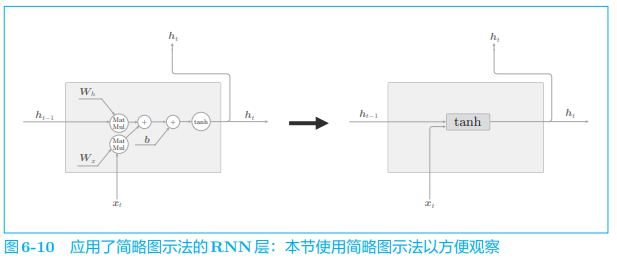
image-20220401082847850

  • 这里将 这个计算表示为一个长方形节点 。

我们来比较一下 RNN 层和 LSTM 层：

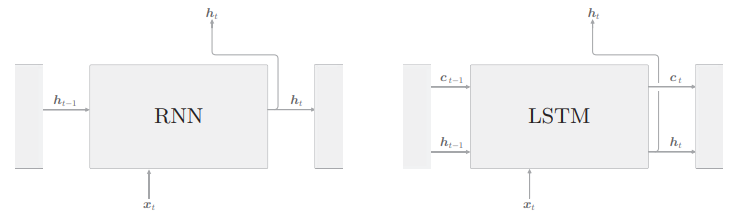
image-20220401083251751

不同之处在于 LSTM 还有路径 ，称为记忆单元（简称“单元”），相当于 LSTM 专用的记忆部门。记忆单元的特点是仅在 LSTM 层内部接收和传递数据，在内部结束工作后不向其它层输出。而 LSTM 的隐藏状态 和 RNN 层相同，会被（向上）输出到其他层。

从接收LSTM的输出的一侧来看，LSTM 的输出仅有隐藏状态向量 h。记忆单元 c 对外部不可见，我们甚至不用考虑它的存在。

# 2.2 LSTM 层的结构

我们一个一个地组装 LSTM 的部件，并仔细研究他们的结构。

LSTM 的记忆单元 存储了时刻 t 时 LSTM 的记忆，可以认为其中保存了从过去到时刻 t 的所有必要信息，然后基于这些记忆来向外部的层（和下一时刻的 LSTM）输出隐藏状态 ：

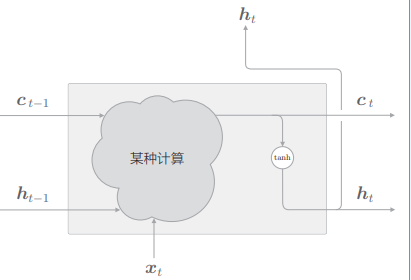
image-20220401084346124
  • 当前的记忆单元 是基于 3 个输入 、 和 ，经过“某种计算”算出来的。
  • 这里的重点是隐藏状态 要使用更新后的 来计算，这个计算是 ，表示对 的逐元素应用 函数。

我们再来说一下 Gate 的功能。Gate 就像门打开或合上一样，控制数据的流动。直观上，门的作用就是阻止或者释放水流。如下图，可以将“开合程度”控制在 0.7 或者 0.2：

image-20220401085615848

门的开合程度由 0.0 ~1.0 的实数表示（1.0 表示全开），通过这个数值控制流出的水量。这里的重点是，门的开合程度也是（自动）从数据中学习到的。

有专门的权重参数用于控制门的开合程度，这些权重参数通过学习被更新。另外，sigmoid 函数用于求门的开合程度（sigmoid 函数的输出范围在 0.0 ~ 1.0）。

# 2.3 输出门

刚刚计算隐藏状态 仅仅是对记忆单元 应用了 函数，现在考虑对 施加门，从而针对 的各个元素，调整它们作为下一时刻的隐藏状态的重要程度。由于这个门管理下一个隐藏状态 的输出，所以称为输出门（output gate）。

输出门的开合程度 计算式如下：

  • 它根据输入 和上一个状态 求出
  • 这里使用的权重参数和偏置的上标添加了 output 的首字母 o，之后我们也将使用上标表示门
  • 另外 sigmoid 函数用 表示

计算得到的开合程度 会与 的对应元素做乘积，作为 输出，绘制成计算图如下：

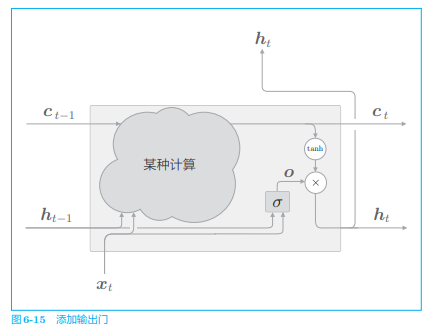
image-20220401095806232
  • 即 sigmoid 运算，其输出就是开合程度
  • 由 和 的阿达玛乘积（即对应元素的乘积，用 表示）：

的输出是 −1.0 ~ 1.0 的实数。我们可以认为这个 −1.0 ~ 1.0 的数值表示某种被编码的“信息”的强弱（程度）。而 sigmoid 函数的输出是 0.0~1.0 的实数，表示数据流出的比例。因此，在大多数情况下，门使用 sigmoid 函数作为激活函数，而包含实质信息的数据则使用 函数作为激活函数。

如此，LSTM 的输出部分就完成了，接着我们看一下记忆单元的更新部分。

# 2.4 遗忘门

只有放下包袱，才能轻装上路。接下来，我们要做的就是明确告诉记忆单元需要“忘记什么”。

现在，我们在记忆单元 上添加一个忘记不必要记忆的门，这里称为遗忘门（forget gate）。遗忘门进行的计算也表示为 ，其中有遗忘门专用的权重参数，其输出 的计算如下：

然后， 由这个 和上一个记忆单元 的对应元素的乘积求得：

此时计算图绘制如下：

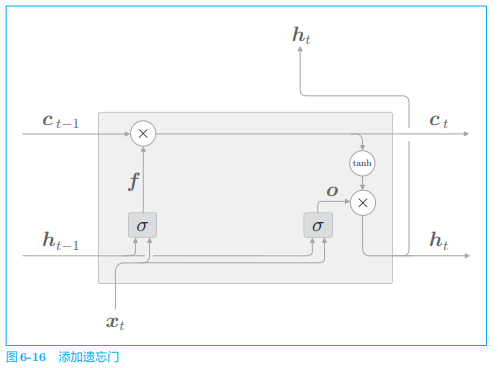
image-20220401111139487
  • 左边的 是遗忘门，右边的是输出门

# 2.5 新的记忆单元

遗忘门从上一时刻的记忆单元中删除了应该忘记的东西，现在我们还想向这个记忆单元添加一些应当记住的新信息，为此我们添加新的 节点：

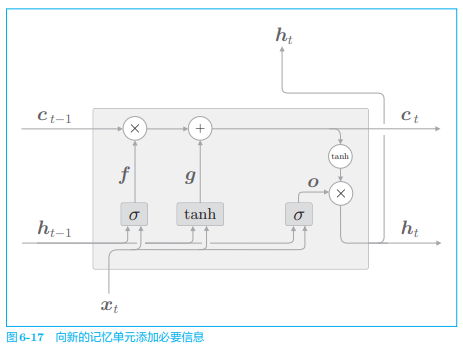
image-20220401111400956

如图所示，基于 节点计算出的结果被加到上一时刻的记忆单元 上，这样一来，新的信息 就被添加到了记忆单元中。这个 节点的作用不是门，而是将新的信息添加到记忆单元中，因此它不用 sigmoid 作为激活函数，而是使用 函数，此节点处的计算如下：

  • 表示向记忆单元添加的新信息

# 2.6 输入门

最后，我们向上一节的图 6-17 的 添加一个输入门（input gate），输入门判断新增信息 g 的各个元素的价值有多大。输入门不会不经考虑就添加新信息，而是会对要添加的信息进行取舍，换句话说，输入门会添加加权后的新信息：

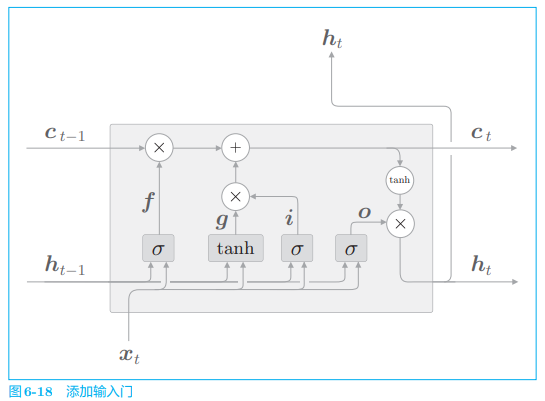
image-20220401143019234

用 表示输入门，用 表示输入门的输出，此时进行的计算如下：

然后将 和 的对应元素的乘积添加到记忆单元中。以上就是对 LSTM 内部处理的说明。

LSTM 有许多变体，这里说明的是最具有代表性的，其他也有许多在门的连接方式上稍微不同的其他 LSTM。

# 2.7 LSTM 的梯度的流动

为什么刚刚介绍的 LSTM 不会引起梯度消失呢？其原因可以通过观察记忆单元 的反向传播来了解:

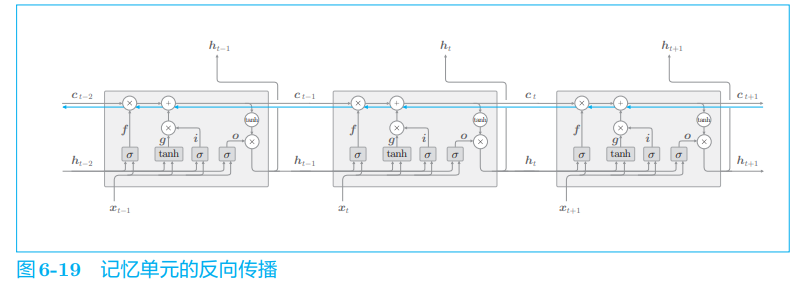
image-20220401145747390

我们仅关注记忆单元，绘制了它的反向传播，此时，记忆单元的反向传播仅流过“+”和“×”节点。“+”节点将上游传来的梯度原样流出，所以梯度没有退化，而“×”节点的计算并不是矩阵乘积，而是对应元素的乘积，而且每次都会基于不同的门值进行对应元素的乘积计算。这就是它不会发生梯度消失（或梯度爆炸）的原因。

之前简单的 RNN 是由于使用相同的权重矩阵重复了多次矩阵乘积才导致的梯度消失或梯度爆炸。

“×”节点的计算由遗忘门控制，它认为“应该忘记”的记忆单元的元素，其梯度会变小；而遗忘门认为“不能忘记”的元素，其梯度在向过去的方向流动时不会退化。因此，可以期待记忆单元的梯度（应该长期记住的信息）能在不发生梯度消失的情况下传播，从而能够学习长期的依赖关系。

LSTM 是 Long Short-Term Memory（长短期记忆）的缩写，意思是可以长（Long）时间维持短期记忆（Short-Term Memory）。

# 3. LSTM 的实现

# 3.1 LSTM 类

我们将进行单步处理的类实现为 LSTM 类，将整体处理 T 步的类实现为 TimeLSTM 类。

LSTM 中进行的计算有：image-20220401150358746

注意 (6,6) 中的 4 个仿射变换的式子，即 这样的式子。这四个式子可以整合为一个式子进行：

image-20220401150615407

这样计算图可以绘制成下图：

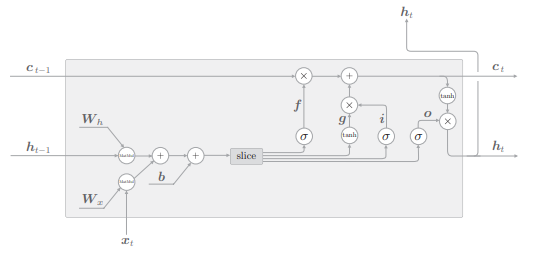
image-20220401151531119
  • 先执行 4 个仿射变换，然后由 slice 节点均等的分成四份并去除相应的内容，然后再流入激活函数进行之前所介绍的计算。

对计算做形状检查：

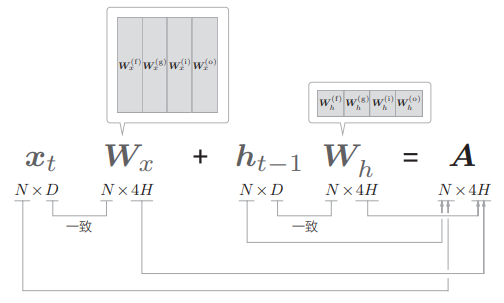
image-20220401151724927
  • 批大小是 N，输入数据的维数是 D，记忆单元和隐藏状态的维数都是 H

反向传播的实现也不困难，这里特别说一下 slice 节点的反向传播：

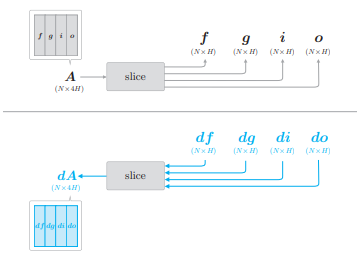
image-20220401151936889

  • 可以用代码：dA = np.hstack((df, dg, di, do)) 来完成。

具体的代码实现就不详细介绍了。

# 3.2 TimeLSTM 类

Time LSTM 层是整体处理 T 个时序数据的层，由 T 个 LSTM 层构成：

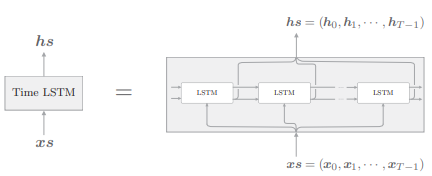
image-20220401152733029

Truncated BPTT 以适当的长度截断反向传播的连接，但是需要维持正向传播的数据流。为此，将隐藏状态和记忆单元保存在成员变量中，以便在调用下一个 forward 函数时可以继承上一个时刻的隐藏状态（和记忆单元）：

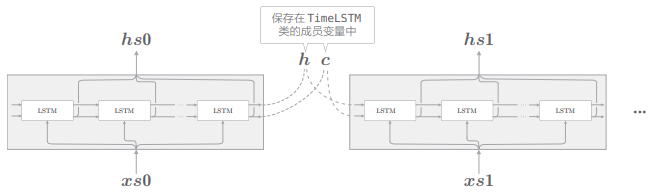
image-20220401153507577

TimeLSTM 类的实现和 TimeRNN 类几乎一样，且仍通过参数 stateful 指定是否维持状态。

# 4. 使用 LSTM 的语言模型

现在我们来实现语言模型，这里实现的语言模型和上一章几乎是一样的，唯一的区别是，上一章使用 Time RNN 层的地方这次使用 Time LSTM 层：

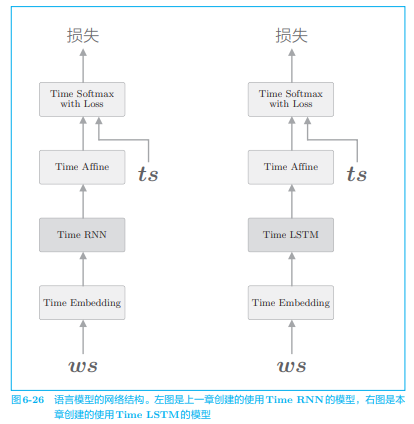
image-20220401153821259

我们下面在 PTB 数据集上学习这个网络，这次我们使用 PTB 数据集的所有训练数据来进行学习。我们来看一下训练结果的困惑度的演变图：

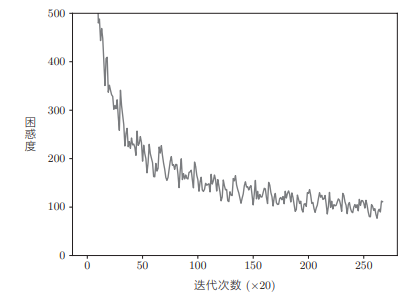
image-20220401154030839

在这次的实验中，一共进行了 4 个 epoch 的学习，困惑度顺利下降，最终达到 100 左右。基于最终的测试数据的评价结果为 136.07。该结果在每次执行时都不相同，但是都在 135 前后。换句话说，我们的模型成长到了能将下一个单词的候选个数（从 10 000 个）缩小到 136 个左右的水平。

说实话，这并不是一个很好的结果。在 2017 年的一个研究中，PTB 数据集上的困惑度已经降到了 60 以下。我们的模型还有很大的改进空间，下面我们就来进一步改进现有的 RNNLM。

# 5. 进一步改进 RNNLM

本节我们先针对当前的 RNNLM 说明 3 点需要改进的地方。

# 5.1 LSTM 层的多层化

在使用 RNNLM 创建高精度模型时，加深 LSTM 层（叠加多个 LSTM 层）的方法往往很有效。通过叠加多个层，可以提高语言模型的精度。

下面的网络使用了两个 LSTM 层：

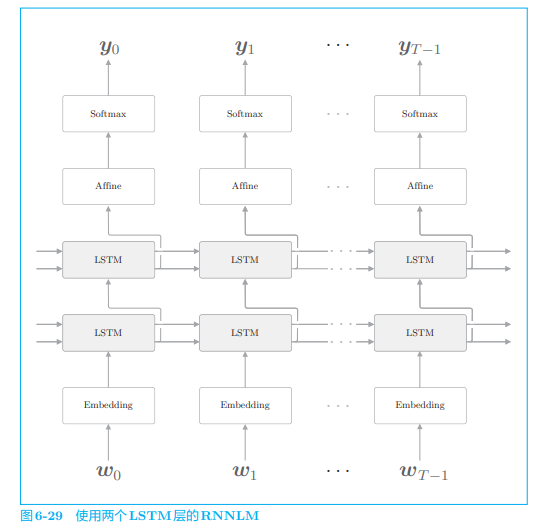
image-20220401154427454

在叠加两个 LSTM 层时，第一个 LSTM 层的隐藏状态是第二个 LSTM 层的输入。按照同样的方式，我们可以叠加多个 LSTM 层，从而学习更加复杂的模式。具体应该叠加几个层，就是超参数的问题了。

谷歌翻译中使用的 GNMT 模型是叠加了 8 层 LSTM 的网络。如果待解决的问题很难，又能准备大量的训练数据，就可以通过加深 LSTM 层来提高精度。

# 5.2 基于 Dropout 抑制过拟合

通过加深层，可以创建表现力更强的模型，但是这样的模型往往会发生过拟合，更糟糕的是，RNN 比常规的前馈神经网络更容易发生过拟合，因此 RNN 的过拟合对策非常重要。

抑制过拟合已有既定的方法：一是增加训练数据；二是降低模型的复杂度。除此之外，对模型复杂度给予惩罚的正则化也很有效。此外像 Dropout 这样，在训练时随机忽略一部分神经元，也可以被视为一种正则化。我们就仔细研究 Dropout 并将其用于 RNN。

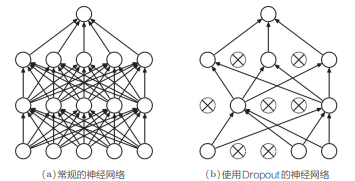
image-20220401155921618

Dropout 随机选择一部分神经元，然后忽略它们，停止向前传递信号。这种“随机忽视”是一种制约，可以提高神经网络的泛化能力。

那么，在使用 RNN 的模型中，应该将 Dropout 层插入哪里呢？首先可以想到插入在 LSTM 层的时序方向上，不过这并不是一个好的插入方式：

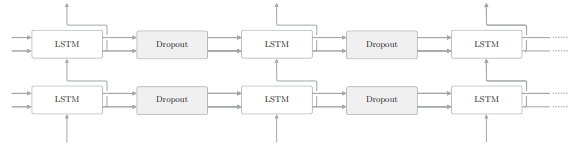
image-20220401160102370

如果在时序方向上插入 Dropout，那么当模型学习时，因 Dropout 产生的噪声会随时间成比例地积累。考虑到噪声的积累，最好不要在时间轴方向上插入 Dropout。因此，我们在深度方向上插入 Dropout 层：

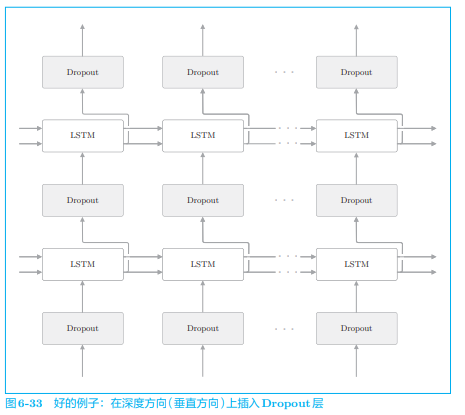
image-20220401161129098

这样一来，无论沿时间方向（水平方向）前进多少，信息都不会丢失。Dropout 与时间轴独立，仅在深度方向（垂直方向）上起作用。

如前所述，“常规的 Dropout”不适合用在时间方向上。但是，最近的研究提出了多种方法来实现时间方向上的 RNN 正则化。“变分 Dropout”（variational dropout）就被成功地应用在了时间 方向上。

据说变分 Dropout 比常规 Dropout 的 效果更好。不过我们之后仍使用常规 Dropout，变分 Dropout 的想法很简单，可以查阅相关资料。

# 5.3 权重共享

改进语言模型有一个非常简单的技巧，那就是权重共享（weight tying）。

weight tying 可以直译为“权重绑定”，但其含义就是共享权重

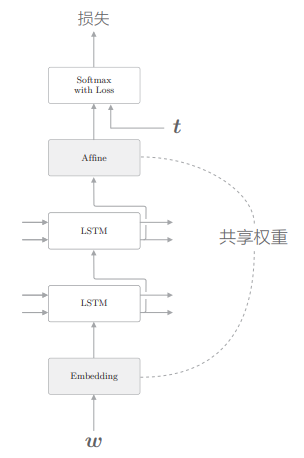
image-20220401173255763

现在，我们来考虑一下权重共享的实现。假设词汇量为 V，LSTM 的隐藏状态的维数为 H，则 Embedding 层的权重形状为 V × H，Affine 层的权重形状为 H × V。此时，如果要使用权重共享，只需将 Embedding 层权重的转置设置为 Affine 层的权重。这个非常简单的技巧可以带来出色的结果。

为什么说权重共享是有效的呢？直观上，共享权重可以减少需要学习的参数数量，从而促进学习。另外，参数数量减少，还能收获抑制过拟合的好处。

# 5.4 更好的 RNNLM 的实现

至此，我们介绍了 RNNLM 的 3 点有待改进的地方。接下来，我们来看一下这些技巧会在多大程度上有效。这里我们将其实现为 BetterRnnlm 类：

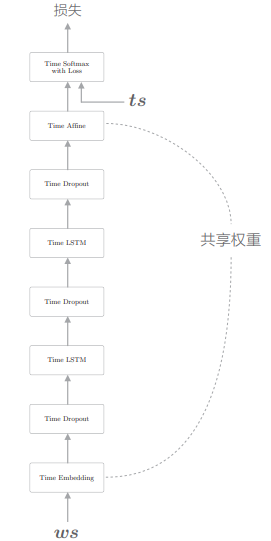
image-20220401193233105

这里做了三点改进：

  • LSTM 层的多层化
  • 使用了 Dropout（仅在深度方向上）
  • 权重共享（Embedding 层和 Affine 层的权重共享）

同时在学习时做一个小改动：针对每个 epoch 使用验证数据评价困惑度，在值变差时，降低学习率。这是一种在实践中经常用到的技巧，并且往往能有好的结果。

执行上面的代码，困惑度平稳下降，最终在测试数据上获得了困惑度为 75.76 的结果（每次运行结果不同），这个结果相比于改进前的 136 可以说提升很大。通过 LSTM 的多层化提高表现力，通过 Dropout 提高泛化能力，通过权重共享有效利用权重，从而实现了精度的大幅提高。

# 5.5 前沿研究

至此，我们对 RNNLM 的改进就结束了。我们得到了不错的效果，但前沿研究走得更远。一个先进的模型使用了多层 LSTM 模型，并进行了基于 Dropout 的正则化（变分 Dropout 和 DropConnectA）和权重共享，在此基础上，它进一步使用了最优化和正则化的几个技巧，并严格进行了超参数的调整，最终达成了 52.8 这样惊人的值。

编辑 (opens new window)
上次更新: 2022/08/26, 13:48:42
RNN
seq2seq

← seq2seq→

最近更新
01
Deep Reinforcement Learning
10-03
02
误删数据后怎么办
04-06
03
MySQL 一主多从
03-22
更多文章>
Theme by Vdoing | Copyright © 2021-2024 yubincloud | MIT License
×