notebook
yubin
2022-03-06
目录

神经网络的复习

本书附带资料可见 深度学习进阶：自然语言处理 (ituring.com.cn) (opens new window)

# 1. 张量

不再介绍向量和矩阵的基础知识。

在数学和深度学习等领域，向量一般作为列向量处理，不过，考虑到实现层面的一致性，本书将向量作为行向量（每次都会注明是行向量），在代码中往往会用 x 或 W 这样来表示向量和矩阵。行向量也可视为 的矩阵。

# 2. 神经网络的推理

神经网络中进行的处理分为学习和推理两部分，本节先介绍推理部分。

# 2.1 神经网络推理过程的全貌

神经网络将输入变换成输出。我们考虑一个输入二维数据，输出三维数据的模型：

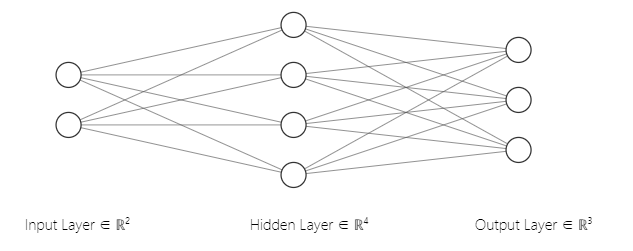
image-20220308161503018

  • 往往用圆圈 ○ 表示神经元，用箭头表示它们的连接。此时，箭头上有权重，这个权重和对应的神经元的值分别相乘，其和（严格地讲，是经过激活函数变换后的值）作为下一个神经元的输入。

上图中网络一共包含三层，但实际有权重的只有两层，所以我们称之为 2 层神经网络，但也有文献称之为 3 层神经网络。

下面用数学式子来表示该网络进行的计算。输入层数据是 ，用 、 表示权重，偏置为 ，这样隐藏层的第 1 个神经元的计算是： 。

这些下标的规则并不重要，实际上，第一层的全连接层的变换通过矩阵乘积表示如下：

  • 可以对矩阵的运算进行形状检查。

形状检查

我们往往会同时将多笔样本数据（称为 mini-batch，小批量）进行推理和学习，因此我们将单独的样本数据保存在矩阵 的各行中。假设 batch size 为 N，即 N 个样本作为一个 mini-batch。

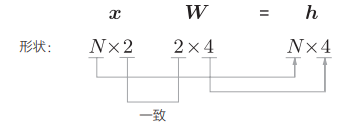
image-20220315221352971

  • 在矩阵乘积等计算中，注意矩阵的形状并观察其变化的形状检查非常重要。据此，神经网络的实现可以更顺利地进行。

全连接是线性变换，激活函数赋予它“非线性”的效果，这里我们使用 sigmoid。

# 2.2 层的类化及正向传播的实现

因为全连接层的变化类似于仿射变换，所以称之为 Affine 层。Sigmoid 的变换称之为 Sigmoid 层。神经网络有各种各样的层，我们将其实现为 Python 的类，通过这种模块化，可以像乐高积木一样搭建网络。在实现它们时，我们制定了如下代码规范：

  • 所有的层都有 forward 方法 和 backward 方法，对应正向和反向传播
  • 所有的层都有 params 和 grads 实例变量，params 使用列表保存权重和偏置等参数，grads 以与 params 对应的方式保存各参数的梯度

这里先只考虑正向传播，因此先把重点放到 forward 和 params 上。

# 2.2.1 sigmoid 层的实现

import numpy as np

class Sigmoid:
    def __init__(self):
        self.params = []

    def forward(self, x):
        return 1 / (1 + np.exp(-x))
1
2
3
4
5
6
7
8
  • 因为 Sigmoid 没有可以学习的参数，所以使用空列表来初始化 params

# 2.2.2 Affine 层的实现

class Affine:
    def __init__(self, W, b):
        self.params = [W, b]

    def forward(self, x):
        W, b = self.params
        out = np.dot(x, W) + b
        return out
1
2
3
4
5
6
7
8
  • 在初始化时接收权重和偏置。

# 2.2.3 搭建一个网络

现在我们使用上面的层来搭建一个如下的网络：

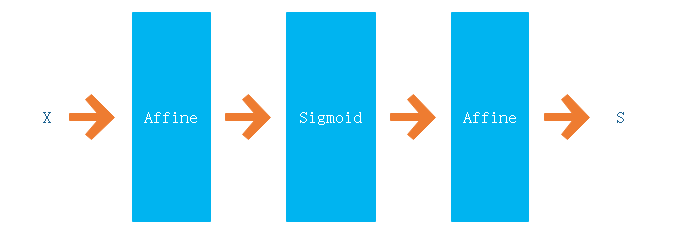
image-20220308164725950 
class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size):
        I, H, O = input_size, hidden_size, output_size

        # 初始化权重和偏置
        W1 = np.random.randn(I, H)
        b1 = np.random.randn(H)
        W2 = np.random.randn(H, O)
        b2 = np.random.randn(O)

        # 生成层
        self.layers = [
            Affine(W1, b1),
            Sigmoid(),
            Affine(W2, b2)
        ]

        # 将所有的权重整理到列表中
        self.params = []
        for layer in self.layers:
            self.params += layer.params

    def predict(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
  • 将推理处理实现为 predict(x) 方法。

# 3. 神经网络的学习

# 3.1 损失函数

基于监督数据和神经网络的预测结果，将模型的恶劣程度作为标量计算出来，得到的就是损失。损失指示学习阶段中某个时间点的神经网络的性能。

进行多类别分类时，常用交叉熵误差（cross entropy error）作为损失函数。这里，我们将 softmax 和 cross entropy error 层加入网络中。

我们将 softmax 与交叉熵误差的层实现为 Softmax with Loss 层，这里省略其说明，代码在 common/layers.py 中。

# 3.1.1 softmax

softmax 函数：

  • 该式是当输出总共有 n 个时，计算第 k 个输出 时的算式，这个 是对应于第 k 个类别的 softmax 函数的输出。

softmax 函数输出的各个元素是 0.0 ～ 1.0 的实数。另外，如果将这些元素的和为 1。因此，softmax 的输出可以解释为概率。之后， 这个概率往往会被输入交叉熵误差。

得分（score）是计算概率之前的值。得分越高，这个神经元对应的类别的概率越高。我们可以把得分输入 softmax 层，得到概率。

# 3.1.2 交叉熵误差

交叉熵误差：

  • 是对应于第 k 个类别的监督标签，它以 one-hot 向量的形式表示，比如 t = (0, 0, 1)。

在考虑了 mini-batch 处理的情况下，交叉熵误差可以表示为：

  • 这里假设数据有 N 笔，下标 表示第 n 笔数据的第 k 维元素的值， 表示神经网络的输出， 表示监督标签。
  • 该式看上去有些复杂，其实只是将表示单笔数据的损失函数的式扩展到了 N 笔数据的情况。除以 N 可以求单笔数据的平均损失。通过这样的平均化，无论 mini-batch 的大小如何，都始终可以获得一致的指标。

引入了 Softmax with Loss 层后的一个神经网络示例：

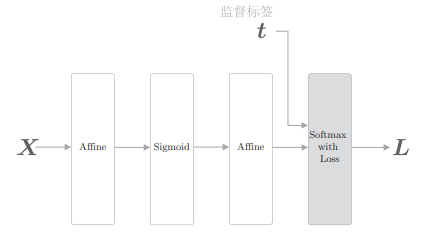
image-20220315223329994

# 3.2 导数和梯度

神经网络的学习目标是找到损失尽可能小的参数。

求导时，假设有函数 ，其中 L 是标量，x 是向量，此时， 关于 的导数可以写成：。即：

矩阵也是类似。这里的重点是，矩阵 和 具有相同的形状。利用“矩阵和其梯度具有相同的形状”这一性质，可以轻松地进行参数的更新和链式法则的实现。

# 3.3 链式法则

两个函数：，那么有 。

链式法则的重要之处在于，无论我们要处理的函数有多复杂（无论复合了多少个函数），都可以根据它们各自的导数来求复合函数的导数。也就是说，只要能够计算各个函数的局部的导数，就能基于它们的积计算最终的整体的导数。

# 3.4 计算图

计算图是计算过程的图形表示。

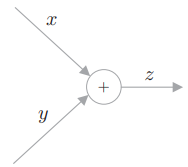
image-20220315223645029
  • 此图便是 的计算图。
  • 计算图通过节点和箭头来表示。变量写在箭头上，用节点表示计算，处理结果有序流动。

这里重要的是，梯度沿与正向传播相反的方向传播，这个反方向的传播称为反向传播。

我们看一下反向传播的全貌。虽然我们处理的是 z = x + y 这 一计算，但是在该计算的前后，还存在其他的“某种计算”。另外， 假设最终输出的是标量 L（在神经网络的学习阶段，计算图的最终输出是损失，它是一个标量）：

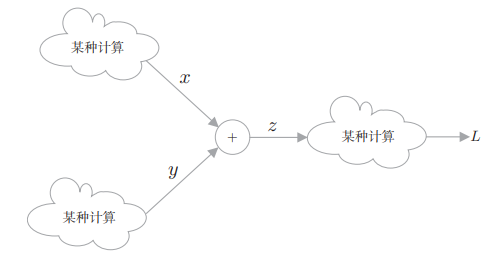
image-20220315224012379

我们的目标是求 L 关于各个变量的导数（梯度）。这样一来，计算图的反向传播就可以绘制成下图：

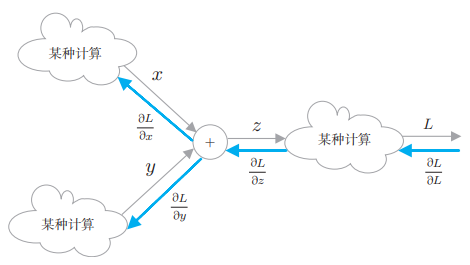
image-20220315224048275
  • 反向传播用蓝色的粗箭头表示，在箭头的下方标注传播的值。此时，传播的值是指最终的输出 L 关于各个变量的导数。

这里我们处理一下 z = x + y 这个节点的运算，，所以加法节点将上游传来 的值乘以 1，再将该梯度向下游传播：

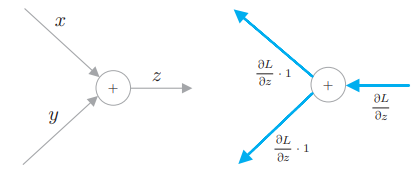
image-20220315224406786

下面，我们将介绍几个典型的运算节点。

# 3.4.1 乘法节点

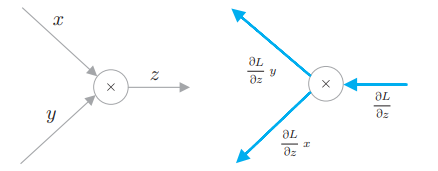
image-20220315224745808

乘法节点的计算是 ，导数可以分别求出 。

可以这样理解：最终的输出是 L，所要求的是 L 关于各个变量的导数，那么 L 关于 x 的导数就是：

在目前为止的加法节点和乘法节点的介绍中，流过节点的数据都是“单变量”。但是，这不仅限于单变量，也可以是多变量。当张量流过加法节点（或者乘法节点）时，只需独立计算张量中的各 个元素。

# 3.4.2 分支节点

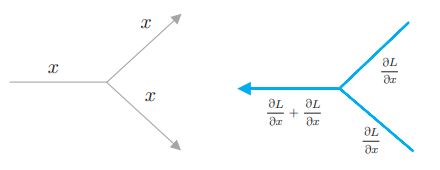
image-20220315225423954

相同的值被复制并分叉。因此，分支节点也称为复制节点。它的反向传播是上游传来的梯度之和。

# 3.4.3 Repeat 节点

分支节点有两个分支，但也可以扩展为 N 个分支（副本），这里称为 Repeat 节点。

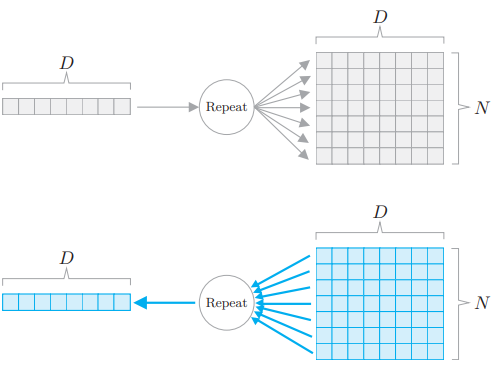
image-20220315225607849

这个例子中将长度为 D 的数组复制了 N 份。因为这个 Repeat 节点可以视为 N 个分支节点，所以它的反向传播可以通过 N 个梯度的总和求出。

示例：

>>> import numpy as np
>>> D, N = 8, 7
>>> x = np.random.randn(1, D) # 输入
>>> y = np.repeat(x, N, axis=0) # 正向传播

>>> dy = np.random.randn(N, D) # 假设的梯度
>>> dx = np.sum(dy, axis=0, keepdims=True) # 反向传播
1
2
3
4
5
6
7
  • 通过指定 keepdims=True，可以维持二维数组的维数。在上面的例子中，当 keepdims=True 时，np.sum() 的结果的形状是 (1, D)；当 keepdims=False 时，形状是 (D, )。

# 3.4.4 Sum 节点

Sum 节点是通用的加法节点。这里考虑对一个 N × D 的数组沿第 0 个轴求和。

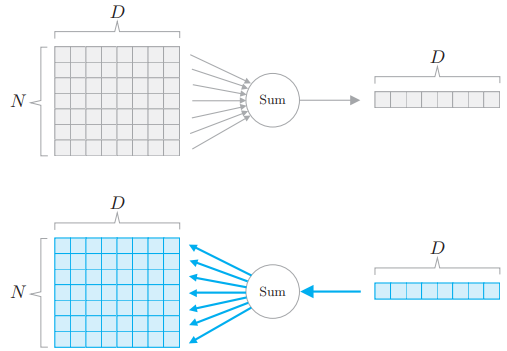
image-20220315225907433
  • shape 为 (N, D) 的矩阵 X，在经过沿第 0 个轴求和后，即 np.sum(X, aixs=0) 后，会使原来 X 的第 0 个轴消失，结果的 shape 变成 (D, )，当设置 keepdims 时则会变成 (1, D)。

Sum 节点的反向传播将上游传来的梯度分配到所有箭头上。这是加法节点的反向传播的自然扩展。示例：

>>> import numpy as np
>>> D, N = 8, 7
>>> x = np.random.randn(N, D) # 输入
>>> y = np.sum(x, axis=0, keepdims=True) # 正向传播

>>> dy = np.random.randn(1, D) # 假设的梯度
>>> dx = np.repeat(dy, N, axis=0) # 反向传播
1
2
3
4
5
6
7

# 3.4.5 MatMul 节点

我们将矩阵乘积称为 MatMul 节点。我们考虑 这个计算：

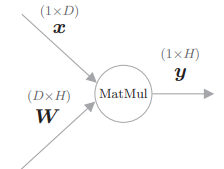
image-20220316141914837

此时可以按如下方式求关于 的第 个元素的导数 ：

  • 表示变化程度，即当 发生微小的变化时，L 会有多大程度的变化。如果此时改变 ，则向量 的所有元素都会发生变化。另外，因为 的各个元素会发生变化，所以最终 也会发生变化。因此，从 到 的链式法则的路径有多个，它们的和是 。

将上式简化，利用 代入得：

由上式可得 由向量 和 的第 i 行向量的内积求得，即：

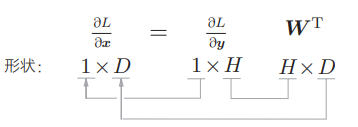
做形状检查：image-20220316143529661

再将它考虑到 mini-batch 处理的情况，假设 中保存了 N 笔数据，反向传播的计算图为：

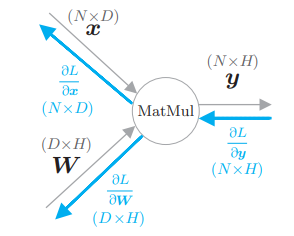
image-20220316143633062

并确认一下矩阵的形状：

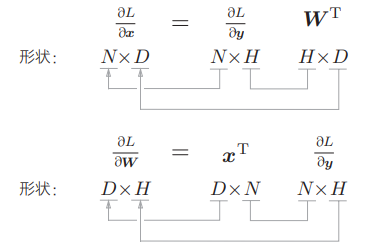
image-20220316143726196

现在我们 将 MatMul 节点实现为层：

class MatMul:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.x = None

    def forward(self, x):
        W, = self.params
        out = np.dot(x, W)
        self.x = x
        return out

    def backward(self, dout):
        W, = self.params
        dx = np.dot(dout, W.T)
        dW = np.dot(self.x.T, dout)
        self.grads[0][...] = dW
        return dx
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 3.5 梯度的推导和反向传播的实现

计算图的介绍结束了，下面我们来实现一些实用的层。这里，我们将实 现 Sigmoid 层、全连接层 Affine 层和 Softmax with Loss 层。

# 3.5.1 Sigmoid 层

Sigmoid 函数为 ，其导数为：：

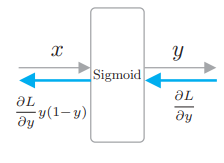
image-20220316144404243

实现为 Sigmoid 层：

class Sigmoid:
    def __init__(self):
        self.params, self.grads = [], []
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        return dx
1
2
3
4
5
6
7
8
9
10
11
12
13
  • 这里将正向传播的输出保存在实例变量 out 中。然后，在反向传播中， 使用这个 out 变量进行计算。

# 3.5.2 Affine 层

我们通过 y = np.dot(x, W) + b 实现了 Affine 层的正向传播。 此时，在偏置的加法中，使用了 NumPy 的广播功能，可将其视为 Repeat 运算：

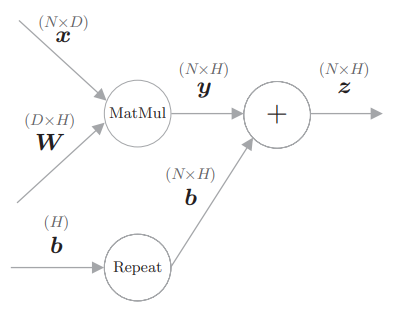
image-20220316144659123 
class Affine:
    def __init__(self, W, b):
        self.params = [W, b]
        self.grads = [np.zeros_like(W), np.zeros_like(b)]
        self.x = None

    def forward(self, x):
        W, b = self.params
        out = np.dot(x, W) + b
        self.x = x
        return out

    def backward(self, dout):
        W, b = self.params
        dx = np.dot(dout, W.T)
        dW = np.dot(self.x.T, dout)
        db = np.sum(dout, axis=0)

        self.grads[0][...] = dW
        self.grads[1][...] = db
        return dx
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 3.5.3 Softmax with Loss 层

我们将 Softmax 函数和交叉熵误差一起实现为 Softmax with Loss 层：

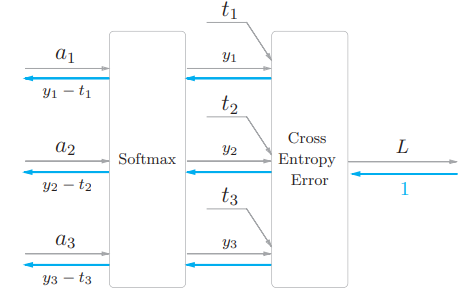
image-20220316144829242
  • 这里假设要执行 3 类别分类的任务，从前一层（靠 近输入的层）接收 3 个输入。Softmax 层对输入 进行正规化，输出 。Cross Entropy Error 层接收 Softmax 的输出 和监督标签 ，并基于这些数据输出损失 L。
class SoftmaxWithLoss:
    def __init__(self):
        self.params, self.grads = [], []
        self.y = None  # softmax的输出
        self.t = None  # 监督标签

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)

        # 在监督标签为one-hot向量的情况下，转换为正确解标签的索引
        if self.t.size == self.y.size:
            self.t = self.t.argmax(axis=1)

        loss = cross_entropy_error(self.y, self.t)
        return loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]

        dx = self.y.copy()
        dx[np.arange(batch_size), self.t] -= 1
        dx *= dout
        dx = dx / batch_size

        return dx
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 3.6 权重的更新

通过误差反向传播法求出梯度后，就可以使用该梯度更新神经网络的参 数。此时，神经网络的学习按如下步骤进行：

  • 步骤 1：【mini-batch】从训练数据中随机选出多笔数据
  • 步骤 2：【计算梯度】基于误差反向传播法，计算损失函数关于各个权重参数的梯度
  • 步骤 3：【更新参数】使用梯度更新权重参数。
  • 步骤 4：【重复】重复下面步骤

首先，选择 mini-batch 数据，根据误差反向传播法获得权重的梯度。这个梯度指向当前的权重参数所处位置中损失增加最多的方向。因此，通过将参数向该梯度的反方向更新，可以降低损失。这就是梯度下降法（gradient descent）。之后，根据需要将这一操作重复多次即可。

我们在上面的步骤 3 中更新权重。权重更新方法有很多，这里我们来 实现其中最简单的随机梯度下降法（Stochastic Gradient Descent，SGD）。 其中，“随机”是指使用随机选择的数据（mini-batch）的梯度。

SGD 是一个很简单的方法。它将（当前的）权重朝梯度的（反）方向更新一定距离：

  • 这里将要更新的权重参数记为 W，损失函数关于 W 的梯度记为 。 表示学习率。

进行参数更新的类的实现拥有通用方法update(params, grads)：

class SGD:
    '''
    随机梯度下降法（Stochastic Gradient Descent）
    '''
    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for i in range(len(params)):
            params[i] -= self.lr * grads[i]
1
2
3
4
5
6
7
8
9
10

使用这个 SGD 类，神经网络的参数更新可按如下方式进行：

model = TwoLayerNet(...)
optimizer = SGD()

for i in range(10000):
	...
	x_batch, t_batch = get_mini_batch(...) # 获取mini-batch
	loss = model.forward(x_batch, t_batch)
	model.backward()
	optimizer.update(model.params, model.grads)
	...
1
2
3
4
5
6
7
8
9
10

# 3.7 Trainer 类

我们 将进行学习的类作为 Trainer 类提供出来，使用起来就像：

model = TwoLayerNet(...)
optimizer = SGD(lr=1.0)
trainer = Trainer(model, optimizer)
1
2
3

然后调用 fit() 方法开始学习，其参数如下：

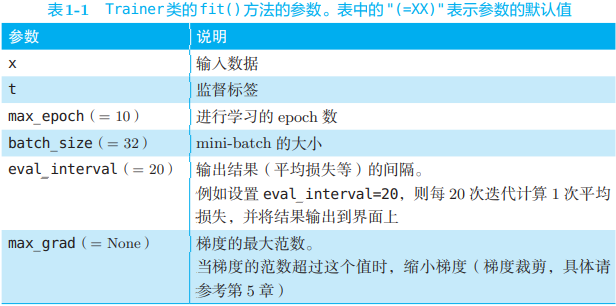
image-20220316150449737

具体代码可见附带的资源。

# 3.9 示例

import sys
sys.path.append('..')
from common.optimizer import SGD
from common.trainer import Trainer
from dataset import spiral
from two_layer_net import TwoLayerNet

max_epoch = 300
batch_size = 30
hidden_size = 10
learning_rate = 1.0

x, t = spiral.load_data()
model = TwoLayerNet(input_size=2, hidden_size=hidden_size, output_size=3)
optimizer = SGD(lr=learning_rate)

trainer = Trainer(model, optimizer)
trainer.fit(x, t, max_epoch, batch_size, eval_interval=10)
trainer.plot()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 4. 计算的高速化

# 4.1 位精度

NumPy 的浮点数默认使用 64 位的数据类型。但是，我们已经知道使用 32 位浮点 数也可以无损地（识别精度几乎不下降）进行神经网络的推理和学习。在神经网络的计算中，数据传输的总线带宽有时会成为瓶颈。在这种情况下，毫无疑问数据类型也是越小越好。再者，就计算速度而言，32 位浮点数也能更高速地进行计算（浮点数的计算速度依赖于 CPU 或 GPU 的 架构）。因此，本书优先使用 32 位浮点数。

要在 NumPy 中使用 32 位浮点数，可以像下面这样将数据类型指定为 np.float32 或者 'f'：

>>> b = np.random.randn(3).astype(np.float32)
>>> b.dtype
dtype('float32')

>>> c = np.random.randn(3).astype('f')
>>> c.dtype
dtype('float32')
1
2
3
4
5
6
7

虽然 NumPy 中准备有16 位浮点数，但是普通 CPU 或 GPU 中的运算是用 32 位执行的。因此， 即便变换为 16 位浮点数，因为计算本身还是用 32 位浮点数执行的，所以处 理速度方面并不能获得什么好处。但是，如果是要（在外部文件中）保存学习好的权重，则 16 位浮点数是有用的。具体地说，将权重数据用 16 位精度保存时，只需要 32 位时的一半容量。因此，本书仅在保存学习好的权重时，将其变换为 16 位浮点数。

# 4.2 GPU（CuPy）

深度学习的计算是 GPU 比 CPU 擅长的地方。CuPy 是基于 GPU 进行并行计算的库。使用 CuPy，可以轻松地使用 NVIDIA 的 GPU 进行并行计算。更重要的是，CuPy 和 NumPy 拥有共同的 API。

>>> import cupy as cp
>>> x = cp.arange(6).reshape(2, 3).astype('f')
>>> x
array([[ 0., 1., 2.],
 [ 3., 4., 5.]], dtype=float32)

>>> x.sum(axis=1)
array([ 3., 12.], dtype=float32)
1
2
3
4
5
6
7
8
编辑 (opens new window)
上次更新: 2022/08/26, 13:48:42
torch.nn 之 Module、ModuleList 和 Sequential
自然语言和单词的分布式表示

← 自然语言和单词的分布式表示→

最近更新
01
Deep Reinforcement Learning
10-03
02
误删数据后怎么办
04-06
03
MySQL 一主多从
03-22
更多文章>
Theme by Vdoing | Copyright © 2021-2024 yubincloud | MIT License
×