notebook
yubin
2022-03-16
目录

自然语言和单词的分布式表示

自然语言处理涉及多个子领域，但是它们的根本任务都是让计算机理解我们的语言。本章先详细考察古典方法，即深度学习出现以前的方法。本章我们还会练习使用 Python 处理文本，实现分词（将文本分割成单 词）和单词 ID 化（将单词转换为单词 ID）等任务。

我们的语言是由文字构成的，而语言的含义是由单词构成的。换句话说，单词是含义的最小单位。本章的主题探讨一些巧妙地蕴含了单词含义的表示方法：

  • 基于同义词词典的方法【本章】
  • 基于计数的方法【本章】
  • 基于推理的方法【下一章】

# 1. 基于同义词词典的方法

要表示单词含义，首先可以考虑通过人工方式来定义单词含义。一种方法是像《新华字典》那样，一个词一个词地说明单词含义。通过像这样定义单词，计算机或许也能够理解单词含义。

这种思路下，被广泛使用的是一种被称为同义词词典（thesaurus）的词典。在同义词词典中，具有相同含义的单词（同义词）或含义类似的单词（近义词）被归类到同一个组中。比如，使用同义词词典，我们可以知道 car 的同义词有 automobile、motorcar 等。

另外，同义词词典有时会定义单词之间的粒度 更细的关系，比如“上位 - 下位”关系、“整体 - 部分”关系，比如：

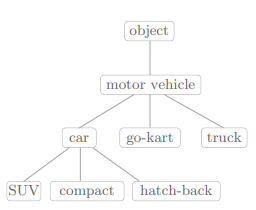
image-20220318192650717

像这样，通过对所有单词创建近义词集合，并用图表示各个单词的关系，可以定义单词之间的联系。利用这个“单词网络”，可以教会计算机单词之间的相关性。也就是说，我们可以将单词含义（间接地）教给计算机，然后利用这一知识，就能让计算机做一些对我们有用的事情。

如何使用同义词词典根据自然语言处理的具体应用的不同而不同。比如，在信息检索场景中，如果事先知道 automobile 和 car 是近义词，就可以将 automobile 的检索结果添加到 car 的检索结果中。

# 1.1 WordNet

在自然语言处理领域，最著名的同义词词典是 WordNet。使用 WordNet，可以获得单词的近义词，或者利用单词网络。使用单词网络，可以计算单词之间的相似度。

WordNet 是普林斯顿大学于 1985 年开始开发的同义词词典，迄今已用于许多研究，并活跃于各种自然语言处理应用中。

# 1.2 同义词词典的问题

WordNet 等同义词词典中对大量单词定义了同义词和层级结构关系等。利用这些知识，可以（间接地）让计算机理解单词含义。不过这种人工标记也存在较大的缺陷：

  • 难以顺应时代变化：随着时间的推移，新词会不断出现
  • 人力成本高：制作词典需要巨大的人力成本
  • 无法表示单词的微妙差异：实际上， 即使是含义相近的单词，也有细微的差别，而这种细微的差别在同义词词典中 是无法表示出来的

由于以上的问题，将要介绍的绍基于计数的方法和利用神经网络的基于推理的方法可以从海量的文本数据中自动提取单词含义，将我们从人工关联单词的辛苦劳动中解放出来。

# 2. 基于计数的方法

从介绍基于计数的方法开始，我们将使用语料库（corpus），它一般收集的都是用于自然语言处理研究和应用的文本数据。基于计数的方法的目标就是从这些富有实践知识的语料库中，自动且高效地提取本质。

自然语言处理领域中使用的语料库有时会给文本数据添加额外的信息。比如，可以给文本数据的各个单词标记词性。在这种情况下，为了方便计算机处理，语料库通常会被结构化（比如，采用树结构等数据形式）。这里，假定我们使用的语料库没有添加标签，而是作为一个大的文本文件，只包含简单的文本数据。

# 2.1 基于 Python 的语料库的预处理

说到有名的语料库，有 Wikipedia 和 Google News 等。另外，莎士比亚、夏目漱石等伟大作家的作品集也会被用作语料库。本章我们先使用仅包含一个句子的简单文本作为语料库，然后再处理更实用的语料库。

我们首先对对一个非常小的文本数据（语料库）进行预处理。这里所说的预处理是指，将文本分割为单词（分词），并将分割后的单词列表转化为单词 ID 列表。

我们语料库是：

>>> text = 'You say goodbye and I say hello.'
1

首先对 text 进行分词：

>>> text = text.lower()  # 将所有字母转化为小写
>>> text = text.replace('.', ' .')
>>> text
'you say goodbye and i say hello .'

>>> words = text.split(' ')  # 将空格作为分隔符
>>> words
['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']
1
2
3
4
5
6
7
8
  • 考虑到句子结尾处的句号（.），我们先在句号前插入一个空格（即用“ .”替换“.”），再进行分词。

分词时，我们采用了一种在句号前插入空格的 “临时对策”，其实还有更加 聪明、更加通用的实现方式，比如正则表达式，使用 re.split('(\W+)?', text) 进行分词。

现在我们已经可以将原始文章作为单词列表使用了。虽然分词后文本更容易处理了，但是直接以文本的形式操作单词，总感觉有些不方便。因此，我们进一步给单词标上 ID，以便使用单词 ID 列表。为此，我们使用 Python 的字典来创建单词 ID 和单词的对应表：

>>> word_to_id = {}  # 将单词 ID 转化为单词
>>> id_to_word = {}  # 将单词转化为单词 ID
>>>
>>> for word in words:
... 	if word not in word_to_id:
... 		new_id = len(word_to_id)  # 将字典的长度设为新的单词 ID，从而实现递增
... 		word_to_id[word] = new_id
... 		id_to_word[new_id] = word
1
2
3
4
5
6
7
8
  • 这里，我们从头开始逐一观察分词后 的 words 的各个元素，如果单词不在 word_to_id 中，则分别向 word_to_id 和 id_to_word 添加新 ID 和单词。

这样一来，我们就创建好了单词 ID 和单词的对应表。下面，我们来实际看一下它们的内容：

>>> id_to_word
{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6:'.'}
>>> word_to_id
{'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}
1
2
3
4

使用这些词典，可以根据单词检索单词 ID，或者反过来根据单词 ID 检索单词。

最后，我们将单词列表转化为单词 ID 列表：

>>> import numpy as np
>>> corpus = [word_to_id[w] for w in words]
>>> corpus = np.array(corpus)
>>> corpus
array([0, 1, 2, 3, 4, 1, 5, 6])
1
2
3
4
5

至此，我们就完成了利用语料库的准备工作。现在，我们将上述一系列处理实现为 preprocess() 函数：

def preprocess(text):
    text = text.lower()
    text = text.replace('.', ' .')
    words = text.split(' ')

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

使用这个函数，可以按如下方式对语料库进行预处理：

>>> text = 'You say goodbye and I say hello.'
>>> corpus, word_to_id, id_to_word = preprocess(text)
1
2

这里准备的 corpus、word_to_id 和 id_to_word 这 3 个变量名在本书接下来的很多地方都会用到：corpus 是单词 ID 列表，word_to_id 是单词到单词 ID 的字典，id_to_word 是单词 ID 到单词 的字典。

现在，我们已经做好了操作语料库的准备，接下来的目标就是使用语料库提取单词含义。我们将考察基于计数的方法。采用这种方法，我们能够将单词表示为向量

# 2.2 单词的分布式表示

使用 RGB 这样的向量表示可以更准确地指定颜色，并且这种基于三原色的表示方式很紧凑。而在自然语言处理领域，能准确把握单词含义的密集向量表示（各元素大多数非 0），这称为分布式表示。

# 2.3 分布式假设

在自然语言处理的历史中，用向量表示单词的研究有很多。但几乎所有的重要方法都基于一个简单的想法，这个想法就是“某个单词的含义由它周围的单词形成”，称为分布式假设（distributional hypothesis）。其表达的理念就是，单词本身没有含义，单词含义由它所在的上下文（语境）形成。

我们经常使用“上下文”一词，指指某个单词（关注词）周围的单词：

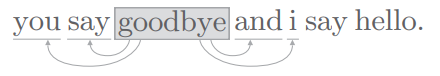
image-20220318203553350
  • 我们将上下文的大小（即周围的单词有多少个）称为窗口大小。比如窗口大小为 1，上下文包含左右各 1 个单词。

这里，我们将左右两边相同数量的单词作为上下文。但是，根据具体情况，也可以仅将左边的单词或者右边的单词作为上下文。简单起见，我们仅处理理不考虑句子分隔符、左右单词数量相同的上下文。

# 2.4 共现矩阵

我们来考虑如何基于分布式假设使用向量表示单词，最直截了当的实现方法是对周围单词的数量进行计数。具体来说，在关注某个单词的情况下，对它的周围出现了多少次什么单词进行计数，然后再汇总。这种做法称为“基于计数的方法”，在有的文献中也称为“基于统计的方法”。

我们先使用之前的语料库和 preprocess() 函数，再次进行预处理：

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
1
2

下面，我们计算每个单词的上下文所包含的单词的频数。在这个例子中，我们将窗口大小设为 1，从单词 ID 为 0 的 you 开始。

image-20220318205549565

用表格表示单词 you 的上下文中包含的单词的频数：

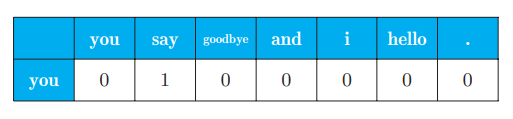
image-20220318205625946

这意味着可以用向量 [0, 1, 0, 0, 0, 0, 0] 表示单词 you。

接着对单词 ID 为 1 的 say 进行同样的处理，可以得到如下结果：

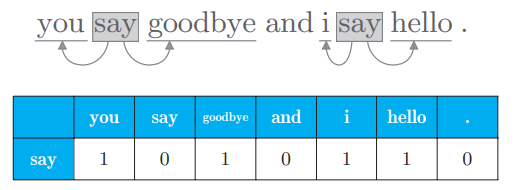
image-20220318205800504

由此单词 say 可以表示为向量 [1, 0, 1, 0, 1, 1, 0]。对所有的 7 个单词进行上述操作，会得到如下的结果：

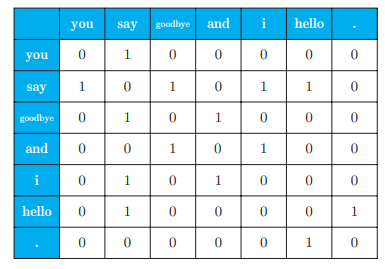
image-20220318205905230

上图是汇总了所有单词的共现单词的表格。这个表格的各行对应相应单词的向量，这个表格被称为共现矩阵（co-occurence matrix）。

我们来获得这个共现矩阵，把这个函数称为 create_co_matrix(corpus, vocab_size, window_size=1)，其中参数 corpus 是单词 ID 列表，参数 vocab_ size 是词汇个数，window_size 是窗口大小。

def create_co_matrix(corpus, vocab_size, window_size=1):
    '''生成共现矩阵

    :param corpus: 语料库（单词ID列表）
    :param vocab_size:词汇个数
    :param window_size:窗口大小（当窗口大小为1时，左右各1个单词为上下文）
    :return: 共现矩阵
    '''
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1

            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1

    return co_matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
  • 首先，用元素为 0 的二维数组对 co_matrix 进行初始化。然后，针对语料库中的每一个单词，计算它的窗口中包含的单词。同时，检查窗口内的单词是否超出了语料库的左端和右端。

这个函数便可以创建出一个共现矩阵。

# 2.5 向量间的相似度

前面我们通过共现矩阵将单词表示为了向量。下面，我们看一下如何测量向量间的相似度。

测量量向量间的相似度的方法中，具有代表性的方法有向量内积或欧式距离等。余弦相似度（cosine similarity）是很常用的一种，公式为：

  • 分子是向量内积，分母是各向量的 L2 范数。
  • 要点是先对向量进行正规化，再求它们的内积

余弦相似度直观地表示了“两个向量在多大程度上指向同一方向”。两个向量完全指向相同的方向时，余弦相似度为 1；完全指向相反的方向时，余弦相似度为 −1。

现在我们实现余弦相似度：

def cos_similarity(x, y):
	nx = x / np.sqrt(np.sum(x**2)) # x 的正规化
	ny = y / np.sqrt(np.sum(y**2)) # y 的正规化
	return np.dot(nx, ny)
1
2
3
4

这里余弦相似度的实现虽然完成了，但是还有一个问题。那就是当零向量（元素全部为 0 的向量）被赋值给参数时，会出现 “除数为 0”（zero division）的错误。

解决此类问题的一个常用方法是，在执行除法时加上一个微小值。这里，通过参数指定一个微小值 eps（eps 是 epsilon 的缩写），并默认 eps=1e-8（= 0.000 000 01）。这样修改后的余弦相似度的实现如下所示：

def cos_similarity(x, y, eps=1e-8):
    '''计算余弦相似度

    :param x: 向量
    :param y: 向量
    :param eps: 用于防止“除数为0”的微小值
    :return:
    '''
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
    return np.dot(nx, ny)
1
2
3
4
5
6
7
8
9
10
11

利用这个函数，可以如下求得单词向量间的相似度。这里，我们尝试求 you 和 i（= I）的相似度：

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)

c0 = C[word_to_id['you']]  #you的单词向量
c1 = C[word_to_id['i']]  #iの单词向量
print(cos_similarity(c0, c1))
# 0.7071067691154799
1
2
3
4
5
6
7
8
9

从上面的结果可知，you 和 i 的余弦相似度是 0.70 ...，所以这两个词之间存在相似性。

# 2.6 相似单词的排序

余弦相似度已经实现好了，使用这个函数，我们可以实现另一个便利的 函数：当某个单词被作为查询词时，将与这个查询词相似的单词按降序显示出 来。这里将这个函数称为 most_similar()：

def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    '''相似单词的查找

    :param query: 查询词
    :param word_to_id: 从单词到单词ID的字典
    :param id_to_word: 从单词ID到单词的字典
    :param word_matrix: 汇总了单词向量的矩阵，假定保存了与各行对应的单词向量
    :param top: 显示到前几位
    '''
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('\n[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

上述实现按如下顺序执行：

  1. 取出查询词的单词向量。
  2. 分别求得查询词的单词向量和其他所有单词向量的余弦相似度。
  3. 基于余弦相似度的结果，按降序显示它们的值。

有了 most_ similar() 函数，我们将 you 作为查询词， 显示与其相似的单词：

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)

most_similar('you', word_to_id, id_to_word, C, top=5)
1
2
3
4
5
6

执行代码后，会得到如下结果：

[query] you
 goodbye: 0.7071067691154799
 i: 0.7071067691154799
 hello: 0.7071067691154799
 say: 0.0
 and: 0.0
1
2
3
4
5
6

观察上面的结果可知，和 you 最接近的单词有 3 个，分别是 goodbye、i（= I）和 hello。也许和我们的感觉存在很大的差异。一个可能的原因是，这里的语料库太小了。

如上所述，我们通过共现矩阵成功地将单词表示为了向量。至此，基于计数的方法的基本内容就介绍完了。下一节，我们将说明当前方法的改进思路，并实现这个改进思路。

# 3. 基于计数的方法的改进

// TODO 可见鱼书的 2.4 节

编辑 (opens new window)
上次更新: 2022/08/26, 13:48:42
神经网络的复习
word2vec

← word2vec→

最近更新
01
Deep Reinforcement Learning
10-03
02
误删数据后怎么办
04-06
03
MySQL 一主多从
03-22
更多文章>
Theme by Vdoing | Copyright © 2021-2024 yubincloud | MIT License
×