上一章实现的简单的 CBOW 模型存在几个问题，其中最大的问题是，随着语料库中处理的词汇量的增加，计算量也随之显著增加。本章将重点放在 word2vec 的加速上，来改善 word2vec：

• 引入名为 Embedding 层的新层
• 引入名为 Negative Sampling 的新损失函数

复习一下上一章的 CBOW 模型：

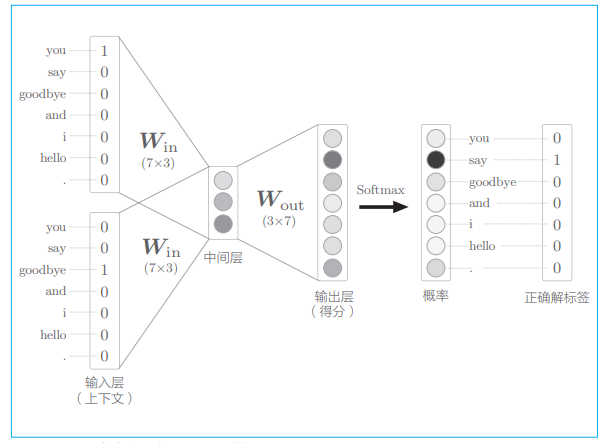
在处理大规模语料库时，这个模型就存在多个问题了。假设词汇量有 100 万个，输入层和输出层存在 100 万个神经元。此时以下两个地方的计 算会出现瓶颈：

• 输入层的 one-hot 表示和权重矩阵 的乘积。这个问题通过引入 Embedding 层来解决。
• 中间层和权重矩阵 的乘积以及 Softmax 层的计算。这个问题通过引入 Negative Sampling 这一新的损失函数来解决。

1. word2vec 改进 —— Embedding

1.1 Embedding 层

我们来考虑词汇量是 100 万个的情况，one-hot 表示的上下文和 MatMul 层的权重的乘积如下图所示：

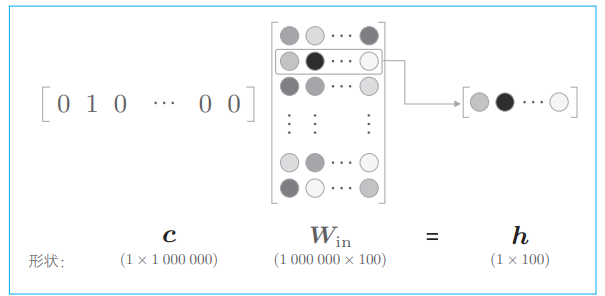
此时我们需要计算这个巨大向量和权重矩阵的乘积，但如图所示，所做的无非是将矩阵的某个特定的行取出来，因此做这个矩阵乘法是没有必要的。

我们创建一个从权重参数中抽取“单词 ID 对应行（向量）”的 层，这里我们称之为 Embedding 层。

Embedding，“词嵌入”，该层存放词嵌入（分布式表示）。在 NLP 中，单词的密集向量表示称为词嵌入（word embedding）或者单词的分布式表示（distributed representation）。

1.2 Embedding 层的实现

假设权重 W 是二维数组，如果要从这个权重中取出某个特定的行，只需写 W[2] 或者 W[5] 即可。另外，从权重 W 中一次性提取多行的处理也很简单。只需通过数组指定行号即可，比如 W[[2, 5]] 便提取出 2、5 行，这种提取用于 mini-batch 处理。

下面，我们来实现 Embedding 层的 forward() 方法：

class Embedding:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.idx = None

    def forward(self, idx):
        W, = self.params
        self.idx = idx
        out = W[idx]
        return out

• 在成员变量 idx 中以数组的形式保存需要提取的行的索引（单词 ID）

接下来，我们考虑反向传播。Embedding 层的正向传播只是从权重矩阵 W 中提取特定的行，并将该特定行的神经元原样传给下一层。因此，在反向传播时，从上一层（输出侧的层）传过来的梯度将原样传给下一层（输入侧的层）：

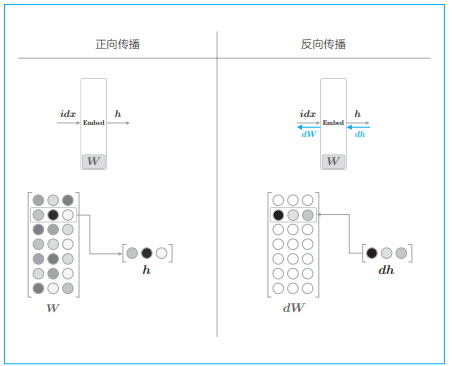
实现 backward() 如下：

def backward(self, dout):
    dW, = self.grads
    dW[...] = 0
    if GPU:
        np.scatter_add(dW, self.idx, dout)
    else:
        np.add.at(dW, self.idx, dout)
    return None

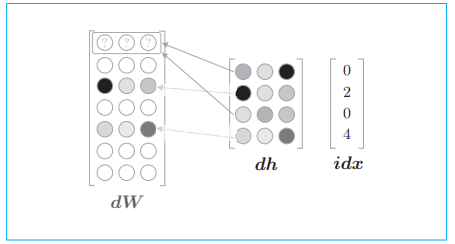
• 这里，取出权重梯度 dW，通过 dW[...] = 0 将 dW 的元素设为 0（并不是将 dW 设为 0，而是保持 dW 的形状不变，将它的元素设为 0）。然后，将上一层传来的梯度 dout 写入 idx 指定的行。
• 使用 add 来修改 dW 是因为当 idx 中的元素出现重复时，比如 idx=[0,2,0,4] 时会发生下图的情况，这时应该把 dh 各行的值累加到 dW 的对应行中：

这里创建了和权重 W 相同大小的矩阵 dW，并将梯度写入了 dW 对应的行。但是，我们最终想做的事情是更新权重 W，所以没有必要特意创建 dW（大小与 W相同）。相反，只需把需要更新的行号（idx）及其对应的梯度（dout）保存下来，就可以更新权重（W）的特定行。但是，这里为了兼容已经实现的优化器类，所以写成了现在的样子。

关于 Embedding 层的实现就介绍到这里。现在，我们可以将 word2vec（CBOW 模型）的实现中的输入侧的 MatMul 层换成 Embedding 层。这样 一来，既能减少内存使用量，又能避免不必要的计算。

2. word2vec 改进 —— 负采样

在上一节中，通过引入 Embedding 层，节省了输入层中不必要的计算。剩下的问题就是中间层之后的处理。此时，在以下两个地方需要很多计算时间：

• 中间层的神经元和权重矩阵（）的乘积
• Softmax 层的计算

第 1 个问题在于巨大的矩阵乘积计算，所以很有必要将矩阵乘积计算轻量化。

其次，Softmax 也会发生同样的问题。观察 softmax 的公式： 可知这个计算也与词汇量成正比，因此需要一个可以替代 Softmax 的轻量的计算。

2.1 从多分类到二分类

我们来解释一下负采样。这个方法的关键思想是用二分类拟合多分类。

二分类处理的是答案为“Yes/No”的问题，比如“目标词是 say 吗”

之前我们处理的都是多分类问题，把它看作了从 100 万个单词中选择 1 个正确单词的任务，比如对于“当上下文是 you 和 goodbye 时，目标词是什么？”这个问题，神经网络可以给出正确答案。现在我们来考虑如何将多分类问题转化为二分类问题。比如，让神经网络来回答“当上下文是 you 和 goodbye 时，目标词是 say 吗？”这个问题，这时输出层只需要一个神经元即可，可以认为输出层的神经元输出的是 say 的得分。

此时 CBOW 的模型可以表示为下图：

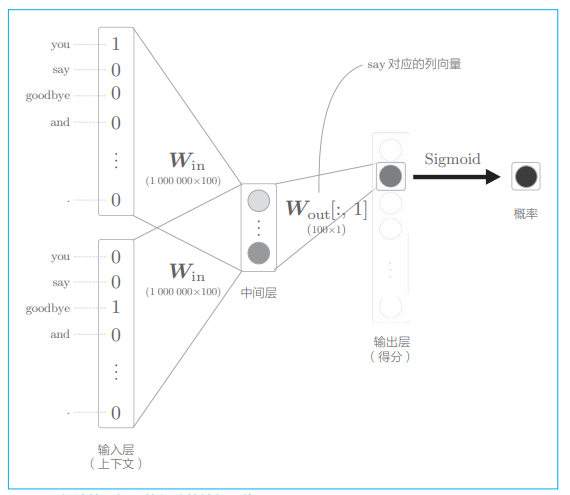
如上图，输出层的神经元仅有一个。因此，要计算中间层和输出侧的权重矩阵的乘积，只需要提取 say 对应的列（单词向量），并用它与中间层的神经元计算内积即可，这个过程如下图：

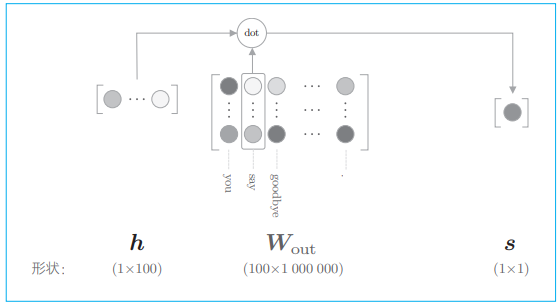
如上图，输出侧的权重 中保存了各个单词 ID 对应的单词向量。此处，我们提取 say 这个单词向量，再求这个向量和中间层神经元的内积，这就是最终的得分。这个得分会经过 sigmoid 函数将其转换为概率。

2.2 sigmoid 函数和交叉熵误差

要使用神经网络解决二分类问题，需要使用 sigmoid 函数将得分转化为概率。为了求损失，我们用交叉熵误差作为损失函数。这些都是二分类神经网络的老套路。

多分类时，输出层使用 softmax 将得分转换成概率，损失函数使用交叉熵误差；在二分类中，输出层使用 sigmoid，损失函数也使用交叉熵误差。

sigmoid 函数：，输入 x 被转化为 0-1 之间的实数，这个输出 y 可以被解释为概率。Softmax 层如下：

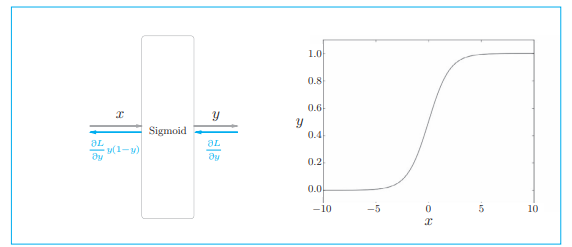
通过 sigmoid 函数得到概率 y 后，可以由概率 y 用交叉熵误差来计算损失，其数学表达式为：

• y 是 sigmoid 的输出
• t 是正确解标签，取值 0/1：0 表示正确解是 “Yes”，0 表示正确解是 “No”

二分类和多分类的损失函数均为交叉熵误差，两者的数学式只是写法不同而已。

我们用图来表示 Sigmoid 层和 Cross Entropy Error 层：

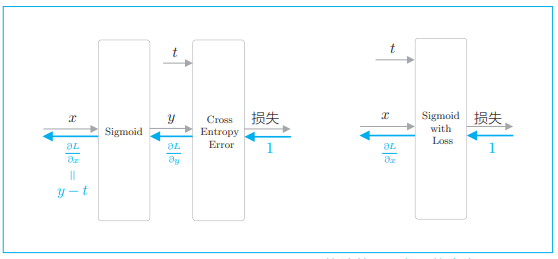
• 值得注意的是反向传播的 y − t 这个值。y 是神经网络输出的概率，t 是正确解标签，y − t 正好是这两个值的差。这意味着，当正确解标签是 1 时，如果 y 尽可能地接近 1（100%），误差将很小。反过来，如果 y 远离 1，误差将增大。随后，这个误差向前面的层传播，当误差大时，模型学习得多；当误差小时，模型学习得少。

2.3 多分类到二分类的实现

之前我们处理了多分类问题，在输出层使用了与词汇量同等数量的神经元，此时神经网络可以画为如下的图：

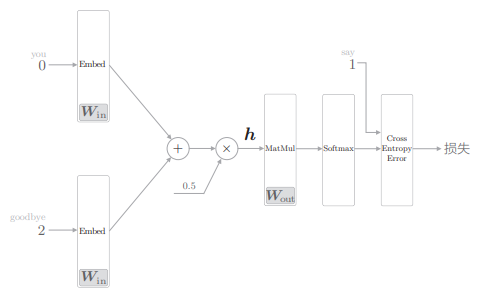
• 上下文是 you 和 goodbye、作为正确解的目标词是 say。数字分别表示其单词 ID

现在我们将其转化成二分类的神经网络：

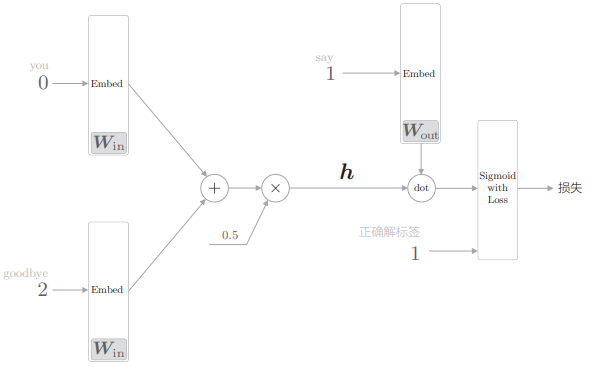
• 这里，将中间层的神经元记为 h，并计算它与输出侧权重 中的单词 say 对应的单词向量的内积。然后，将其输出输入 Sigmoid with Loss 层，得到最终的损失
• 正确解标签输入 1 表示现在正在处理的问题的答案是“Yes”，输入 0 表示“No”。比如这个例子表示：上下文为 you、goodbye 时，答案 say 是正确的。

为了便于理解，我们将后半部分的 Embedding 层和 dot 内积运算合并成 Embedding Dot 层，于是这个网络的后半部分可以画成：

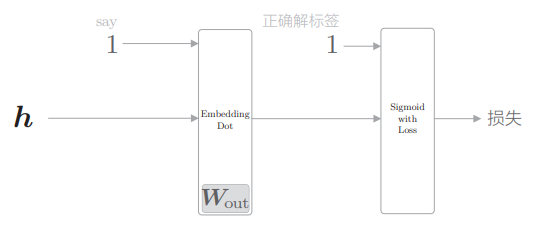
• 中间层的神经元 h 流经 Embedding Dot 层，传给 Sigmoid with Loss 层。

Embedding Dot 层的实现：

class EmbeddingDot:
    def __init__(self, W):
        self.embed = Embedding(W)
        self.params = self.embed.params
        self.grads = self.embed.grads
        self.cache = None

    def forward(self, h, idx):
        target_W = self.embed.forward(idx)
        out = np.sum(target_W * h, axis=1)

        self.cache = (h, target_W)
        return out

    def backward(self, dout):
        h, target_W = self.cache
        dout = dout.reshape(dout.shape[0], 1)

        dtarget_W = dout * h
        self.embed.backward(dtarget_W)
        dh = dout * target_W
        return dh

• cache 保存正向传播时的计算结果
• 正向传播接收中间层的神经元（h）和单词 ID 的列表（idx），因为这里我们假定对数据进行了 mini-batch 处理
• np.sum(self.target_W * h, axis=1) 计算内积

上面各变量的一个实例：

• 因为 idx 是 [0, 3, 1]，所以 target_W 将提取出 W 的第 0 行、第 3 行和第 1 行。
• target_W * h 计算对应元素的乘积，然后对结果逐行（axis=1）求和，得到 out

2.4 负采样

至此我们已经成功地把要解决的问题从多分类问题转化成了二分类问题，但目前我们仅学习了正例（正确答案），还不确定负例（错误答案）会有怎样的结果。

比如之前例子的模型，在上下文是 you、goodbye 时，对正例 say 进行二分类，其 sigmoid 的输出概率应当接近 1，但它现在对 say 之外的负例一无所知，我们还应该让它对于负例使 sigmoid 输出接近 0：

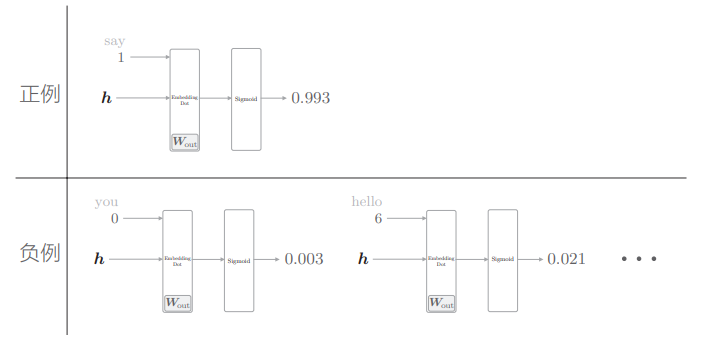
笔记

为了把多分类问题处理为二分类问题，对于“正确答案”（正例）和“错误答案”（负例），都需要能够正确地进行分类（二分类）。因此，需要同时考虑正例和负例。

但不应该以所有负例为对象进行学习，否则会使计算暴增。作为一种近似方法，我们将选择少数负例，这就是负采样方法的含义。

总之，负采样方法求正例作为目标词的损失和采样若干负例求损失，并将正负例的损失加起来，作为最终的损失。

再次使用之前的例子，并加入两个负例目标词 hello 和 i，只关注 CBOW 模型的中间部分，则负采样的计算图如下：

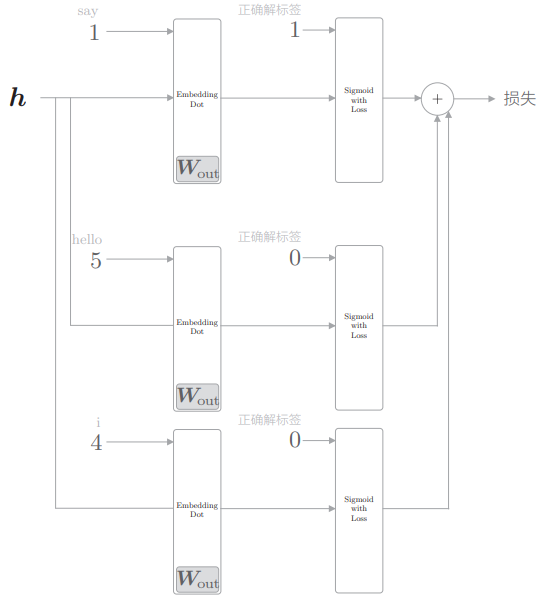
• 负例是错误答案，所以应该向 Sigmoid with Loss 层输入正确解标签 0。

2.5 负采样的采样方法

下面看一下如何抽取负例。基于语料库的统计数据进行采样的方法比随机抽样要好。具体来说，就是让语料库中经常出现的单词容易被抽到，让语料库中不经常出现的单词难以被抽到。

基于语料库中单词使用频率的采样方法会先计算语料库中各个单词的出现次数，并将其表示为“概率分布”，然后使用这个概率分布对单词进行采样：

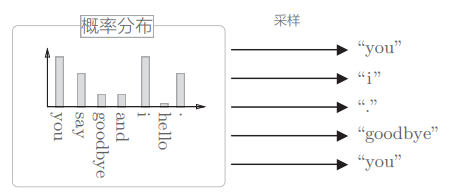
为在现实问题中， 稀有单词基本上不会出现，所以处理稀有单词的重要性较低。 相反，处理好高频单词才能获得更好的结果。

在 Python 中，np.random.choice() 可以用于随机抽样：

• 若指定 size 参数，将多次采样
• 若指定 replace=False，将进行无放回采样
• 若指定参数 p 为概率分布的列表，将进行基于概率分布的采样

如下例：

>>> words = ['you', 'say', 'goodbye', 'I', 'hello', '.']
>>> p = [0.5, 0.1, 0.05, 0.2, 0.05, 0.1]
>>> np.random.choice(words, p=p)
'you'

word2vec 中提出的负采样对刚才的概率分布增加了一个步骤，如下面的式子所示，它对原来的概率分布取 0.75 次方：

• 表示第 个单词的概率

进行上面这个变换是为了防止低频单词被忽略。通过取 0.75 次方，低频单词的概率将稍微变高。此外，0.75 这个值并没有什么理论依据，也可以设置成其他的值。

我们将负采样的处理实现为 UnigramSampler 类，下面做简单说明。

PS：unigram 是“1 个(连续)单词”的意思。同样地，bigram 是“2 个 连续单词”的意思，trigram 是“3 个连续单词”的意思。这里使用 UnigramSampler 这个名字，是因为我们以 1 个单词为对象创建概率分布。如果是 bigram，则 以 ( you’, ‘say’)、‘( you’, ‘goodbye’)……这样的 2 个单词的组合为对象创建概率分布。

UnigramSampler 类介绍：

• UnigramSampler 类初始化接收 3 个参数：单词 ID 列表格式的 corpus、对概率分布取的次方值 power 和负例的采样个数 sample_size。
• get_negative_sample(target) 方法以参数 target 指定的单词 ID 为正例，对其他的单词 ID 进行采样。

使用示例：

corpus = np.array([0, 1, 2, 3, 4, 1, 2, 3])
power = 0.75
sample_size = 2

sampler = UnigramSampler(corpus, power, sample_size)
target = np.array([1, 3, 0])
negative_sample = sampler.get_negative_sample(target)
print(negative_sample)
# [[0 3]
# [1 2]
# [2 3]]

• 这里将 [1, 3, 0] 这 3 个数据的 mini-batch 作为正例，对各个数据采样 2 个负例。

2.6 负采样的实现

我们来实现负采样。将其实现为 NegativeSamplingLoss 类。

2.6.1 初始化

参照上面负采样的计算图，可以写出如下代码：

class NegativeSamplingLoss:
    def __init__(self, W, corpus, power=0.75, sample_size=5):
        self.sample_size = sample_size
        self.sampler = UnigramSampler(corpus, power, sample_size)
        self.loss_layers = [SigmoidWithLoss() for _ in range(sample_size + 1)]
        self.embed_dot_layers = [EmbeddingDot(W) for _ in range(sample_size + 1)]

        self.params, self.grads = [], []
        for layer in self.embed_dot_layers:
            self.params += layer.params
            self.grads += layer.grads

• 生成 UnigramSampler 类，并使用成员变量 sampler 保存
• 负例的采样数设置为成员变量 sample_size
• 成员变量 loss_layers 和 embed_dot_layers 中以列表格式保存了必要的层。在这两个列表中生成 sample_size + 1 个层，这是因为需要生成一个正例用的层和 sample_size 个负例用的层。这里假定列表的第一个层处理正例。

2.6.2 forward

forward(h, target) 方法接收的参数是中间层的神经元 h 和正例目标词 target。它首先使用 self.sampler 采样负例，并设为 negative_sample。然后，分别对正例和负例的数据进行正向传播，求损失的和。具体而言，通过 Embedding Dot 层的 forward 输出得分，再将这个得分和标签一起输入 Sigmoid with Loss 层来计算损失。

def forward(self, h, target):
    batch_size = target.shape[0]
    negative_sample = self.sampler.get_negative_sample(target)

    # 正例的正向传播
    score = self.embed_dot_layers[0].forward(h, target)
    correct_label = np.ones(batch_size, dtype=np.int32)
    loss = self.loss_layers[0].forward(score, correct_label)

    # 负例的正向传播
    negative_label = np.zeros(batch_size, dtype=np.int32)
    for i in range(self.sample_size):  # i 表示第 i 个负例
        negative_target = negative_sample[:, i]
        score = self.embed_dot_layers[1 + i].forward(h, negative_target)
        loss += self.loss_layers[1 + i].forward(score, negative_label)

    return loss

2.6.3 backward

def backward(self, dout=1):
    dh = 0
    for l0, l1 in zip(self.loss_layers, self.embed_dot_layers):
        dscore = l0.backward(dout)
        dh += l1.backward(dscore)

    return dh

反向传播的实现非常简单，只需要以与正向传播相反的顺序调用各层的 backward() 函数即可。在正向传播时，中间层的神经元 h 被复制了多份，这相当于 Repeat 节点，因此在反向传播时，需要将多份梯 度累加起来。

以上就是负采样的实现的说明。

3. 改进版 word2vec 的学习

我们介绍了 Embedding 层和负采样的方法，并对他们进行了实现。现在我们用实现进行了这些改进的神经网络，并在 PTB 数据集上进行学习，以获得更加实用的单词的分布式表示。

3.1 CBOW 模型的实现

我们改进之前实现的 SimpleCBOW 类，来实现 CBOW 模型。改进之处：

• 使用 Embedding 层和 Negative Sampling Loss 层
• 将上下文部分扩展为可以处理任意的窗口大小

3.1.1 初始化

class CBOW:
    def __init__(self, vocab_size, hidden_size, window_size, corpus):
        """
        :param vocab_size: 词汇量
        :param hidden_size: 中间层的神经元个数
        :param window_size: 上下文的大小，当值为 2 时，目标词左右各 2 个，共 4 个单词成为上下文
        :param corpus: 单词 ID 列表
        """
        V, H = vocab_size, hidden_size

        # 初始化权重
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(V, H).astype('f')

        # 生成层
        self.in_layers = []
        for i in range(2 * window_size):
            layer = Embedding(W_in)  # 使用Embedding层
            self.in_layers.append(layer)
        self.ns_loss = NegativeSamplingLoss(W_out, corpus, power=0.75, sample_size=5)

        # 将所有的权重和梯度整理到列表中
        layers = self.in_layers + [self.ns_loss]
        self.params, self.grads = [], []
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads

        # 将单词的分布式表示设置为成员变量
        self.word_vecs = W_in

SimpleCBOW 中 和 形状不同， 在列方向上排列单词向量。而 CBOW 类的 和 形状相同，都在行方向上排列单词向量。这是因为 NegativeSamplingLoss 类中使用了 Embedding 层。

3.1.2 forward 和 backward

def forward(self, contexts, target):
    h = 0
    for i, layer in enumerate(self.in_layers):
        h += layer.forward(contexts[:, i])
    h *= 1 / len(self.in_layers)
    loss = self.ns_loss.forward(h, target)
    return loss

def backward(self, dout=1):
    dout = self.ns_loss.backward(dout)
    dout *= 1 / len(self.in_layers)
    for layer in self.in_layers:
        layer.backward(dout)
    return None

这里的实现只是按适当的顺序调用各个层的正向传播（或反向传播），这是对上一章的 SimpleCBOW 类的自然扩展。

不过这里的 contexts 和 target 都是单词 ID 形式，而不是 SimpleCBOW 中的 one-hot 形式：

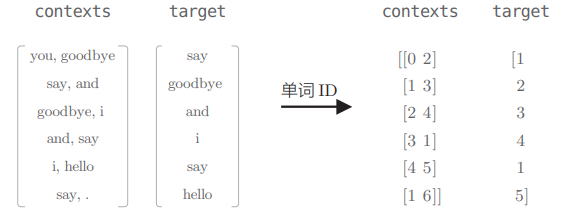
3.2 CBOW 模型的学习

最后，我们来实现 CBOW 模型的学习部分。其实只是复用一下神经网络的学习：

# 设定超参数
window_size = 5
hidden_size = 100
batch_size = 100
max_epoch = 10

# 读入数据
corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)

contexts, target = create_contexts_target(corpus, window_size)

# 生成模型等
model = CBOW(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)

# 开始学习
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()

# 保存必要数据，以便后续使用
word_vecs = model.word_vecs
params = {}
params['word_vecs'] = word_vecs.astype(np.float16)
params['word_to_id'] = word_to_id
params['id_to_word'] = id_to_word
pkl_file = 'cbow_params.pkl'  # or 'skipgram_params.pkl'
with open(pkl_file, 'wb') as f:
    pickle.dump(params, f, -1)

这次我们利用的 PTB 语料库比之前要大得多，因此学习需要很长时间。在学习结束后，取出权重（输入侧的权重），并保存在文件中以备后用，这里使用 pickle 功能进行序列化。

3.3 CBOW 模型的评价

我们来评价一下上一节学习到的单词的分布式表示。这里我们使用第 2 章中实现的 most_similar() 函数，显示几个单词的最接近的单词：

from common.util import most_similar, analogy
import pickle

pkl_file = 'cbow_params.pkl'

with open(pkl_file, 'rb') as f:
    params = pickle.load(f)
    word_vecs = params['word_vecs']
    word_to_id = params['word_to_id']
    id_to_word = params['id_to_word']

# most similar task
querys = ['you', 'year', 'car', 'toyota']
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5)

运行结果：

运行结果

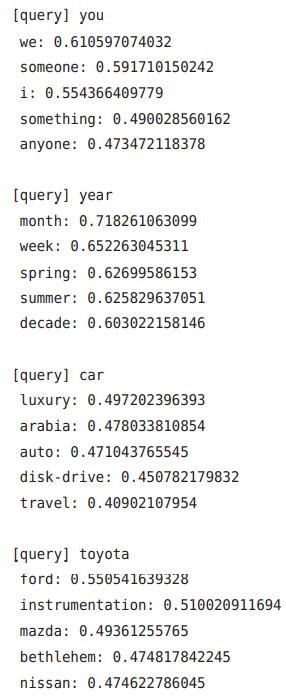
• 首先，在查询 you 的情况下，近似单词中出现了人 称代词 i（= I）和 we 等。
• 接着，查询 year，可以看到 month、week 等表示时间区间的具有相同性质的单词。
• 然后，查询 toyota，可以得到 ford、mazda 和 nissan 等表示汽车制造商的词汇。

从这些结果可以看出，由 CBOW 模型获得的单词的分布式表示具有良好的性质。

此外，由 word2vec 获得的单词的分布式表示不仅可以将近似单词聚拢在一起，还可以捕获更复杂的模式，其中一个具有代表性的例子是因“king − man + woman = queen”而出名的类推问题。使用 word2vec 的单词的分布式表示，可以通过向量的加减法来解决类推问题：

我们用函数 analogy() 封装了这部分逻辑，这样可以用如下代码来实现刚才的类推问题：

analogy('man', 'king', 'woman', word_to_id, id_to_word, word_vecs, top=5)

现在，我们来实际解决几个类推问题并查看结果：

analogy('king', 'man', 'queen', word_to_id, id_to_word, word_vecs)
analogy('take', 'took', 'go', word_to_id, id_to_word, word_vecs)
analogy('car', 'cars', 'child', word_to_id, id_to_word, word_vecs)

执行这些代码，可以得到如下结果：

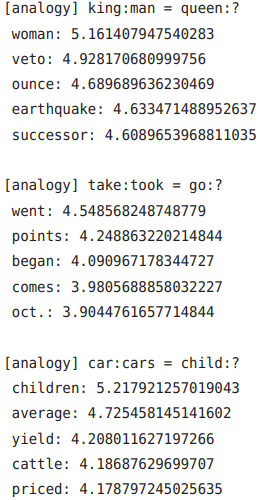
• 第 1 个问题正确回答了”woman“
• 第 2 个问题可以发现它捕获了现在时和过去时之间的模式的证据，可以解释为单词的分布式表示编码了时态相关的信息
• 第 3 个题可知，单词的单数形式和复数形式之间的模式也被正确地捕获

这里的类推问题的结果看上去非常好，不过遗憾的是，这些都是特意选出来的，实际上有很多问题都无法获得预期的结果。这是因为 PTB 数据集的规模还是比较小，增大数据集还可以大大提高类推问题的准确率。

4. word2vec 相关的其他话题

4.1 word2vec 的应用

在自然语言处理领域，单词的分布式表示之所以重要，原因就在于迁移学习。在解决自然语言处理任务时，一般不会使用 word2vec 从零开始学习单词的分布式表示，而是先在大规模语料库（Wikipedia、Google News 等文本数据）上学习，然后将学习好的分布式表示应用于某个单独的任务，这往往会有很好的效果。

单词的分布式表示的优点是可以将单词转化为固定长度的向量。另外也可以使用它来将文档（单词序列）转化为固定长度的向量。

目前，关于如何将文档转化为固定长度的向量，相关研究已经进行了很多，最简单的方法是，把文档的各个单词转化为分布式表示，然后求它们的总和。这是一种被称为 bag-of-words 的不考虑单词顺序的模型。

将单词和文档转化为固定长度的向量是非常重要的。因为如果可以将自然语言转化为向量，就可以使用常规的机器学习方法（神经网络、SVM 等）：

在上面流程中，单词的分布式表示的学习和机器学习系统的学习通常使用不同的数据集独立进行。比如，单词的分布式表示使用 Wikipedia 等通用语料库预先学习好，然后机器学习系统（SVM 等）再使用针对当前问题收集到的数据进行学习。但是，如果当前我们面对的问题存在大量的学习数据，则也可以考虑从零开始同时进行单词的分布式表示和机器学习系统的学习。

利用 word2vec 的单词的分布式表示，可以期待大多数自然语言处理任务获得精度上的提高。

4.2 单词向量的评价方法

我们简单说明分布式表示的评价方法。

在现实世界中，我们想要的一个系统往往是由多个子系统组成的。比如情感分析系统包括生成单词的分布式表示的系统（word2vec）、对特定问题进行分类的系统（SVM 等）。单词的分布式表示的学习和分类系统的学习有时可能会分开进行。如果先进行单词的分布式表示的学习，再利用这个分布式表示进行另一个机器学习系统的学习，在两个阶段学习之后才评价，会非常耗时。因此，单词的分布式表示的评价往往与实际应用分开进行，此时经常使用的评价指标有“相似度”和“类推问题”。

• 单词相似度的评价通常使用人工创建的单词相似度评价集来评估。比如 cat 和 animal 的相似度是 8，cat 与 car 是 2 .... 类似这样人工地对单词之间的相似度打分，然后，比较人给出的分数和 word2vec 给出的余弦相似度，考察它们之间的相关性。

• 类推问题的评价是指，基于诸如“king : queen = man : ?”这样的类推问题，根据正确率测量单词的分布式表示的优劣。

一个类推问题的评价结果：

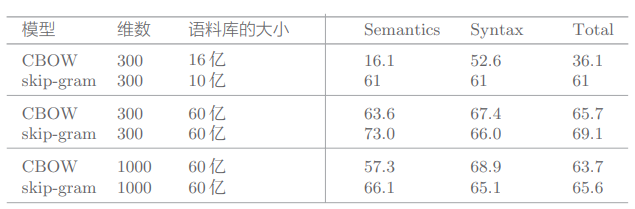
由上图可知：

• 模型不同，精度不同（根据语料库选择最佳的模型）
• 语料库越大，结果越好（始终需要大数据）
• 单词向量的维数必须适中（太大会导致精度变差）

基于类推问题可以在一定程度上衡量“是否正确理解了单词含义或语法问题”。因此，在自然语言处理的应用中，能够高精度地解决类推问题的单词的分布式表示应该可以获得好的结果。但是，单词的分布式表示的优劣对目标应用贡献多少，取决于待处理问题的具体情况，不能保证类推问题的评价高，目标应用的结果就一定好。

本章小结

我们对 CBOW 模型进行了改进，引入了 Embedding 层和负采样的方法，这一改进的背景是原先的方法随着语料库词汇量的增加，计算量也按比例增加。

利用“部分”数据而不是“全部”数据，这是本章的一个重要话题。由于计算机性能限制，仅处理对我们有用的那一小部分数据会有更好的效果。这就是负采样的思想。

关于 word2vec 的介绍也进入了尾声，word2vec 对自然语言处理领域产生了很大的影响，基于它获得的单词的分布式表示被应用在了各种自然语言处理任务中。另外，不仅限于自然语言处理，word2vec 的思想还被应用在了语音、图像和视频等领域中。理解其思想，在许多领域都能派上用场。